Компьютерное моделирование рецептуры творожного продукта «Кислинка» с растительными компонентами

Следовательно, выбор творога в качестве основного компонента животного происхождения при создании новых видов комбинированных молочно-растительных продуктов обусловлен его популярностью в традиционном рационе питания, отличными функциональными свойствами и технологичностью для комбинирования. Уже известны технологии ряда творожных изделий с добавками растительного происхождения.

Введение растительных компонентов в молочную белковую основу позволяет заменить часть животного белка растительным, значительно обогатить его минеральный состав, повысить содержание в нем витаминов, особенно водорастворимых, а также привнести в продукт пищевые волокна [1, 2].

Одним из самых безопасных наполнителей на сегодняшний день являются фруктовые и ягодные добавки. Они всегда будут популярны благодаря своему натуральному, природному вкусу. Производителю под силу сделать так, чтобы они сохраняли свои свойства: необыкновенный вкус, красивый цвет, чудесный аромат. Современные технологии делают продукты более транспортабельными, стойкими к различным условиям (например, к холоду, жаре).

В свете концепции теории сбалансированного питания задача оптимизации рецептур заключается в подборе компонентов и определении их соотношений, которые обеспечивают максимальное (в большей или меньшей степени) приближение массовых долей нутриентов к принятым эталонам. В такой постановке решение оптимизационных задач предполагает наличие априорной или экспериментально получаемой информации о массовых долях макро- и микропитательных веществ в рецептурной композиции.

При составлении рецептуры творожного продукта «Кислинка» были использованы следующие наполнители: киви, крыжовник и банан. При выборе этих наполнителей учитывались следующие критерии:

• -    в киви много калия, который незаменим для детей, страдающих аллергией; также в киви содержится много растительной клетчатки, которая отлично стимулирует работу кишечника. Этот фрукт богат витаминами С, РР, Е. Особенно ценно большое количество витамина С в киви, этот витамин помогает усвоению железа в детском организме, что является хорошей профилактикой анемии;

• -    в свежих ягодах крыжовника содержится от 5 до 15% сахаров, около 2% органических кислот, до 55% витамина С, легко усвояемые соли фосфора, кальция, железа, а в плодах с темной окраской - еще и вещества группы антоцианов, обладающие Р-витаминной активностью. Благодаря наличию пектиновых веществ ягоды крыжовника являются естественными антирадиантами, способствуют выведению из организма человека продуктов радиоактивного распада и усилению обмена веществ;

• -    в мякоти банана содержится до 80% воды, клетчатка, пектиновые вещества, улучшающие пищеварение, крахмал (7-20%), который при созревании плодов превращается в сахар, белки - до 2%, углеводы - до 25% (в основном сахароза), яблочная кислота, дубиль-

• ные и ароматические вещества, ферменты, витамины С, В1, В2, провитамин А, катехоламины. По содержанию витамина С бананы не уступают некоторым цитрусовым: в спелых плодах на 100 г мякоти находится от 8 до 12 мг этого витамина, также бананах содержатся соли кальция, магния, натрия, фосфора, железа и очень много калия. Аромат свежих плодов зависит от наличия в их мякоти сложных эфиров [3, 4, 5].

Так, компьютерное моделирование является одним из эффективных методов изучения сложных систем, а с помощью компьютерных моделей проще и удобнее исследовать и проводить вычислительные эксперименты в тех случаях, когда реальные эксперименты затруднены из-за финансовых или физических препятствий или могут дать непредсказуемый результат. Логичность и формализованность компьютерных моделей позволяет выявить основные факторы, определяющие свойства изучаемого объекта-оригинала, в частности, исследовать отклик моделируемой физической системы на изменения ее параметров и началь -ных условий [3, 5].

Среди различных моделей технологических процессов особое место занимают так называемые линейные модели , т.е. модели, где математические зависимости (равенства или неравенства) линейны относительно всех переменных величин, включенных в модель. Сущность данных задач заключается в том, чтобы из множества возможных вариантов исследуемого процесса выбрать по заданному признаку наилучший или оптимальный вариант.

Разработка общих методов их решения начата в 1939 г. русским математиком, лауреатом Нобелевской премии, академиком Л.В. Канторовичем и его учениками.

Особую важность в настоящее время приобретает решение технологических задач на базе компьютерных информационных систем с целью полноты использования составных частей ингредиентов, получение продукта высокого качества с заданными параметрами, например, с минимальной себестоимостью, максимальной энергетической ценностью продукта и др.

Сложность многокомпонентной рецептурной задачи заключается и в том, что в настоящее время используется большое количество ингредиентов (от 5 и более). Поэтому расчет рецептуры смеси продукта без использования современных компьютерных информационных технологий требует значительных затрат времени, что приводит к потере оперативности управления производством и экономической неэффективности.

Следовательно, компьютерное моделирование помогает в проведении серии вычислительных экспериментов на компьютере, целью которых является анализ, интерпретация и сопоставление результатов моделирования с реальным поведением изучаемого объекта и, при необходимости, последующее уточнение модели и т.д. Задача производителя заключается лишь в том, чтобы выбрать оптимальный вариант.

Использование компьютерного моделирования для составления рецептур с многокомпонентным составом продукта позволит получить снижение себестоимости разрабатываемого продукта без потери его качественных показателей.

Рассмотрим пример оптимизации рецептуры многокомпонентного творожного продукта «Кислинка» с помощью компьютерного моделирования.

Формулируем задачу: Требуется разработать рецептуру творожного продукта «Кислинка». На 100 кг смеси творожного продукта добавляется: творога жирного (18%) - не менее 80,0 кг; киви - не менее 3,0 кг; крыжовника - не менее 1,0 кг; банана - 1,0; масла сладкосливочного несоленого - не менее 2 кг; ванилина - 0,05 кг.

В табл. 1 представлена информационная матрица данных для оптимизации рецептуры продукта, которая включает в себя пять элементарных блоков: ингредиенты, химический состав ингредиентов, оптовые цены, требования стандарта проектируемого продукта, индексированные переменные (обозначенные через Х).

На основании информационной матрицы данных (табл. 1) формируем систему линейных алгебраических балансовых управлений по белку, жиру, углеводам, воде и массе творожного продукта (табл. 2).

Таблица 1

Информационная матрица данных для оптимизации рецептур творожного продукта «Кислинка»

Ингредиенты	Х	Масса, кг	Массовая доля,%				Цена, руб./кг
			жира	белка	углеводов	воды
Творог жирный	х1		18,0	14,0	2,8	65,2	90,00
Киви	х2		0,4	0,8	8,1	83,8	50,00
Крыжовник	х3		0,2	0,7	9,1	84,7	150,00
Банан	х4		0,5	1,5	21	74	30,00
Масло сладкосливочное несоленое	х5		72,5	0,8	1,3	25,0	150,00
Ванилин	х6		0,0	0,0	0,0	0,0	240,00
Сахар	х		0	0,0	99,8	0,1	30,00

Таблица 2

Система балансовых линейных алгебраических уравнений

Баланс	Уравнения и ограничения
Белок	0,14х1 + 0,008х2 + 0,007х3 + 0,015х4 + 0,008
Жир	0,18х1 + 0,004х2 + 0,002х3 + 0,005х4 + 0,725х5
Углеводы	0,028х1 + 0,081х2 + 0,091х3 + 0,216х4 + 0,13х5 + х6 + 0,998х7
Вода	0,652х1 + 0,838х2 + 0,847х3 + 0,74х4 + 0,25х5 + х6 + 0,001х7
Ванилин	Х7 = 0,05
Масса творожного продукта	Х1 + х2 + х3 + х4 + х5 + х6 + 0,7х =_100,00

В свете концепции теории сбалансированного питания задача оптимизации рецептур заключается в подборе компонентов и в определении их соотношений, которые обеспечивают максимальное (в большей или меньшей степени) приближение массовых долей нутриентов к принятым эталонам. В такой постановке решение оптимизационных задач предполагает наличие априорной или экспериментально получаемой информации о массовых долях макро- и микропитательных веществ в рецептурной композиции.

С учетом многообразия вариантов подбора исходных рецептурных ингредиентов и их соотношений между собой экспериментальный путь получения упомянутой выше информации представляется менее выгодным. В связи с этим, а также учитывая предположение, что все виды механической обработки сырья не нарушают позиционного принципа в отношении биологически важных питательных веществ исходных ингредиентов для получения расчетной информации о массовых долях основных питательных веществ, может быть использована следующая формула, описывающая уравнения материального баланса:

n

E Xi ' Si

,

S = i=1________ см        n

E Xi

I = 1

где S см – массовая доля конкретного макро- или микропитательного вещества в рецептурной смеси, доля единицы или %;

Х I – массовая доля i-го компонента в рецептурной смеси, доля единицы или %;

S I – массовая доля конкретного макро- или микропитательного вещества в i-ом компоненте, доля единицы или %.

В качестве критерия оптимизации (функционала) может быть выбрана себестоимость творожного продукта, энергетическая ценность, массовая доля жира, белка и содержание углеводов. Например, выражение функции цели – минимальная себестоимость продукта «Кис- линка» – запишется в виде:

90 · х1 + 50 · х2 + 150 · х3 + 30 · х4 + 150 · х5 + 240 · х6 + 30 · х7 → min.

Минимизация энергетической ценности творожного продукта имеет вид:

n

ф ( х ) = Z Ei ■ X i ^ min ,                               (2)

i = 1

где х i = ( х 1 , х 2 , ..., х 8 ) – вектор неизвестных искомых;,

Е i – энергетическая ценность i-го ингредиента составляющего продукта, ккал.

Энергетическая ценность каждого ингредиента в рецептуре продукта рассчитывалась по формуле

Е i = 9 Ж i + 4 Б i + 3,75 У i , ккал                              (3)

где Ж i – массовая доля жира i-го ингредиента, %;

Б i – массовая доля белка i-го ингредиента, %;

У i – массовая доля углеводов i-го ингредиента, %.

Реализация поставленной задачи решалась с помощью компьютерного моделирования творожного продукта с фруктово-ягодными добавками, с использованием стандартной офисной программы Microsoft Excel с надстройкой «Поиск решения» (рисунок).

Последовательность расчета заключается в следующем. В ячейке С11 вычисляем суммарную массу всех компонентов смеси мороженого по следующей формуле: = СУММ(С3:С9).

В строке 14 осуществляем ввод балансовых уравнений, в ячейках с D14 по G14 вычисляют массовые доли жира, белка, углеводов и воды в 100 кг творожного продукта.

Например, формула в ячейке D14 будет следующая:

= СУММПРОИЗВ($C3:$C$9;D3:D9)/100.

Эту формулу копируем в ячейки E14, F14, G14.

В ячейке H13 вычисляется себестоимость 100 кг творожного продукта как сумма произведений массы отдельного вида сырья на его цену.

Формула в ячейке Н13 имеет вид:

= СУММПРОИЗВ(С3:С9;Н3:Н9).

В строке «Стандарт продукта» (строка 12) приводится химический состав продукта, содержание жира, белка, углеводов, воды. После ввода исходной таблицы и записи формул запускают функцию Поиск решений ( Меню→ Сервис → Поиск решений ). На экране появится диалоговое окно «Поиск решений», в котором необходимо выбрать ячейку целевой функции – например, минимальная себестоимость. Выбираем изменяющиеся ячейки – это ячейки, содержащие массы отдельных видов сырья (С3:С9).

Затем добавляют ограничения: все ячейки, содержащие массы отдельных видов ингредиентов, должны быть больше или равны нулю (С3:С9 > = 0).

После ввода всех параметров нажимают кнопку Выполнить в окне «Поиск решений» (рисунок).

С учетом принятых обозначений рассчитанная рецептура при выработке 100 кг творожного продукта приведена в табл. 3.

Вариация рецептур позволяет определить минимальную энергетическую ценность творожного продукта с растительными компонентами. Так, рецептура под номером 1 имеет энергетическую ценность 864,96 кДж и меньше рецептуры под номером 3 (1176,86) на 311,9 кДж, при этом разница в себестоимости приведенных рецептур составляет: 9664,50 – 8469,50 = 1195,0 руб. при выработке 100 кг продукта.

Проектирование многокомпонентных молочных продуктов с использованием современных компьютерных технологий позволяет рационально использовать молочные и фруктово-ягодные компоненты, расширить ассортиментную линейку творожных продуктов.

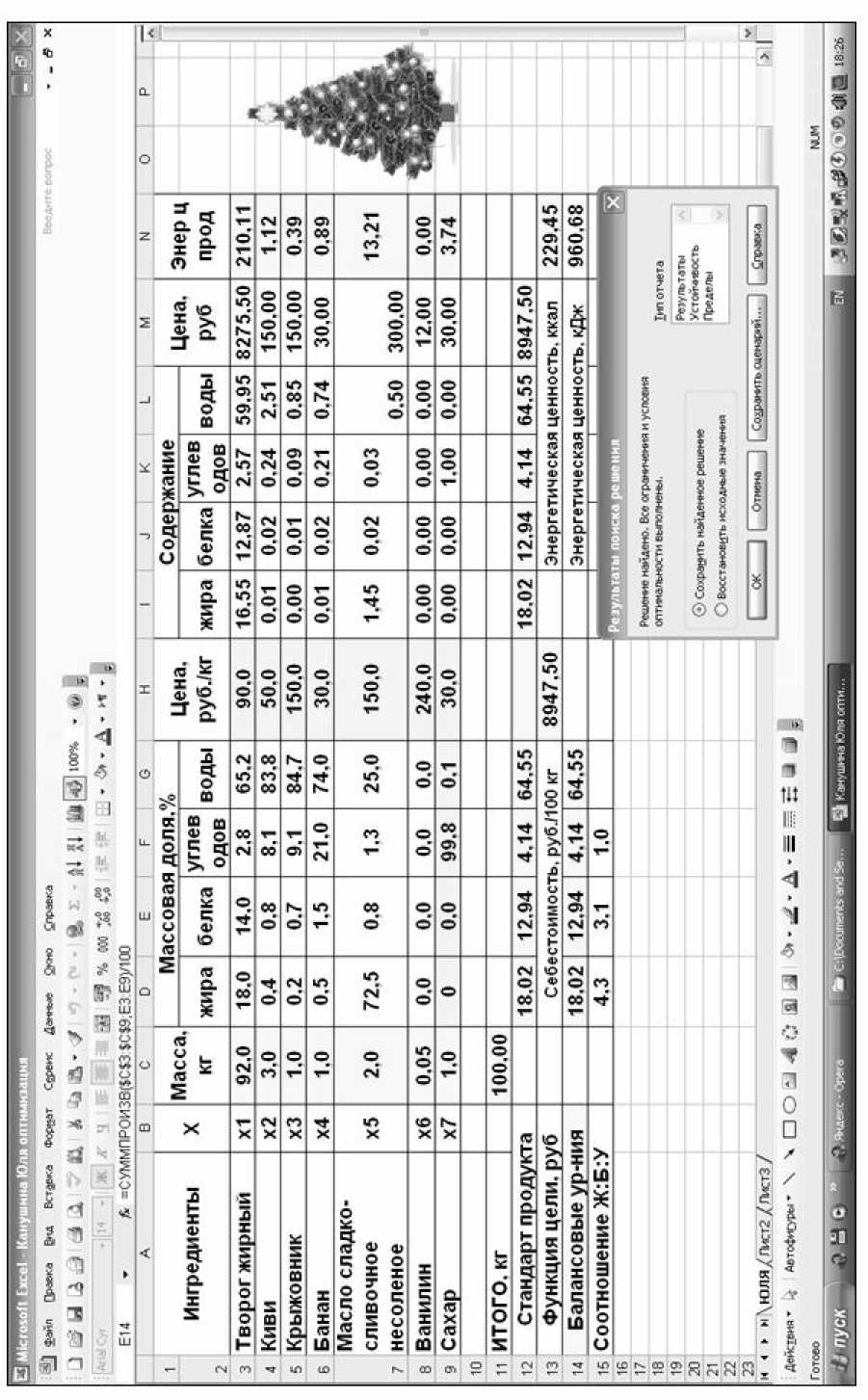
Фрагмент оптимизации рецептуры по критерию максимального содержания белка в творожном продукте «Кислинка» с фруктово-ягодными наполнителями в системе Microsoft EXCEL

Таблица 3

Ингредиенты	Индекс, Х I	Варианты рецептур, расход ингредиентов? кг, на 100 кг (без учета потерь)
		1	2	3	4	5
Творог жирный	Х 1	80,0	92,0	80,0	80,0	80,0
Киви	Х 2	15,0	3,0	3,0	3,0	3,0
Крыжовник	Х 3	1,1	1,0	1,0	1,0	1,0
Банан	Х 4	1,1	1,0	1,0	7,0	1,0
Масло сладкосливочное	Х 5	2,0	2,0	14,0	2,0	2,0
Ванилин	Х 6	0,05	0,05	0,05	0,05	0,05
Сахар	Х 7	1,0	1,0	1,0	7,0	13,0
Энергетическая ценность, кДж		864,96	960,68	1176,86	962,31	1033,60
Себестоимость, руб.		8469,50	8947,50	9664,50	8230,50	8230,50
Массовая доля, %
жира		15,92	18,02	24,53	15,90	15,87
белка		11,36	12,94	11,36	11,35	11,26
углеводов		4,78	4,14	3,96	11,03	15,73
Соотношение Ж:Б:У		3,3:2,4:1,0	4,3:3,1:1,0	6,2:2,9:1,0	1,4:1,0:1,0	1,0:0,7:1,0

Варианты рецептур творожной массы «Кислинка»