Комплексная онтология нейродинамической системы в современной теории катастроф: структурная и функциональная конфигурация

Развитие теоретических принципов построения нейродинамических систем ( ND -систем) в рамках комплексной онтологии осуществляется на основе интеллектуальных технологий XXI века [1-5]. Особенностью онтологии ND -системы является интеграция вычислительных технологий, организованных на основе нейронечёткого и нейроэволюционного моделирования. Существенная роль в реализации онтологических принципов структурной и функциональной конфигурации ND -системы на основе методов современной теории катастроф принадлежит фрактальной геометрии и формальному концептуальному анализу. Онтология, отображающая графическую интерпретацию физических закономерностей при исследовании динамики взаимодействия сложного динамического объекта (ДО) с внешней средой формализуется на базе фрактальных структур ND -системы [3]. Рассматриваемая онтология ND -системы представляет собой структуру S ( G ), моделирующую процессы развития угрожающих ситуаций в рамках парадигмы обработки информации в мультипроцессорной вычислительной среде [3]. Возникновение предаварийных и аварийных ситуаций и механизмов управления изменениями в структуре программных модулей бортовой интеллектуальной системы (ИС) обеспечения безопасности мореплавания описывается с помощью онтологии потоков событий в раках концепции Workflow [1,2].

Концептуальная модель преобразования информации в ND -системе, обеспечивающей функционировании ИС в сложной динамической среде, имеет вид:

• (1)             5 ( U ) = ( F ( Com ) : { Т ( t , т ) х X ( KB ) х Q ( V , W )} ^ Y ( R )

где 5 ( U) — множество стратегий управления; Х ( KB ) — множество элементов оперативной базы данных (БД); Т ( t , т ) — множество моментов времени, определяющих модель развития угрожающих ситуаций; Q ( V , W) — множество значений вектора входных воздействий (состояние внешней среды - ветроволновые возмущения); { Т ( t , т ) х X ( KB ) х Q ( V , W) } — множество закономерностей в данных; Y ( R ) — множество правил обобщения информации; F ( Com ) — множество элементов, реализующих принцип конкуренции; т - интервал квазистационарности.

Обратная алгоритмическая связь в концептуальной модели (1) используется для моделирования управляющей деятельности оператора по способам формирования управленческих воздействий в зависимости от критичности возникающих ситуаций. Обеспечение взаимодействия оператора с ИС при поддержке принятия решений реализуется на основе критериев эффективности. Принципом обратной алгоритмической связи в ИС является разность энтропий системы до и после получения информации, что уменьшает неопределенность в оценке и анализе текущего состояния ДО и неоднозначность в выборе способов формирования управляющих воздействий в зависимости от критичности возникающих ситуаций.

Организация ND -системы осуществляется в рамках концепции современной теории катастроф [3]. Конфигурации системы представляется фрактальным графом

• (2)    G ( F r ) = ( V ( E , U ) , A ( E , C ))

формализующим события ( V ( Е, U), описывающие действия в системе, и условия А ( E, С ) в виде логического описания ее состояния. Как следует из этого представления, ND -система обеспечивает обработку потока информации, связанного с состояниями ДО и условиями их описания в процессе эволюции в нестационарной динамической среде.

На рисунке 1 приведена формальная модель функционирования ND -системы, осуществляемого управляющим модулем, взаимосвязанным с программной средой бортовой ИС контроля чрезвычайных ситуаций (показаны только база знаний и база данных этой системы).

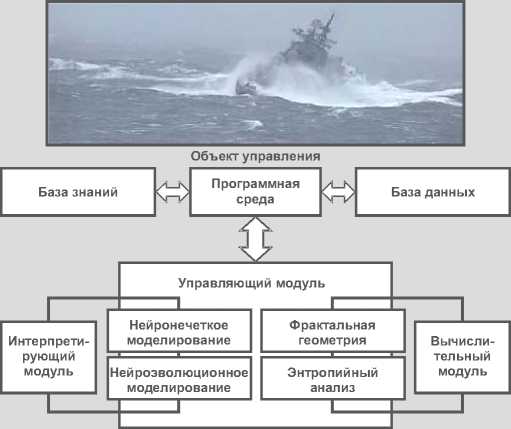
Рисунок 1 - Концептуальная модель онтологии нейродинамической системы в рамках интегрированного вычислительного комплекса контроля поведения сложных динамических объектов

Функциональный блок ND -системы содержит интерпретирующий и вычислительный модули, обеспечивающие нейронечёткое и нейроэволюционное моделирование с использованием фрактальной геометрии и энтропийного анализа. Интеграция указанных компонент реализована в рамках динамической модели катастроф, позволяющей формализовать процессы обработки информации на основе достижений интеллектуальных технологий и высокопроизводительных средств [3].

В рамках представленной концептуальной модели формализуются процессы структурной и функциональной конфигурации ND -системы на основе аппарата знаний логической системы, организованной на базе синергетической теории управления [5] и когнитивной парадигмы [3]. Методы и модели динамической базы знаний (БЗ) построены с использованием принципа сложности и концепции минимальной длины описания [3].

1 Комплексная онтология, определяющая формальный аппарат стрyктурного и параметрического синтеза ND–системы

Формальную модель комплексной онтологии информационной среды M ( 5 ) ND -системы, обеспечивающей анализ и прогноз чрезвычайных ситуаций при функционировании бортовой ИС контроля поведения морского ДО, можно представить в виде обобщенной структуры [3]:

• (3)    M ( 5 ) = ( F ( 5 ) , 5 ( г ) , B ( AR ) , D ( Q . W . V ) . U ( PC )) ,

где F ( 5 ) - функциональные компоненты ND -системы; 5 ( t ) - исследуемые ситуации; B ( AR ) -динамическая база знаний; D ( Q , W , V ) - обобщенная база данных; U ( PC ) - управляющий программный комплекс.

Функциональными компонентами F ( CS) являются исполнительные модули прикладных систем и служебные модули, обеспечивающие совместную работу объединяемых систем. Эти модули взаимодействуют с динамической БЗ B ( AR ) и обобщенной БД D ( Q . W , V ). Управляющий программный комплекс U ( PC) обеспечивает функционирование системы M ( 5 ) в сложной динамической среде. Обобщенная БД D ( Q . W , V) формируется в соответствии с общими принципами построения БД бортовых ИС и содержит данные Q о характеристиках ДО, волнения W и ветра V . Структура управления программными системами представлена на основе сетевых моделей упорядочения событий в рамках фрактальной геометрии в соответствии с логикой системы и потоком информации в текущей ситуации.

Рисунок 2 показывает основные операции, выполняемые в процессе функционирования бортовой ИС в рамках парадигмы обработки информации в мультипроцессорной вычислительной среде. Реализация этих операции осуществляется на основе комплексной онтологии, позволяющей формализовать описание компонент системы на уровне структурной и функциональной конфигурации. Принципиальным достоинством такой технологии является представление эволюции ДО на интервале реализации [ t о , t k ] в виде фрактальных структур, а интерпретации динамики взаимодействия - с помощью энтропийного анализа. В результате достигается простота и наглядность отображения процесса развития чрезвычайной ситуации в сложной динамической среде [3].

Рассматриваемые в ИС контроля чрезвычайных ситуаций текущие фракталы отображают эволюцию ДО в виде эллипсоидальных структур

• (4)    g ( v ( E ) , a ( E )) e G V ( E ). A ( E )),

в виде последовательности конфигураций g 1 ( F R ). „.. g N ( F R ) на стадии эволюции динамической системы, определяющей движение фрактала, представленного сечениями эллипсоида в плоскостях XY и YZ при стабилизации системы (движение к целевому аттрактору) и при потере устойчивости (возникновение катастрофы).

РЕАЛИЗАЦИЯ РЕЗУЛЬТАТОВ МОДЕЛИРОВАНИЯ ДИНАМИКИ СУДНА НА ОСНОВЕ КОНЦЕПЦИИ КЛИМАТИЧЕСКИХ СПЕКТРОВ

Виртуальное моделирование задачи		Генерация альтернатив и выбор решения
Когнитивное моделирование задачи		Функция и модель выбора, метод эталонов

Рисунок 2 - Комплексная онтология, определяющая формальный аппарат преобразования информации в рамках парадигмы [3]

На основе текущей конфигурации семейства фракталов фиксируются начальное g ₀( F R ) и конечное g N ( F R ) состояния системы «ДО - внешняя среда» в зависимости от интерпретации в плоскостях XY и YZ сечения эллипсоида. Система развивается на временном интервале [ t ₀, t k ], которому сопоставляется последовательность дискретных состояний

• (5)                                      S ( t ) е S [ t о , t k ]

формализуемых в рамках гипотезы квазистационарности [3] теории нелинейных динамических систем.

2 Онтологические принципы интерпретация динамических ситуацийпри функционировании ND-системы

Онтологические принципы организации процессов обработки информации в ND -системе S ( G ) контроля поведения ДО реализуются на основе сервисно-ориентированной архитектуры SOA, а конфигурация программного обеспечения и вычислительных средств - в рамках «облачных» CLOUD-вычислений [1,2]. Методы управления в системе «ДО - внешняя среда» ориентированы на обеспечение функционирования в условиях непрерывного изменения динамики объекта и внешней среды. Адаптация системы обеспечивается с помощью механизмов нечёткого управления, определяющих конфигурацию «вход-выход», при этом обратная связь может быть отрицательной при стабилизации системы в бассейне аттрактора, или положительной, ведущей к бифуркации, нестабильности и хаосу [3].

На рисунке 3 даётся содержательная интерпретации аттракторных множеств, формируемых в процессе движения системы к целевому аттрактору. Здесь выделены характерные ситуации возникновения аттракторных множеств при устойчивом и неустойчивом состоянии системы в виде предельных циклов и фокусов.

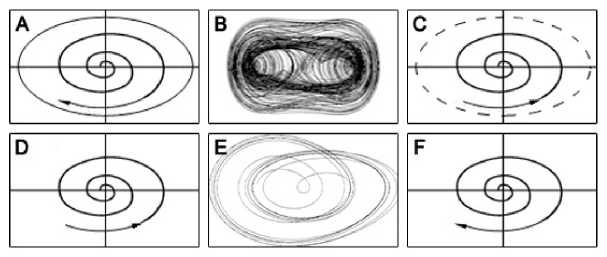
Рисунок 3 - Структуры аттракторных множеств, характеризующие эволюцию системы:

А, С - устойчивый и неустойчивый предельные циклы; D, F - устойчивый и неустойчивый фокусы;

В - сложный стохастический аттрактор; Е - простой стохастический аттрактор

Реализация событий на интервале времени [ t о , t k ] осуществляется с помощью логических операций нечёткой системы знаний. Последовательность событий в процессе эволюции ДО реализуется с помощью правил Р 1 , „., P N , которым соответствуют алгоритмы A 1 ,., A N системы S ( G ), так что фрактал G 1 ( F R ) преобразуется в G ₂( F R ) и т.д. Эта последовательность определяется фиксированными положениями ДО G 1 , „., G N в процессе развития текущей ситуации:

• (6)                                 S ( t ) = ( Р , ,..., P n , A 1 ,..., A n )

Таким образом, множество фракталов характеризуется множеством упорядоченных правил Р 1 , .., P N и алгоритмов обработки информации А 1 , .., A N , с помощью которых обеспечивается оперативный контроль взаимодействия ДО с внешней средой.

В основу формального аппарата динамики взаимодействия положен теоретический принцип динамической модели катастроф, формализующий движение системы в процессе эволюции. Как следует из этого принципа, эволюция системы «ДО-внешняя среда» интерпретируется в виде двух предельных случаев взаимодействия:

• (7)            ^ф( Inf ) : n⁽ W ^{) —}^ ... -^ П⁽ Stab ) ;

• (8)          ^ W ^{) —}^... — и ^— n⁽ Cat )

где ^ ( W) - области, характеризующие состояния системы «ДО-внешняя среда» и заданные на основе фрактальной геометрии; ^ ( Stab ) - область притяжения, определяющая движение ДО к целевому аттрактору; ^ ( Cat ) - область потери устойчивости (возникновение катастрофы), [ U 1( t ), ., U m ( t )] и [ U 1( t ), ., U n ( t )] - управляющие воздействия для рассматриваемых случаев эволюции при эффективной и недостаточно эффективной интеллектуальной поддержке, когда не удается реализовать мероприятия по обеспечению безопасности, вырабатываемые ИС.

На рисунке 4 даётся содержательная интерпретация эволюции ДО, представленной на основе фрактальной геометрии в виде эллипса на интервале времени [ 1 ₀, t n ].

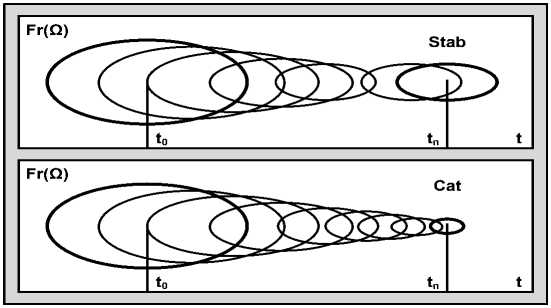
Рисунок 4 - Фрактальная интерпретация эволюции динамического объекта на интервале реализации

Стадия стабильного Stab развития ND -системы S ( G ) определяет движение системы «ДО-внешняя среда» к целевому аттрактору. В этой ситуации система остается в состоянии, близком к равновесному, а ее организация не претерпевает значительных изменений. При стабильном состоянии воздействия внешних возмущений ( V , W) на систему описываются потоковой нагрузкой, изменяющей фрактальную структуру F R ( ^ ) графа в зависимости от внешних факторов. Движение к целевому аттрактору при таком состоянии ND -системы определяется конфигурацией [3]:

• (9)    S ( G , Attr ) ^ Stab ( F R ).

Стадия критического состояния (возникновение катастрофы) характеризуется выходом исследуемых параметров ND -системы из заданного диапазона и возникновению бифуркаций - потери устойчивости ДО в условиях перехода от угрожающей ситуации к предаварийной и аварийной ситуациям, что связанно с формированием альтернативных вариантов ее организации. Такты системы в этом случае определяют процесс самоорганизации ( SO ) фрактальной структуры в условиях непрерывного изменения динамики объекта и внешней среды. Структура ND -системы при формировании катастрофы характеризуется условием:

• (10)    S ( G , SO ) ^ Cap ( F R )

Формирование сложных конфигураций фрактального представления G ( V ( Е) , А ( E) ) осуществляется путем построения отображений с различной интерпретацией потока информации. Фрактальная геометрия - эффективный класс алгебраических преобразований, используемых при функционировании ИС [4]. Модели современной теории катастроф позволяют сформировать простой и легко интерпретируемый геометрический образ, представляющий эволюцию текущей ситуации в сложной динамической среде [3].

Реализация ND -системы на основе принципа конкуренции осуществляется в соответствии со следующей цепочкой преобразований:

• (11)    СР ( Cat ) ^ { G ( F r ), S ( C m )} ^ ( AA ) ^ R ( CT) ,

где G ( F R ) - модель ND -системы, интегрирующая нейронечёткую и нейроэволюционную структуры; S ( C M ) - стандартная модель, построенная на основе модифицированного уравнения Матье и метода функционала действия [3]; ( AA ) - операция анализа альтернатив (функция интерпретации); R ( CT ) - результат выбора вычислительной технологии.

Используя структуру (11) в зависимости от особенностей взаимодействия ДО с внешней средой, можно выбирать эффективные методы оценки и прогноза чрезвычайных ситуаций и вырабатывать практические рекомендации по обеспечению безопасности исследуемого ДО. Моделирование процессов самоорганизации осуществляется на основе синергетической па- радигмы [5], позволяющей формализовать динамику фрактального ядра системы FR(G) в соответствии с принципами «расширения-сжатия». Интерпретация этого принципа сводится к оценке отношения

RE 1 = dist (n )/ d (XC, YC), где dist(n) - расстояние между ближайшими кластерами, объединяемыми на n-ом шаге, а ХС и Yc - центры кластеров. Соотношение (12) позволяет выделить следующие представления:

• (13)        dist ( n )/ d ( X C , Y C ) >  1; (растяжение);

• (14)       djd ( X C , Y C ) < 1- (сжатие).

Таким образом, для моделирования стадии перехода в новое состояние необходимо реализовать перестройку ND -системы в условиях бифуркации. Наиболее перспективным подходом при исследовании процессов самоорганизации в условиях неопределенности и многообразия альтернатив является использование деревьев решений [3].

3 Онтологические принципы интерпретации аксиоматики динамической структуры ситуаций ND-системы

Общие понятия аксиоматики исследуемой предметной области специфичны в каждой прикладной онтологии. Применительно к рассматриваемой проблеме аксиоматическое представление знаний при формализации информации на основе комплексной онтологии предусматривает использование следующих аксиом (рисунок 5).

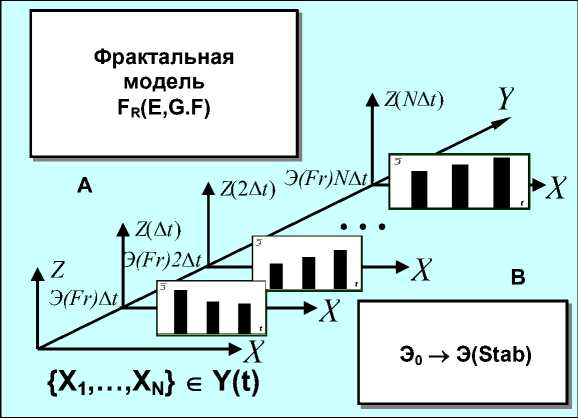
Рисунок 5 - Диаграмма, отображающая моделирование динамики ND -системы: А - модель фрактальной структуры F_R ( E , G , F) : эллиптическая, графовая, кластер Фибоначчи;

В - энтропия процесса стабилизации ситуации; Э₀ ^ Э( Stab ); Э( Fr ) А t , Э( Fr )2 А t , ..., Э( Fr ) N A t - временная последовательность, отображающая потерю устойчивости движения;

символы 1, 2, ..., N фиксируют текущее время развития ситуации на интервале прогнозирования

Аксиомы идентификации. Назначением аксиом идентификации является описание всех типов переменных и отношений, определяющих область топологической структуры ^Str ):

• (15)                      Axiom ( Ident ) = <  Var , Rel >  e ^Str ),

где Var , Rel - переменные задачи и отношения между ними.

Если объект управления описывается множеством параметров Х = { Х i , „., X N }, то требуется находить или уточнять значения части параметров. При этом каждый из параметров характеризуется определенным интервалом значений, с помощью которого задаются известные параметры и ограничения в задачах оптимизации.

Аксиомы планирования. В основе вычислений топологических объектов в области эволюции фазового пространства лежит свойство интервальной арифметики, позволяющее осуществить сходимость итеративной процедуры вычислений интервальных значений параметров к некоторым локализующим интервалам, содержащим требуемые решения.

• (16)    Axiom ( Plan ) = <  Evol ( Ph ), Int ( Cal) >,

где Evol ( Ph ) - область эволюции фазового пространства, Int ( Cal) - процедуры интервальной арифметики.

Для осуществления итеративной процедуры вводятся аксиомы планирования, задающие правила (порядок и условия корректности) вычислений.

Аксиомы вычислений. С помощью аксиом вычислений задаются правила вычисления отношений в области эволюции фазового пространства. Каждое отношение r i = r i ( Y i ) связывает некоторое множество параметров Y i и используется для вычисления неизвестных значений параметров Y i ^вых с Y i , связанных отношением по известным значениям параметров Y i ^вх с Y i . Аксиомы вычислений преобразования фазового пространства включают также аксиомы оптимизации.

• (17)    Axiom ( Calcul) = <  Rule ( Cal), Axiom ( Opt ) >, где Rule ( Cal) - правила вычислений; Axiom ( Opt ) - аксиомы оптимизации.

В отличие от аксиом идентификации, вычисления и планирования, эти аксиомы позволяют давать ответы на поставленные прямые и обратные вопросы при решении задач поиска оптимальных решений. Аксиомы оптимизации содержатся в каждом дереве классификации концептов формальной системы и представляются в виде таблиц логических аксиом ( Logical Axioms Table ). Структура таблиц включает имя аксиомы, описание, концепт, ссылочные атрибуты, переменные и определения.

Аксиоматическое представление знаний в ND -системе позволяет осуществлять поддержку процедур нейронечёткого и нейроэволюционного моделирования при интерпретации поведения ДО в процессе эволюции в сложной динамической среде. На рисунке 5 представлена фрактальная модель динамики ND -системы на основе энтропийного подхода.

Таким образом, сформулированные условия и их реализация в рамках динамической модели катастроф позволяют представить онтологию компонент интеллектуальной поддержки оператора бортовой ИС при интерпретации текущих ситуаций. Разработанные на основе такой формализации модели онтологии аналитической и геометрической компонент рассматриваются как составляющие общей проблемы онтологии исследуемой предметной области и определяются критерием истинности C R ( True ) с учетом требований полноты Dem ( Full ) и непротиворечивости Dem ( Non-Contr ) сформулированных аксиом и правил вывода:

• (18)    Ont ( SAU) = <  C_R ( True ) [ Dem ( Full), Dem ( Non-Contr )] >.

В результате проведенного исследования определена онтология предметной области с обоснованной структурой и содержанием. Формальное описание интегрированной системы знаний S = { S i | i = I, „., N} в ND -системе можно представить на основе следующих онтологий:

• (19)    Ont(NET) ^ < Ont(CONSEPT), Ont(CONNECT) >,

где Ont ( CONSEPT ) - множество понятий, обозначающих исследуемые процессы в динамических сценах (задачи интерпретации); Ont ( CONNECT) - множество связей между понятиями.

На основе представления (19) сформулирована концептуальная модель комплексной онтологии компонент модели катастроф при интерпретации текущих ситуаций:

• (20)               Ont(Com) = < Ont(A), Ont(G) > ;

• (21)               Ont ( A ) = <  Ont ( 5 ), Ont ( H) , Ont ( Syn ), Ont ( NF) , Ont ( GA ) >,

• (22)               Ont(G) = < Ont(Im), Ont(Cog), Ont(Vis)> ,

где аналитическая компонента Ont ( A ) включает онтологии, формализующие стохастические Ont ( S ) и хаотические Ont ( H ) системы, синергетическую парадигму Ont ( Syn ), нейронечёткие системы Ont ( NF) и эволюционное моделирование Ont ( GA ), а геометрическая интерпретация Ont(G) - имитационное Ont ( Im ), когнитивное моделирование Ont ( Cog ) и визуализацию Ont ( Vis ) динамических сцен.

Проверка адекватности модели онтологии на основе приведённых выше утверждений сводится к оценке корректности процедур формализации знаний динамической среды методами современной теории катастроф, определяющей объекты и отношения предметной области.

Заключение

Модель онтологической системы ND -моделирования, определяющей функционирование динамической базы знаний ИС, позволяет описывать онтологии на разных уровнях абстракции. На основе заданной предметной области реализуется интеллектуальная технология, позволяющая сформулировать общий подход к формализации знаний ИС управления и принятия решений с использованием онтологической системы. Формализация комплексной онтологии компонент системы интеллектуальной поддержки оператора ИС состоит в формальном описании интегрированной ND -системы на основе методов концептуализации знания. В результате такой интеграции реализуется структура множеств объектов и понятий, знаний и связей между ними в рамках современной теории катастроф [3].

Критерий функциональной полноты нейронечёткой и нейроэволюционной компонент нейродинамической системы зависит от класса решаемых задач и требует определения глубины их детализации. Формальная постановка задач, решаемых с помощью указанных компонент в заданной предметной области, позволяет выделить особенности текущей ситуации, моделирование которых является необходимым и достаточным для интерпретации текущих ситуаций на основе аналитической и геометрической компонент.