Комплексные представления для расчета механических систем при гармонических процессах

Традиционный расчет механизмов при вынужденных колебаниях зачастую представляет собой непростую задачу [1–3].

Чаще всего расчетчиков интересуют установившиеся режимы колебаний [4–6].

Целью работы является значительное упрощение вычислений путем замены необходимости решения дифференциальных уравнений на алгебраические методы. Подобный подход широко используется в электротехнике.

Схема параллельного соединения

Скорость элементов механической системы одинаковая (рис. 1):

v = V sin юt.(1)

При этом силы отличаются: dv f = m   = mю V cos юt,(2)

m dt

k fk = -kx = k vdt = -  V cos юt,(3)

ю

f

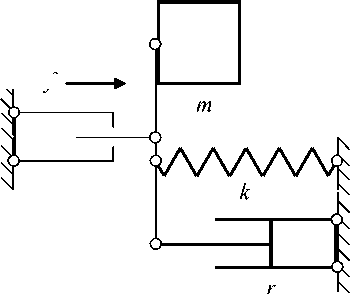
Рис. 1. Схема параллельного соединения fr = rv = rV sin юt.(4)

Результирующая сила:

f = f m + f k + f_r =

k I                       .

m ю-- I cos ю t + r sin ю t mJ

k x = m ю.

= V

= V

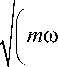
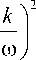
+ r²

( m ю- k /ю ) cos ю t

Если x = 0 , то ю = ^ к/m - классическое

I

m ю- к/ ю ) 2

+ r²

+

r sin ю t

+ ।          2 = ■

( m ю- к/ ю ) + r ²

Удобно ввести обозначение , m ю- к/ ю ф = arctg--------- r

выражение, полученное значительно проще классического решения. При этом происходит резонанс сил [10]. При r = 0 , z = 0 . Механизм не препятствует источнику колебаний.

По аналогии с электротехникой r – механический резистанс (resistance).

Комплексное описание для параллельной схемы соединения

При этом f = V(mmю-к/ю)2 + r2 (sinФcosюt +

+ cos p sin ю t ) =

= V ( m m ю- к/ ю ) 2 + r ² sin( ю t + ф ) = F sin( ю t + ф ) .

(6) Это классическое выражение (результат решения дифференциального уравнения).

В рассматриваемом случае необходимость в дифференциальном уравнении не возникает.

Амплитуда результирующей силы:

F = Vz ,                (7)

z = ^(m ю- к/ ю ) 2 + r ² ( кг • с ^.      (8)

Первая (максвелловская) система механо-электрических аналогий имеет вид:

• -    V ^ I (скорость ^ ток),

• -    F ^ U (сила ^ напряжение),

• -    m ^ L (масса ^ индуктивность),

• -    к ^ 1 C (коэффициент упругости ^

величина обратная емкости),

• -    r ^ R (коэффициент вязкого сопротивления ^ сопротивление).

Американский физик Вебстер дополнил эти аналогии:

• -    ю m ^ ю L ( инертный реактанс ^ индуктивное сопротивление) [7–9 ] ,

• -    к/ ю^ 1/( ю C ) (упругий реактанс ^ емкостное сопротивление).

Учитывая приведенные механо-электрические аналогии, формула (7) является аналогом известного закона Ома

U = IZ .

здесь Z = ^[ ю L - 1( ю C ) ] 2 + R ² - сопротивление. Таким образом, формула (8) – это механический импеданс (impedance).

Соответственно этому механический реактанс (reactance):

Синусоидальная величина имеет следующую форму записи:

a = A sin( ю t + ф ) = Im ^ Ae' ^{( ю} t ^{+ф )} ^ .

Здесь Ae ⁽ “ t ^{+ф )} - комплексный вектор.

Такие векторы, как правило, записыва ют для момента t = 0. В соответствии с этим

Ae'(ю0+ф) = Ae'ф = A принято считать комплексной амплитудой.

Формула (1), таким образом, имеет следующий вариант записи:

v = V sin ю t = Im( Ve ' “ t ) ,

•

V = Ve ' ⁰ .

Из выражения (2) следует, что v отстает по фазе от f_m на п/2 .Таким образом,

• •              •    ' ^-           •

F m = m ю Ve ² = x m V .

' - x_tn = ю me ² = ' ю m .           (9)

Это инертный реактанс в комплексной записи.

Несинусоидальные величины в комплексном представлении подчеркивают (синусоидальные отмечают точкой).

Амплитуда инертной силы (в комплексном изображении) имеет вид:

пп

F_m = ю me ² Ve ' ⁰ = ю m Ve ² .

Точно также, имея в виду (3) и (4),

• •        k ' ' -•

F_k = —Ve ² = x ^ V .

ю к i- к - i- x =-Le 2 = ±e 2 =-'!..(10)

ю   юю

Это упругий реактанс в комплексной записи.

F_r = rV = rV .

r = r .

Это резистанс в комплексной записи.

В соответствии с этим амплитуды упругой и резистивной сил (в комплексном изображении) имеют вид:

• к - i ^П         к    - i ^П

F_k = -e ² Ve^l 0 = kVe ² . ю       ю

F_r = rV = re 0 ve 0 .

Комплексные представления механи-

ческих реактанса и импеданса:

x = x,

+ x =

„  - У ‘I m ю--I e 2 ю )

k У ‘П z = r + x = r + m ю -   e2

.

<     ю)

Абсолютная величина последнего совпадает с (8)

2 j.1          ^k

Z = r +1 тю--

.

У \ ю)

Фаза импеданса определяется формулой (5), поэтому

z = Ze' i ^ .

Сила внешнего источника имеет вид: F = zV = zve i ^ф .           (11)

Это подтверждается формулой (6).

Пример 1. F = 100 e i 0 (Н), ю = 2 рад/с , m = 10 кг , k = 20 ( кг • с “²),      r = 7( кг • с ^-1).

Определить все остальные параметры.

x_m =ю me 90 ° = 20 ei 90 ° ( кг • с ) ,

x = ^-e- i ⁹⁰ ° = 10 e ^-‘ 90 ° ( кг • с -¹). ю

^Z = ^ r 2 ⁺ ( x m - x k ) 2 =

= J7 2 + ( 20 - 10 ) 2 = 12,207 ( кг • с ) .

x_m - x       20 - 10

Ф = arctg —---k = arctg------= 55° , r7

z = Ze ‘ ⁹ = 12,207 e ‘ ⁵⁵ ° ( кг • с ) .

• •                         ⁰

V = - =    ^{00 e}     « 8,192 e-‘ 55° (м • с ^-1 ), (12)

z   12,207 e i ⁵⁵

• - m = x m V =

= 20 e i 90 ° • 8,192 e ^{-1 55} ° = 163,846 e i ³⁵ ° (Н),

• - k = x - V =

  = 10 e■¹90° • 8,192 e"^{1 55} ° = 81,923 e"^{1 145} ° (Н),

  -_r = rV = 7e i ⁰ • 8,192 e ^-‘ ⁵⁵ ° = 57,344 e ^-‘ ⁵⁵ ° (Н).

Как и следовало ожидать,

-_m + -_k + -_r= 163,846 e i ³⁵ ° + 81,923 e ^- ‘ ¹⁴⁵ ° +

+ 57,344 e ^- i ⁵⁵ ° = 100 e i ⁰ (Н) = - .

Расчет с применением дифференциальных уравнений занял бы несколько страниц.

Данным примера 1 соответствует векторная диаграмма на рис. 2.

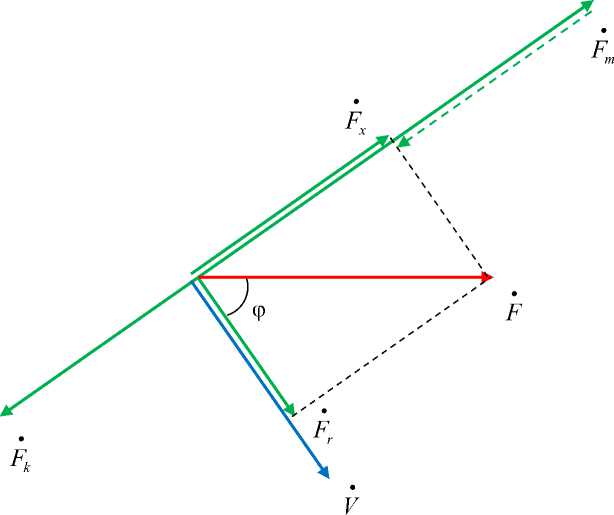
Рис. 2. Параллельное соединение

Пример 2. Для резонанса сил . Отличие от примера 1 состоит в том, что k = 40 ( кг ■ с ^{- 2}).

x = 20 e-i 90 ° ( кг ■ с -'), z = r = 7 eⁱ 0 ° ( кг ■ с ~'), •

V = F = 1^- - 14,286 e^{i 0} ° (M ■ с ^-1 ), z     7 e^{i 0}

F_m = x,V = 20 e i 90 ° ■ 14,286 e i 0 ° = 285,72 e i ⁹⁰ ° (Н), F k = XV =

= 20 e’ i ⁹⁰ ° ■ 14,286 e i 0 ° = 285,72 e"ⁱ 90 ° (Н),

F_r = rV = 7 e i ⁰ ■ 14,286 e i 0 ° = 100 e i 0 ° (Н).

Как и следовало ожидать,

F_m + F_k + F = 285,72 e i 90 ° + 285,72 e ^- i 90 ° + + 100 e i ⁰ ° = 100 e i ⁰ (Н) = F = F_r .

Данным примера 2 соответствует векторная диаграмма на рис. 3.

Схема последовательного соединения

Сила на элементах механической системы одинаковая (рис. 4):

f = F cos C) t .

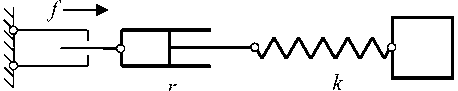
Рис. 4. Схема последовательного соединения

При этом скорости отличаются:

1F vm =    fdt =---sin ю t, mю vk

1 , dx 1 df ю

— k  =—— =sir k dt k dtk fF vr = — = — cos юt .

Рис. 3. Резонанс сил

Результирующая скорость:

v = v m ⁺ v k ⁺ v r =

= F

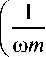
ю V  .1

— I sin ю t + -cos ю t k J        r

= F [1/ ( ю m ) - ю/ k ] 2 + (1/ r )² x

1( ю m ) - ю/ k

[ 1( ю m ) - ю/ k ] 2 + (1/ r )²

1 r

+ ,                            cos ю t .

VI [ 1^{( ю} m ) ^-ю/ ^k ]² + ⁽¹ r ^{) 2}       _

1 (ю m) - ю/ k ф = arctg n J---— .

1r v = F[1/(юm) - ю/k ]2 + (1/r)2 x x(sin ф sin ю t + cos ф cos ю t) =

= F [ 1/( ю m ) - ю/ k ] 2 + (1/ r )² cos( ю t - ф ) = = V cos( ю t - ф ) .

Это выражение синусоидальной скорости для схемы последовательного соединения элементов механической системы.

Амплитуда результирующе скорости:

V = Fy, y = V[V^m)-ю/k]2 + (Vr)2.      (16)

Из условия  1/(ю m) — ю/ k = 0 следует классическое выражение ю = ^k/m , получен- n

I ю 1   1 ■ у = g + b = g + 1 ----I e 2

-           ( k  ю m J ное значительно проще классического решения. При этом происходит резонанс скоростей [10]. При 1/r = 0, у = 0. Механизм препятствует (абсолютно) источнику колебаний.

Абсолютная величина последнего сов- падает с (16):

Y =

j^{g 2 + ( Ь}к ^{— b}m ) =

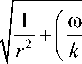
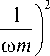
Комплексное описаниедля последовательной схемы соединения x bk — bm     x ю/k — -(юm)

Ф = arctg ----m = arctg —----—---- = gg

Алгоритм рассмотрения такой же, как и при параллельном соединении:

f = F cos ю t = Re( Fe i “ t ),

•         i n

F = Fe ² .

Из выражения (13) следует, что f опе- режает по фазе vm на п/2 .Таким образом,

•          1    • i П

V m =-- Fe ²

ю m

m ю m

п

- i —

••

= - F = b m F . x

— i-- = —.

ю m  x„

Это инертный сассептанс (susceptance) комплексной записи.

в

Амплитуда инертной скорости (в комплексном изображении) имеет вид:

•         1      — i ^П i ^П       1        „

V_m =--- e ² Fe ² =--- Fe ⁰ .

ю m       ю m

Точно также, имея в виду (14) и (15),

= arctg

r

(m ю — k/ ю) — mk у = Yeф .

Скорость штока внешнего источника имеет вид:

•         •          .       i ^П             i ( _Ф+^П )

V = yF = Yeⁱ ’ Fe ² = YFe ² .    (17)

Пример 3. Отличие от примера 1 состоит в том, что элементы соединены после- довательно.

b m = x m = 5 - 10 ^{— 2} e"^{i 90} ° ( кг -¹ • с ), b = x ⁴ = 10 - 10 ^{— 2} e^{i 90} ° (кг ^-1 • с), g = r-¹ = 14,286 - 10 ^{— 2} ( кг ^{— 1} • с ).

Y = Jg ² + ( b k — b m ) 2 =

= _A/(i428640 ^- 2 ) 27 ( i040 ^- 2^ 5^   =

= 15,135 - 10 ^{— 2} ( кг ^{— 1} • с ) .

• ro • i ^П 1    •          •

V =- Fe ² = — F = bF . kx

+ bk — b Ф = arctg —---- g

i b =-e 2 kk

. ю 1

= i— = — .

kx

x 10 •Ю—² — 5 •Ю—²  _1П^_О

= arctg------------ :— = 19,29 ° ,

14,286 •Ю — ²

Это упругий сассептанс в комплексной запи- у = Yeiф = 15,135 •Ю—2ei 19,29° (кг—1 • с).

си.

В соответствии с этим амплитуды упругой и резистивной скоростей (в комплексном изображении) имеют вид:

П

• •i- i-

• V =- e 2 Fe 2 =- FeП. kkk

• •      1 •          •

V_r = -F = gF = gFe ² .

r

1 g = g =- . r

Это кондактанс (conductance) в комплексной записи.

Комплексные представления механических сассептанса и адмитанса (admittance):

П

I ю 1    1 ⁱ 7

b = b + bn =1---I e ² ,

( k  ю m J

•         •

V = yF =

=15,135 • 10 ^{— 2} e^{i 19,29} ° • 100 = 15,135 e^{i 19,29} ° (м • с ^{— 1} ), V_m= bF = 5 • 10 ^{— 2} e~ⁱ 90 ° • 100 = 5 e~ⁱ 90 ° (м • с ^{— 1} ), V = bF = 10 • 10 ^{— 2} e^{i 90} ° • 100 = 10 e^{i 90} ° (м • с ^{— 1} ), V_r = gF = 14,286 • 10 ^{— 2} • 100 = 14,286 (м • с ^{— 1} ).

Как и следовало ожидать,

V_m + V_k + V_r = 5 e ^{— i 90} ° + 10 e^{i 90} ° + + 14,286=15,135 e^{i 19} , ²⁹ ° (м • с ^{— 1} ) = V .

Расчет с применением дифференциальных уравнений занял бы несколько страниц.

Данным примера 3 соответствует векторная диаграмма на рис. 5.

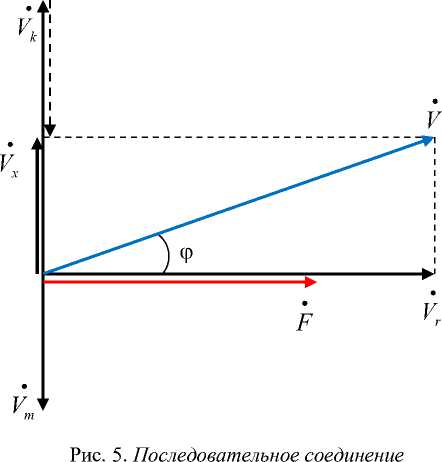
Связь между механическими величинами

Теорема 1. Имеет место выражение: 1

^{y —} I.

Доказательство . С учетом (11)

•

F

z —

—   •

V

С учетом (17)

.

•

V 1 y ^— “ ^—_

F ^z

Теорема доказана.

Следствие. При r — 0

.

Пример 4. Для резонанса скоростей . Отличие от примера 2 состоит в том, что элементы соединены последовательно.

b — 5 •Ю — ² e ⁹⁰ ° (кг ¹ • с),

Y = g = 14,286 •Ю—2 (кг-1 • с), ф — 0°, y — Yei’ = 14,286 • 10-2ei0° (кг-1 • с),

V — yF = 14,286 • 10 ^{— 2} • 100 = 14,286 ei ⁰ ° (м • с ^{- 1} ),

V — bF = 5 • 10 ^{— 2} e i ⁹⁰ ° • 100 = 5 e i ⁹⁰ ° (м • с ^{- 1} ).

Как и следовало ожидать,

V_m + V + V = 5 e - i ⁹⁰ ° + 5 e ⁹⁰ ° + 14,286=

=14,286 e‘ ⁰ ° (м • с ^{- 1} ) = V — V_r

Данным примера 4 соответствует векторная диаграмма на рис. 6.

• •.

V k

•

V

I► g►

••

FV

Так как при этом y — b , z — x .

Теорема 2. Для обратных эквивалентных величин имеют место выражения:

r g * — 222

n

x b * = 2----2 e 2, g r, g + b b— x * — —?----ee 2. “ g2 + b2

Доказательство .

У =

z

— — r + x — r + ix ,

1   r — ix _ r — ix r + ix r — ix r2 + x2

r

2 .    2

r ² + x ²

—

i ₂x ₂ — g * + b *, r + x

У = g + b — g + ib ,

• 1     1 g — ib g — ib

— —  —              —  2    2*

y g + ib g — ib g + b

g g2 + b2

—

i        , = r * + x *.

g ² + b²       “

Теорема доказана.

Теорема 3. Для схемы последовательного соединении механических систем имеет место выражение: n y—E y} • j—1

Доказательство . На все составляющие механические системы воздействует одна си-

ла F . Для любой из механических систем учетом (17) можно записать

с

•

•

V j = y j F .

В соответствии с принципом суперпозиции

•        n •         n        •       • n

•

V = E V j = E y j F = F E У = Fy .

Теорема 4. Для схемы параллельного соединении механических систем имеет место вы ражение: z = Ez, • j=1

Доказательство . Все составляющие механические системы имеют одну скорость •

V . Для любой из составляющих механических систем с учетом (11) можно записать

j = 1          j = 1

Теорема доказана.

j = 1

•

•

F, = ZV .

₁ n ₁

Следствие 1 — = E — z J = 1 Z j

В соответствии с принципом суперпозиции

•        n •         n       •      • n

•

^F = E F = E Z j V = V E Z j = Vz .

j = 1          j = 1

j = 1

n

П Zj

Следствие 2. _z = ^j = 1

nn

.

k = 1 j = 1 j * k

Следствие 3. Импеданс любой из

со-

ставляющих механических систем больше эквивалентного импеданса.

Теорема доказана.

₁ n ₁

Следствие 1. — = E—

У 'м y j

n

П yj

Следствие 2. _y = ^j = 1

nn

■ EП yj k=1 j=1 j * k

.

Следствие 4. Если

Z = Z =

...

= Z,- =

.

.

.

= Z n = Z *, то

z *

Z = — n

.

Следствие 3. Адмитанс любой из составляющих механических систем больше эквивалентного адмитанса.

Следствие 4. Если

Следствие 5.

У 1 = У 2 =

...

=yj =

...

lim z = zi^w

n

П Zj j=2

nn

.

Следствие

y *

= У п = У *, то У = ^ n

.

5. lim y = y j ^®“

n

П ^yj j— nn ЕП- y j k = 2 j = 2 j * k

.

ЕП zj k=2 j=2 j * k

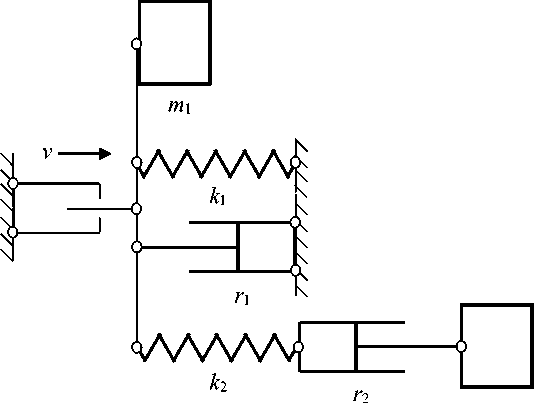
m 2

Рис. 7. Схема параллельно-последовательного соединения

Схема параллельнопоследовательного соединения (рис. 7)

С учетом теоремы 1

Z 2 = 1 y 2 .

С учетом теоремы 4 z = z + z . С учетом (11) V = F/z .

Пример 5. F = 100el0 (Н), ® = 2 рад/с, m = 10 кг, k = 20( кг • с-2), r = 7( кг • с-1).

Определить все остальные параметры.

Z = 1/ у = 1/(15,135 •ю^-2 ei ¹⁹ , ²⁹ ° ) « « 6,607 e-‘ ^19,29 ° (кг • с ^{- 1} ), Z = Z + Z = 12,207 e 55 ° + 6,607 e ’ ‘ ^19,29 ° = = 15,372 e 3057 ° (кг • с ^{- 1} ),

V = F/z = 100/(15,372 e ³⁰ ,5 ⁷ ° ) = = 6,505 e-' ^30,57 ° (м • с ^{- 1} ), F m 1 = x m 1 V = 20 e 90° • 6,505 e - ^30,57 ° = = 130,1 e ^59,43 ° (Н),

F = _&  V = 10 e- i ⁹⁰ ° • 6,505 e’ i³⁰⁵⁷ ° =

= 65,05 e-' ^120,57 ° (Н),

F_ri = rV ^ = 7 e i ⁰ • 6,505 e ^- ‘ ³⁰ 57 ° =

= 45,535 e ^- i ^30,57 ° (Н),

F r = ^V = 6,607 e- i ¹⁹ , ²⁹ ° • 6,505 e- i ³⁰ ,5 ⁷ ° =

= 42,979 e ^- i ^49,86 ° (Н),

V •г = b^Fi = 5 •Ю ^{- 2} e^i ⁹⁰ ° • 42,979 e- i ⁴ 9,8 ⁶ ° = = 2,149 e"^{i 139,86} ° (м • с ^{- 1} ),

V_k2 = b₂ F₂ = 10 • 10 ^{- 2} e ⁹⁰ ° • 42,979 e- i ⁴ 9,8 ⁶ ° = k 2      k 2   2

= 4,298 e^{i 40,14} ° (м • с ^{- 1} ),

V_r2 = g₂ F, = 14,286 • 10 ^{- 2} • 42,979 e ^- i ⁴ 9,8 ⁶ ° = = 6,14 e ^{- i 4} 9,8 ⁶ ° (м • с ^{- 1} ).

Расчет с применением дифференциальных уравнений занял бы несколько страниц.

Данным примера 5 соответствует векторная диаграмма на рис. 8.

Пример 6. Для параллельно-последовательного (двойного) резонанса. Отличие от примера 5 состоит в том, что k = 40 ( кг • с ~²).

z = Z = r = 7 e^{l 0} ° ( кг • с -*),

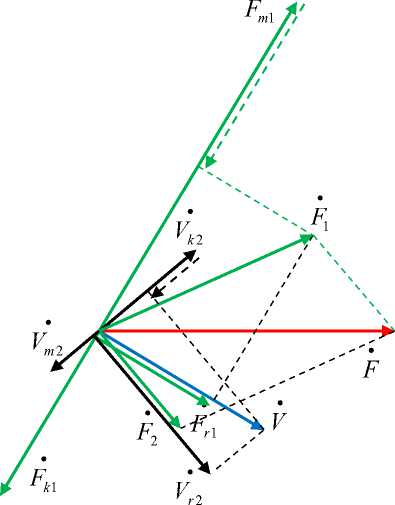
Рис. 8. Параллельно-последовательное соединение z = Z + Z = 2r = 14e0 (кг • с-1) ,

V = F/z = 100/(14 e 0 ° ) = 7,143 e 0 ° (м • с ^{- 1} ), •              •

F m 1 = x m 1 V = 20 e i ⁹^ 7,143 e i 0 ° =

= 142,857 e i ⁹⁰ ° (Н),

F _H= xj^ 20 e-i ⁹⁰ ° • 7,143 ei 0 ° =

= 142,857 e ^- i ⁹⁰ ° (Н),

F = F = rV = 7 e i ⁰ • 7,143 e i 0 ° = 50 e i 0 ° (Н),

F₂ = z₂V = 7e 0 ° • 7,143 e i 0 ° = 50 e i 0 ° (Н),

•               •

V m 2 = b m 2 F 2 = 5 •Ю ^{- 2} e - i ⁹⁰ ° ^ 50 e^{i 0} ° =

= 2,5e-‘90° (м • с-1), v’ = b2F2= 5 •ю-2 e 90° • 50 e 0° = k2     k2 2

= 2,5 e i ⁹⁰ ° (м • с ^{- 1} ),

V_r2 = g₂F₂ = 14,286 • 10 ^{- 2} • 50 e i 0 ° = = 7,143 e i ⁰ ° (м • с ^{- 1} ).

Данным примера 6 соответствует векторная диаграмма на рис. 9.

•

^Vk 2

•

F m1

•

F r 1 = F =F 2

•

^Vm 2

^=F

•       •

V r 2 = V

•

F

•

F k 1

Схема последовательнопараллельного соединения (рис. 10)

С учетом теоремы 1 y₂ = 1/ z .

С учетом теоремы 3 y = y + y ₂.

•         •

С учетом (17) скорость штока V = yF .

Пример 7. Отличие от примера 5 состоит в том, что элементы соединены последовательно-параллельно.

y₂ = 1/ z = 1/(12,207 e 55 ° ) =

= 8,192 - 10 -² e’ i 55 ° ( кг -¹ • с ),

У = y + y₂ = 15,135 - 10 — ² e ^19,29 ° + + 8,192 - 10 — ² e ’ i ⁵⁵ ° = 19,061 - 10 ^{- 2} e" i ^5,126 ° ( кг - • с ),

V = F y = 100 • 19,061 - 10 — ² e^^{i 5,126} ° = = 19,061 e- i ^5,126 ° ( м • с ^-1),

• V₂ = F y ₂ = 100 • 8,192 - 10 — ² e^^{i 55} = = 8,192 e’ i ⁵⁵ ° ( м • с -¹),

• - V + V ₂ = 15,135 e‘ ¹⁹ ,2 ⁹ ° + 8,192 e ^- i ⁵⁵ ° = =19,061 e - ⁱ 5,1 ²⁶ ° (м • с ^{- 1} ) = V .

Данным примера 7 соответствует векторная диаграмма на рис. 11.

Рис. 9 . Параллельно-последовательный (двойной) резонанс

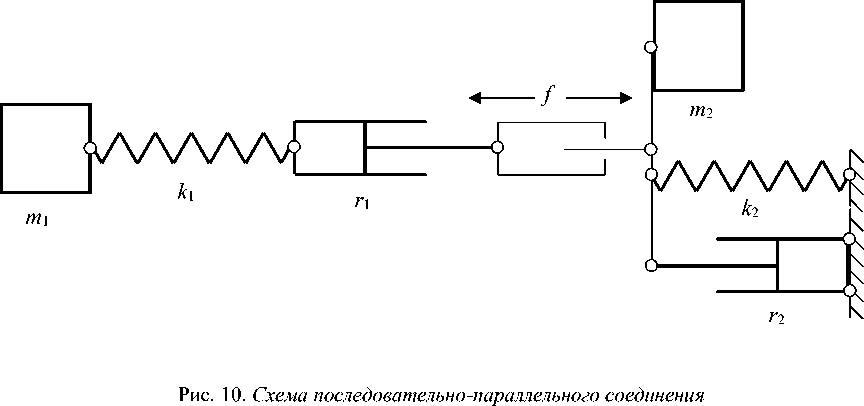
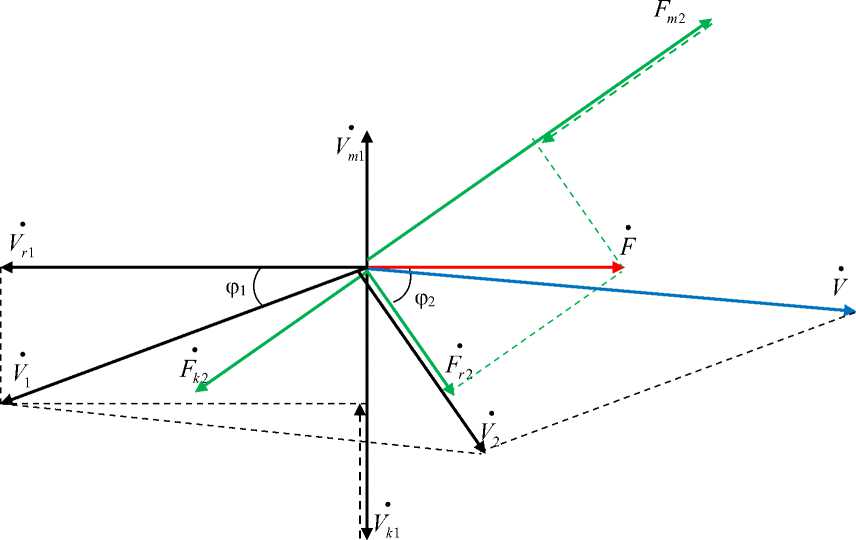
Рис. 11. Последовательно-параллельное соединение

Пример 8. Для последовательнопараллельного (двойного) резонанса отличие от примера 6 состоит в том, что элементы соединены последовательно-параллельно.

y 1 = V Z = g 1 = y 2 = V Z 2 = g 2 =

= V(12,207e'55) = 14,286 -10-2e'0° (кг-1 • с), y = У + y = 2 -14,286 -10—2e' 0° =

= 28,571 - 10 — 2 e ' ⁰ ° ( кг ^-1 - с ),

V = F y = 100 - 28,571 - 10 ^{- 2} e ' ⁰ ° =

= 28,571 e ' ⁰ ° ( м - с ),

• •         •      •

V = - V + V2,

• - V =- F У 1 = V 2 = F y 2 =

= 100 - 14,286 - 10 ^{- 2} e ' ⁰ ° = 14,286 e ' ⁰ ° ( м - с ),

•             •

• -    V m 1 = b m 1 F = 5 - 10 ^{- 2} e - ' ⁹⁰ ° - 100 e ' 0 ° =

= 5 e ^-190 ° (м - с ^{- 1} ),

• —    V L = ^F = 5 - 10 ^{- 2} e ' ⁹⁰ ° - 100 e ' ⁰ ° =

= 5 e ' ⁹⁰ ° (м - с ^{- 1} ),

• - V =- g_xF = 14,286 - 10 ^{- 2} - 100 e ' ⁰ ° =

= 14,286 e ' ⁰ ° (м - с ^{- 1} ),

F_ml = Х^₂ = 20 e' ⁹⁰ ° - 14,286 e' ⁰ ° =

= 285,714e'90° (Н), f’ = х,Л= 20e-'90° -14,286e'0° = k2

= 285,714e-'90° (Н), •        •       ••

F =F =F = r V = r 2       2           r22

= 7 e ' ⁰ - 14,286 e ' ⁰ ° = 100 e ' ⁰ ° (Н).

Данным примера 8 соответствует векторная диаграмма на рис. 12.

Характер реактивности импеданса

•

Если F = Fe‘ ⁰ ,

i arctg ^m

Z = r + X m = r^r + x m e r = ze ^ф,

то

•

V=- z

i 0

Fe— = —e -' ’ ze ' ’      z

Пример 9. При тех же количественных значений, что и выше,

x i arctg ^m

Z = rf + X m e r

= 4 7² + 20 2 e ⁷ « 21,19 e^{/ 70} ’ ⁷¹ ° ( кг - с ~‘),

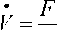
z

100 e^{i 0}

21,19 e ' ⁷ 0, ⁷¹ °

4,719 e ^- ' ⁷ 0, ⁷¹ °

( м - с ’) .

•

F m 2

•

V m 1

•       •

V = V VV 1

•      •

F = F r 2

V 2

V

•

^Vk 1

Данным примера 9 соответствует векторная диаграмма на рис. 13.

Пусть теперь iarctg k

Z = r + X k = r^{r 2} + x 2 e ^r = ze i ^Ф •

Рис. 13. "Инертный" импеданс

Пример 10. При тех же количественных значениях, что и выше, x iarctg k z = rr + Xk e   r =

- 10

= 77 27 10 2 e    ⁷ * 12,207 e -‘55 ° ( кг ■ с ~‘),

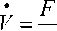
z

100 e^{i 0}

12,207 e ~‘ ⁵⁵‘

* 8,192 e ‘ ⁵⁵‘

( м ■ с ’).

Данным примера 10 соответствует векторная диаграмма на рис. 14.

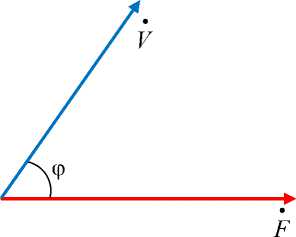
Рис. 14. "Упругий" импеданс

Из примеров 9 и 10 вытекает доказанная этими примерами

Теорема 5. Если сила опережает скорость по фазе, то нагрузка инертная, если отстает, то – упругая. Если фазы силы и скорости совпадают, то – резистивная (активная).

Замечание. При x = х + x и x <  x импеданс " упругий " . При х >  x импеданс " инертный " .

Теорема 6. Если х ^ x, то реактивный характер импеданса изменяется на противоположный при замене схемы соединения элементов (с последовательного на параллельное или наоборот).

Доказательство. Если х > x и соеди- нение параллельное, то x = xr

+ xk =

m ю —

k \ ‘ i

— I e a)

С учетом замечания к теореме 5 импеданс является " инертным " , при этом фаза ‘ п/2 >  0 .

Если эти же элементы соединить после- довательно, то

I ю

b = b + b = k         I k

—

1        ‘ п

— I e ² ю m )

a m — k /ю ‘ ^п e ²

km

С учетом следствия из теоремы 1

1        km      — ‘ П

=e 2 b  ю m — k /ю

Фаза поменяла знак (— i п/ 2 <  0 ).

Другими словами, импеданс стал " упругим " .

Очевидно, что при х <  x дело обстоит точно так же.

Теорема доказана.

Заключение

Использование символического (комплексного) описания механических систем -при вынужденных гармонических колебаниях (в установившемся режиме) позволило отказаться от чрезвычайно громоздкого и трудоемкого алгоритма расчета, связанного с решением дифференциальных уравнений и заменить его простыми и наглядными алгебраическими операциями. Благодаря этому время расчетов уменьшается в разы.

Для рассмотренных разветвленных механических схем классические методы, основанные на решении дифференциальных уравнений второго порядка, многократно усложняются и требуют решения систем уравнений, которые сводятся к дифференциальным уравнениям более высоких порядков.

Использование символического (комплексного) описания механических процессов и систем позволяет применять вместо этого простые и компактные алгебраические методы, трудоемкость которых меньше в десятки раз.

Векторные диаграммы, не являясь необходимой составляющей исследования механических систем, имеют существенное методическое значение, поскольку показывают количественные и фазные соотношения между параметрами систем.