Концентрационная конвекция в замкнутой области пористой среды при заданном вертикальном перепаде концентрации и учете иммобилизации примеси

Рассматривается концентрационная конвекция в замкнутой прямоугольной области пористой среды при заданном вертикальном перепаде концентрации и учете взаимодействия примеси с твердой матрицей среды. Транспортные процессы внутри пористых материалов активно изучаются в настоящее время при проведении как прикладных, так и фундаментальных исследований. Интерес к ним обусловлен широким спектром приложений, от изоляций зданий, химических каталитических реакторов до добычи полезных ископаемых.

Чаще всего процессы переноса в пористых средах описываются в публикациях в рамках классической модели «диффузия–адвекция» — Advection Diffusion Equation (ADE) [1] . В общем случае среда полагается обладающей сложной пространственной структурой, а примесь взаимодействует с твердой матрицей среды. Взаимодействие может иметь различные проявления: как химическая реакция [2] , прилипание бактерий к твердой стенке [3] , механическое затыкание порового канала частицами примеси или их агрегатами [4] , сорбция примеси на стенках поры [5] и другое. Поэтому при математическом моделировании массопереноса требуется учет множества дополнительных механизмов взаимовлияния [6] .

Ряд экспериментальных исследований [7 –9] показывает, что классическая модель (модель ADE) дает только общее представление о процессе, а характерные времена выноса примеси значительно отличаются от прогнозируемых [8] . Для более точного описания процесса предложена концепция мобильно-немобильной среды — MIM (калька с английского термина Mobile/Immobile Media) [10] . Этот подход учитывает взаимодействие частиц примеси с твердым скелетом пористой среды и основан на двухфазной кинетической модели диффузии. В рамках этого подхода предполагается, что примесь состоит из двух фаз: мобильной (свободной) и немобильной (связанной или адсорбированной). Мобильная примесь дрейфует с потоком или благодаря диффузионному механизму, и для нее записывается классическое уравнение диффузии со стоковым слагаемым, означающим приток примеси в немобильную фазу. Кинетика «фазового перехода» учитывается с помощью специфического кинетического уравнения, которое математически изображает процесс иммобилизации примеси. Вид уравнения зависит от механизма взаимодействия примеси со стенкой. В настоящей работе рассматривается наиболее распространенное взаимодействие — физическая сорбция, обусловленная поверхностными силами. При этом поток примеси между фазами является функцией концентраций примеси в обеих фазах. Простейшая модель

Статья опубликована в открытом доступе по лицензии CC BY 4.0

в рамках MIM-подхода — модель с кинетикой первого порядка, которая корректно описывает динамику переноса только при малых концентрациях примеси [11] . В такой модели интенсивность перехода примеси линейно связана с концентрациями обеих фаз. Существуют более сложные модели, см., например, [12] , которые учитывают насыщение немобильной фазы. Поскольку поверхность пор конечна, она не может адсорбировать сколь угодно большой объем примеси, для учета этого эффекта в кинетическое уравнение вводится нелинейность, ограничивающая интенсивность адсорбции при увеличении количества примеси в немобильной фазе. В таком случае процесс корректно моделируется уже в широком диапазоне концентраций примеси [13] .

Первые исследования неустойчивости, обусловленной плавучестью в насыщенных жидкостью пористых массивах, представлены в работе [14] . Авторы рассматривали пористый слой, бесконечный в горизонтальном направлении, но ограниченный по вертикали двумя непроницаемыми границами, между которыми задавался постоянный перепад температуры. Таким образом, поперек слоя обеспечивался постоянный равновесный градиент температуры. Получены уравнения, описывающие конвективное течение в слое. Оценены пороговые условия для возникновения неустойчивости. Показано, что конвекция образуется монотонным образом при достижении числом Релея-Дарси значения 4п 2 .

Эта же задача в работе [15] решена в присутствии постоянного горизонтального потока жидкости вдоль слоя. Обнаружено, что порог зарождения неустойчивости не зависит от скорости внешнего потока. Однако конвекция возбуждается колебательным образом, а частота колебаний пропорциональна скорости потока. В работе [16] в эксперименте по прокачке жидкости через длинную (с соотношением высоты к длине 1/3) область пористой среды, подогреваемой снизу, показана справедливость результатов в [15] . Установлено, что при значениях числа Пекле, больших 0.75, и числах Релея–Дарси, меньших 240, наблюдается колебательная конвекция, причем ее интенсивность не влияет на расход жидкости в горизонтальном направлении. Работа [17] посвящена изучению тепловой конвекции в замкнутой области пористой среды при малых скоростях внешнего потока. Выяснено, что для достаточно коротких (с соотношением высоты к длине больше 1) областей пористой среды конвекция возникает монотонным образом, а безразмерная интенсивность теплопереноса пропорциональна квадрату числа Пекле. В [18] этот эффект подтвержден в рамках модели фильтрации Форгеймера. Таким образом, очевидно, что должен существовать некоторый переход от монотонного конвективного течения к колебательному при увеличении как горизонтальных размеров области, так и числа Пекле.

Отдельный интерес представляет исследование связи взаимодействия примеси с пористой средой и колебательного режима конвекции. Как показано в работах [19 –21] , такое взаимодействие в рамках MIM-подхода может сказываться только на нестационарных конвективных течениях, и обычно иммобилизация приводит к стабилизации основного течения. В стационарном случае кинетическое уравнение дает равновесное распределение примеси между мобильной и немобильной фазами. При этом потоки примеси между ними прекращаются.

Таким образом, цель настоящей работы заключается в исследовании перехода от монотонного к колебательному режиму конвекции и изучении влияния на этот переход иммобилизации примеси.

• 2.    Модель транспорта примеси в пористой среде с учетом иммобилизации

Транспорт через пористую среду часто осложнен взаимодействием примеси с твердой матрицей пористой среды. При его описании с учетом иммобилизации наиболее популярен подход MIM [10]. Концепция MIM имеет в основе разделение всей примеси на две фазы: мобильную (подвижную, свободную) и немобильную (иммобильную, связанную, адсорбированную). Для последовательного построения модели транспорта примеси в рамках MIM-подхода рассмотрим некоторый объем пористой среды V . В случае, когда примесь в среде отсутствует (будем называть такую среду чистой), ее поровый объем равен V0 и тогда ф0 = V0/V — пористость чистой среды. При полном заполнении пор смесью, включающей в себя примесь и несущую жидкость (насыщенная пористая среда), очевидно, будет выполняться соотношение: V0 = Vl + Vm + Vi, где V — объем несущей жидкости, а Vm , Vi — объемы мобильной и немобильной фаз примеси. Поскольку немобильная примесь занимает лишь некоторый объем поры и не может в нем непосредственно перемещаться, то она сокращает доступный для заполнения подвижной частью смеси поровый объем: Vp = V + Vm. Положим величину ф = Vp/V — текущую пористость среды с учетом сократившегося объема пор, как фо = ф+Vi/V = ф+Q, (1)

где Q = Vi/V — объемная концентрация немобильной примеси или немобильная концентрация (такое определение весьма необычно, но сложилось исторически и удобно с практической точки зрения). Напротив, концентрация мобильной примеси или мобильная концентрация находится стандартным образом: C = Vm/Vp, то есть по отношению к объему подвижной части смеси. Уравнение сохранения массы несжимаемой примеси в терминах C и Q может быть записано как f Pa dt (Q + ^C)dV = -f

P a div( u C -фDVC )dV,

VV где t — время, pa = const — плотность примеси, u — вектор скорости фильтрации, D — эффективный коэффициент диффузии, ∇ — дифференциальный оператор Гамильтона. При транспорте в пористой среде коэффициент диффузии зависит не только от состава смеси, но еще и от структуры самой среды [22, 23]. В предположении несжимаемости примеси представим уравнение в дифференциальной форме:

д

— (Q+фС ) = -div( u C -фDVC ).

При дополнительном условии несжимаемости несущей жидкости (p l = const) условие несжимаемости смеси в стандартной форме выражается как div u = 0 (см. [24] ). Тогда, с учетом (1) и в предположении D = const, уравнения транспорта несжимаемой смеси принимают вид:

д

— (Q+фС ) = - u -VC+DфЛC+ DVф •VC, ∂t

ф = фо-Q, divu = 0, где Л — дифференциальный оператор Лапласа. Система (4) должна быть дополнена уравнением, описывающим переход примеси между фазами, то есть кинетическим уравнением, а также законом фильтрации.

Будем рассматривать взаимодействие примеси с матрицей по наиболее распространенному механизму физической сорбции [5] . Согласно работам [12, 13] , в достаточно широком диапазоне концентраций кинетика сорбционного процесса может быть представлена следующим уравнением:

dQ = a(C (q o -Q) -K d C ),

где α — коэффициент переноса примеси, K _d — коэффициент распределений примеси, q ₀ — концентрация насыщения примесью твердой матрицы среды. Уравнение (5) достаточно универсально, оно отвечает большинству сорбционных процессов, сопровождающихся насыщением адсорбированной фазы [12] . Подобное уравнение впервые использовал Ленгмюр при исследовании адсорбции газов [25] . В качестве закона фильтрации воспользуемся хорошо зарекомендовавшей себя моделью Дарси–Буссинеска [26] :

u = - ^K VP+р 1 в с C g ,

где κ — проницаемость среды (в общем случае является функцией пористости), η — кинематическая вязкость, ρ _l — плотность несущей жидкости, P — отклонение давления от гидростатического распределения, β c — коэффициент концентрационного расширения, g — вектор ускорения свободного падения.

Рассмотрим среду с малыми концентрациями примеси, то есть ϕ 0 C ∼ Q ≪ q 0 ∼ ϕ 0 . Тогда, согласно [11, 21] , можно считать, что ф = ф ₀ - Q « ф ₀ = const, к = const, у = const, и система определяющих уравнений (4) - (6) становится следующей:

(Q +C ) = - Т•VC+DЛC,

∂t ϕ 0           ϕ 0

д^ = ^{a ( q} 0 ^C-K d ^{C ),}                                   (7)

u = - к VP+Р1вс Cg, η divu = 0.

• 3.    Постановка задачи

  

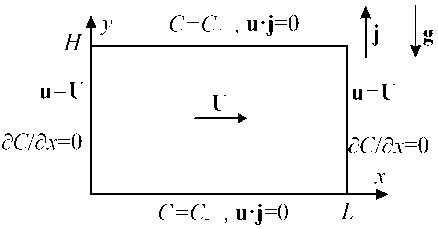
  Рис. 1. Схема задачи

  
  

Решим задачу возникновения концентрационной конвекции в пористой среде, находящейся в замкнутой прямоугольной области размерами L х H, с учетом взаимодействия примеси с твердой матрицей среды при заданном вертикальном перепаде концентрации. Схематичное изображение расчетной области представлено на рисунке 1. В поле силы тяжести при наличии вертикального перепада концентрации тяжелой примеси создается неустойчивая стратификация примеси, что приводит к возникновению конвективного течения, а это означает, что C+ >C-.

Присутствие горизонтальной прокачки через рассматриваемый пористый массив, согласно [16, 19] , может привести к колебаниям. Известно [17] , что в узкой рабочей области при слабой прокачке конвекция возникает монотонным образом, а в длинной области в присутствии интенсивного внешнего фильтрационного потока наблюдается колебательная мода неустойчивости [16] . Более того, хорошо известно, что в бесконечном слое [15, 19] при любой сколь угодно слабой прокачке конвекция возбуждается только колебательным образом. Исследуем условия перехода от монотонного к колебательному режиму конвекции.

Задача, схему которой содержит рисунок 1, математически, в рамках модели (7) , записывается следующим образом:

∂Q dt фo

- -U- •VC+ D^C, ^ф 0

dQ — a(q o C - K d C ), div u — 0, u —-n v p - p i в с Cg j , u —(u,w), C | y = H — C + , C | y =o — C - , w| y =o ,H — 0,

∂C ∂x

— °, u|x=0,L — U, wlx=0,L — 0, где j — единичный вектор, направленный вдоль вертикальной оси навстречу вектору силы тяжести, U — скорость внешнего фильтрационного потока. Обезразмерим уравнения (8), для этого воспользуемся следующими масштабами для расстояния, времени, фильтрационной скорости, давления, мобильной и немобильной концентраций, соответственно:

[L]— H, [t] — H ² , [u,w] — D, [P] — ^{Ф 0 ипН}, [C ]— C ₊ - C - — C o , [Q] — ф о C o .         (9)

DHκ

С учетом масштабов (9) задача (8) в безразмерном виде представляется как d ,                      _

• - (Q+C) — - u -VC+ AC,

∂t

^Q — aC - bQ, divu — 0, ∂t u — -PeVP - RpCj, u —(u,w),                             (10)

C l y =1 — 1 C l y =o —^0, w| y =o , 1 —^0,

∂C ∂x

• ^{— 0, u |} x =o ,l ^{—Pe, w |} x =o ,l ^—0 x =o ,l

и содержит пять безразмерных параметров: Rp — Kp l в_сgHC _o /(ф ₀ gD) — число Релея-Дарси, характеризующее действие сил плавучести; Pe — UH/D — число Пекле, определяющее интенсивность внешней фильтрации; a — aH ² q _o /(Dф ₀ ), b — aK d H ² /D— безразмерные параметры адсорбции и десорбции; l — L/H— геометрический параметр.

Задача (10) имеет одномерное решение, соответствующее основному состоянию, полученному в работах [15, 19] ; это решение описывает режим стационарной горизонтальной фильтрации и имеет вид (нижним индексом «1»

отмечены величины, относящиеся к этому решению):

C = C i (y)= y, Q = Q i (y) = by, u = U 1 = (Pe,0), P = P i (x,y) = -x- Rp y~.          (11)

При двумерных возмущениях решение (11) может быть неустойчивым по отношению к малым возмущениям, поскольку оно моделирует неустойчивую стратификацию плотности: более тяжелая жидкость находится над легкой. Вследствие такой неустойчивости и возникает конвективное течение.

Рассмотрим малые возмущения режима горизонтальной фильтрации:

C-^C i = A^ 1, ^Q—Q i = q ^ 1, ^p-P i = p ^ 1, ^u - u i = f ,- \ l u - u i |^P^e,      ⁽¹²⁾

∂y ∂x где ψ — функция тока для возмущений скорости. Оставляя в (10) лишь линейные по возмущениям слагаемые и исключая возмущения давления, с учетом (12) получим линейную задачу устойчивости:

∂ 2 ψ ∂ 2 ψ     ∂c ∂q дХ 2 + дУ 2 =RpдX, at = ac-Ьq, ∂c ∂q      ∂c ∂ψ ∂ 2 c ∂ 2 c д^ дt      дх^дх^дх 2^ ду 2 ■                           (13) c | y = 0 , i =0, X| y = o , i =0, дс XX-        =0, $| x =0 ,l =0 . ∂x x =0 ,l

• 4.    Методика решения задачи устойчивости

Решение задачи (13) будем искать в нормальной форме:

A = A(x)sin(ny)exp(At), q = q(x)sin(ny)exp(At),                                         (14)

$ = $ (x)sin(ny)exp(At).

Здесь А = y+iw, где y и w — инкремент и частота возмущений. Подставляя решение в форме (14) в систему (13), получим:

∂ ² ψ ∂x ²

-п²^ = Rp —,

ac

" а ■

А2 + А(а+b) _      дс ди д2c а+b   c=-Pe дХ + dx+дХ2

∂c ∂x

= 0,   Xl x =0 ,i = 0.

x =0 ,l

Для поиска полей концентрации и функции тока (A, ψ) воспользуемся методом Галёркина [27], то есть представим их распределения в виде соответствующих рядов:

N

A = ^C n COs

N

$ = ^J^n sin

Подставим (16) в (15) :

N2

п2 X$n f 22 +1 sin () = nRpX J Cnsin n=1

А ² +А(а+b) N-y /nnx\

А+  XCnCOs(

N

n

= nPe 2^ — Cn sin

N

N

Очевидно, что первое из уравнений (17) эквивалентно соотношению:

Rp nl

^n = ПГ7+Р ^c

После подстановки (18) во второе уравнение системы (17) находим:

N

X n=1

A ² +A(a+b) A+b

+n ²

n ²

p ⁺¹

Rpn ² n ² +1 ²

N cncos( nnx ) = nPeX ncnsn

Согласно процедуре метода Галёркина [27] , домножим (19) на cos(nkx/l), проинтегрируем по координате x на отрезке [0,1], то есть по длине рассматриваемой обрасти. В результате получим:

N

BkAk - ^Ak,ncn = 0, k = 1,...,N, n=1

B

l k =2

A ² +A(a+b) A+b

+n ²

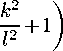
Rpk ² k ² + l ²

0 , k = n,

Pe [ (-1) ^k+n -1 j n ² / ( k ² -n ² ), k = n.

Для существования нетривиального решения системы линейных уравнений (20) должно выполняться следующее условие:

| W | =

B 1

A ₂₁

A 12

B 2

A in  A 2 N

A 1 N

A _{2 N}

.

.

.

B N

= 0.

Комплексное уравнение (21) позволяет найти зависимость частоты и инкремента от параметров задачи. Оценим нейтральные возмущения, то есть те, для которых y = 0. Они соответствуют моменту бифуркации — переходу от устойчивого режима горизонтальной фильтрации к конвективному двумерному течению. Согласующиеся с ними значения числа Релея-Дарси будем называть критическими (Rp c ).

Уравнение (21) решалось численно, методом двумерных секущих [28] . Получены нейтральные кривые: зависимости критического значения числа Релея–Дарси и частоты нейтральных возмущений от параметров задачи. Размерность матрицы W определяется числом N — числом использованных в разложении (16) функций. Во всех расчетах, результаты которых представлены ниже, число функций составляло: N = 40. Такой выбор обусловлен сходимостью процедуры численного решения, которая обсуждается в следующем разделе.

• 5.    Результаты

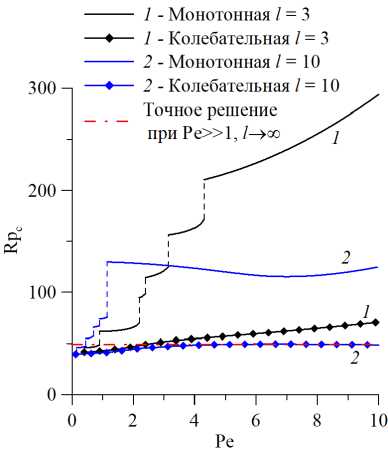
Исследование условий перехода от монотонной моды возбуждения конвекции (когда ш = 0) к колебательной (при ш = 0) является основной мотивацией выполнения данной работы. Известно [17] , что в областях ограниченной длины при малых скоростях фильтрационного потока наблюдается монотонная мода, в длинных и при значительной интенсивности прокачки [16, 19] возникают колебания. Изучение перехода начнем с анализа нейтральных кривых, приведенных на рисунках 2 -4 в плоскости параметров Pe и Rp c . На рисунке 2а показан характерный вид нейтральных кривых в плоскости параметров (Pe,Rp c ) для монотонной и колебательной мод неустойчивости. Уравнение (21) в случае ш = 0 (монотонная мода) представляет собой полином степени N относительно параметра Rp A . Известно, что такое уравнение имеет N решений на множестве комплексных чисел. Нейтральная кривая содержит зависимость только наименьшего действительного значения Rp a от числа Pe. При его изменении некоторое решение уравнения (21) может становиться комплексным, и тогда нейтральная кривая терпит разрыв, а наиболее опасным становится решение этого уравнения с другим корнем. Разные решения соответствуют различной структуре течения, например, для l = 3 при малых Pe течение содержит три конвективных вала; после первого разрыва, при Pe и 0.41, монотонная мода сменяется течением, содержащим только два вала. Однако, как показало исследование, для рассматриваемой задачи при первом же разрыве монотонной моды

( a )

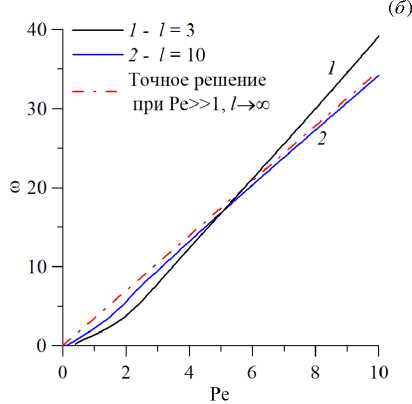
Рис. 2. Нейтральные кривые в плоскости (Pe,Rp c ) ( а ) и зависимости частоты нейтральных возмущений от числа Пекле Pe ( б ) при безразмерных параметрах сорбции a = 5 , b =5 и двух значениях параметра l , характеризующего длину расчетной области; кривые построены для монотонной (сплошные линии, штриховые участки которых отвечают скачкам) и колебательной (символы) мод неустойчивости; штрихпунктирной линией показано аналитическое решение [19] для больших значений числа Пекле и бесконечного слоя

появляется решение, отвечающее колебательной моде (ш = 0), и последнее решение остается наиболее опасным при дальнейшем увеличении параметра Pe.

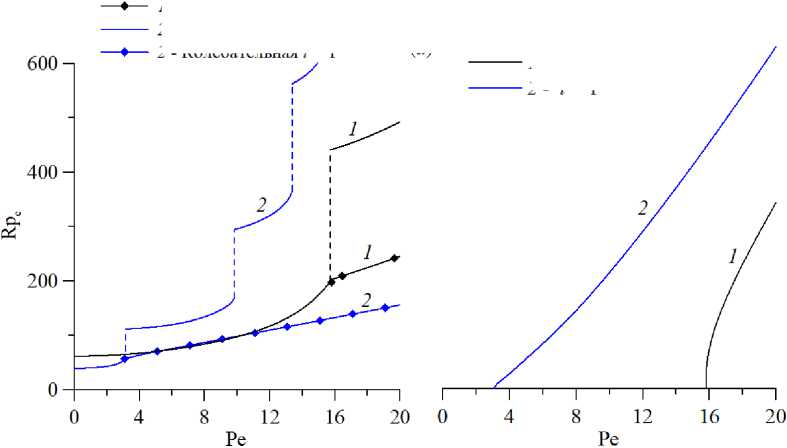
В решаемой задаче наибольший интерес представляет исследование зависимости Rp c и ш от двух параметров: Pe и l, так как, согласно [19] , изменение параметров сорбции не оказывает никакого влияния на монотонную моду. Для представленных на рисунке 2 значений длины рабочей области монотонная мода реализуется только при очень малых числах Пекле: так, для l = 3 это Pe < 0.41, a для l = 10 она наблюдается при Pe < 0.12. Хотя решение, согласующееся с отсутствием колебаний, есть всегда, но в широком диапазоне чисел Пекле оно соответствует большим, чем колебательная мода, значениям числа Релея-Дарси. К тому же при l = 10 и Pe > 6 нейтральная кривая и частотная зависимость близки к аналитическому решению, полученному в [19] для бесконечного слоя. В случае короткой рабочей области (l <  1) для возбуждения колебаний требуются большие числа Релея-Дарси и Пекле, что подтверждает рисунок 3. Здесь представлены нейтральные кривые и зависимости частоты нейтральных возмущений от числа Пекле для расчетной области малой длины (l = 1 и l = 0.5). В первом случае (l = 1) колебания наблюдаются при Pe > 3.15, при этом критическое значение числа Релея-Дарси существенно выше, чем для протяженных областей, и продолжает увеличиваться при росте числа Пекле. В области длиной l = 0.5 для обнаружения колебаний требуются еще большие числа Пекле (Pe > 15.7), и, что важно, в целом значительно возрастает порог возникновения конвекции по Rp _c . Частота колебаний для более короткой области тоже выше. Хотя последний тезис справедлив только для достаточно коротких рабочих областей. Так, для двух протяженных рабочих областей частоты близки друг к другу; частота для той из них, которая короче, может быть выше (см. Рис. 2) .

Результат более подробного исследования зависимости критических значений параметров от длины области представлен на рисунке 4. Приведены нейтральные кривые (Рис. 4а ) и зависимости частоты нейтральных возмущений от геометрического параметра l. Так же, как и ранее, показаны монотонная и колебательная моды неустойчивости. Кривая, описывающая монотонный режим, содержит разрывы, как и соответствующая зависимость от числа Пекле. При некоторой длине области возникает колебательная мода, которая становится наиболее опасной. При дальнейшем увеличении длины области критическое значение числа Релея–Дарси, отвечающее колебательной моде, убывает, стремясь к решению для бесконечного горизонтального слоя [19] . При этом Rp _c всегда остается меньше значения, согласующегося с монотонной модой, потому приводить монотонное решение во всем рассматриваемом интервале l не имеет особого смысла, поскольку рисунок будет перегружен дополнительными деталями. Вместе с тем установлено, что при увеличении числа Пекле значение параметра l, необходимое для обнаружения колебаний, имеет меньшую величину, так для Pe = 1 колебания

( a )

1- / = 0.5

2- M

1 - Монотонная I = 0.5

1 - Колебательная / = 0.5

2 - Монотонная / = 1

2 - Колебательная I = 1

( б )

Рис. 3. Нейтральные кривые на плоскости (Pe,Rp c ) ( а ) и зависимости частоты нейтральных возмущений от числа Пекле Pe ( б ) при безразмерных параметрах сорбции a = 5 , b = 5 и двух значениях параметра l , характеризующего длину расчетной области; кривые построены для монотонной (сплошные линии, пунктирные штриховые участки которых отвечают скачкам) и колебательной (символы) мод неустойчивости

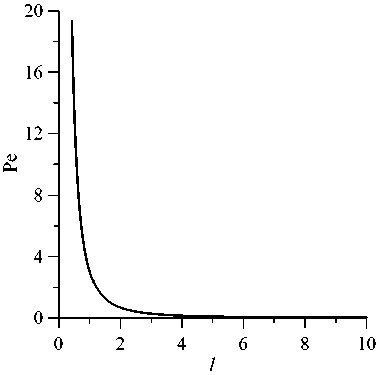
наблюдаются при l > 1.89, а для Pe = 5 при l > 0.86. Характерные частоты колебаний повышаются с ростом числа Пекле (см. Рис. 4б ). Для обобщения данных о возникновении колебаний построены карты существования колебательной неустойчивости (Рис. 5) . Соответствующие конкретному значению частоты ω = 10 ^-5 , они тем не менее подтверждают выводы, сделанные выше: критические значения параметров резко увеличиваются при уменьшении длины области. Так, на рисунке 5 карты существования начинаются со значения l = 0.4, что дает Pe = 19.4 и Rp _c = 342.5. При увеличении l эти значения практически по экспоненциальному закону устремляются к классическому решению Pe=0, Rp _c = 4π ² , найденному в [15] для бесконечного слоя пористой среды. Карты существования не зависят от значений параметров сорбции (потому этот факт не указан в подписи к Рис. 5) . В работе [19] показано, что наличие иммобилизации (изменение параметров сорбции) никак не влияет

( a )

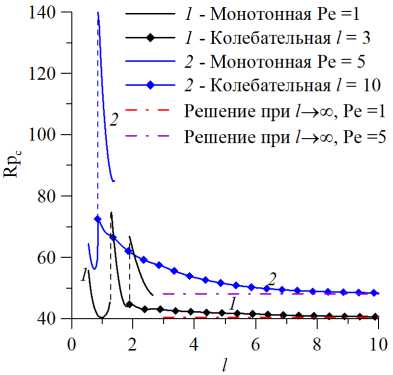
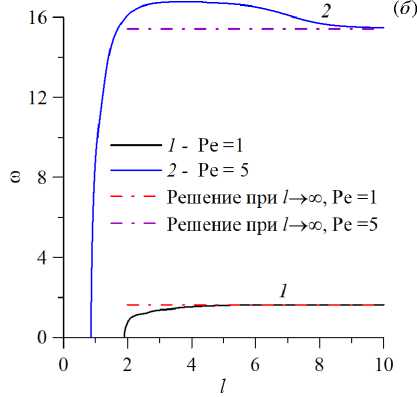
Рис. 4. Нейтральные кривые на плоскости (l,Rp c ) ( а ) и зависимости частоты нейтральных возмущений от геометрического параметра l ( б ) при безразмерных параметрах сорбции a = 5 , b = 5 и двух значениях числа Пекле; кривые построены для монотонной (сплошные линии, штриховые участки которых отвечают скачкам) и колебательной (символы) мод неустойчивости; штрихпунктирными линиями показаны решения, полученные в [19] для бесконечного горизонтального слоя

на монотонную моду, но повышает устойчивость горизонтальной фильтрации по отношению к колебательному режиму.

( a )

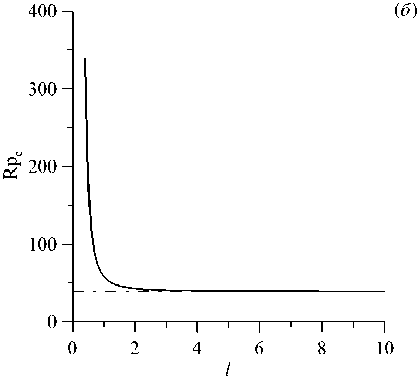
Рис. 5. Карта существования колебательной неустойчивости на плоскостях параметров (l,Pe) ( а ) и (l,Rp c ) ( б ); штрихпунктирной линией показано классическое решение при Pe = 0 , Rp = 4n 2 , полученное в [15] для бесконечного горизонтального слоя

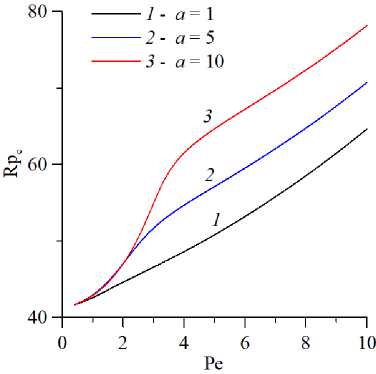
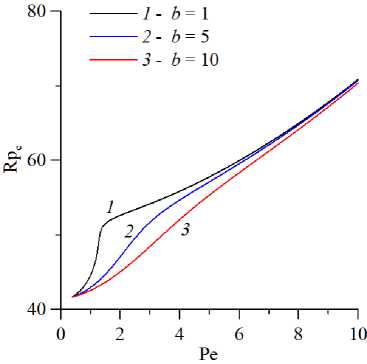
По данным исследования влияния иммобилизации на конвекцию построены нейтральные кривые для колебательной моды при разных значениях параметров сорбции (Рис. 6 –8) . На рисунке 6 представлены нейтральные кривые (Рис. 6а ) и зависимости частоты нейтральных возмущений от числа Пекле (Рис. 6б ) при нескольких значениях параметра адсорбции a. Видно, что увеличение интенсивности иммобилизации (повышение a) приводит к стабилизации, поскольку примесь активнее изымается из мобильной фазы, и тем самым ослабляется неустойчивая стратификация. При этом для сравнительно малых значений числа Пекле динамика колебательного процесса замедляется с ростом адсорбции. С увеличением числа Пекле частоты становятся близкими, а зависимость приближается к линейной. Влияние параметра десорбции b показано на рисунке 7. Рисунок содержит нейтральные кривые (Рис. 7а ) и зависимости частоты нейтральных возмущений от числа Пекле (Рис. 7б ) при нескольких значениях параметра десорбции. Видно, что изменение b приводит к эффектам, противоположным к тем, которые вызывает изменение a, а именно, приводит к дестабилизации и интенсификации колебательной динамики. Влияние вариации параметра адсорбции а на нейтральные кривые на плоскости (l,Rp _c )

( a )

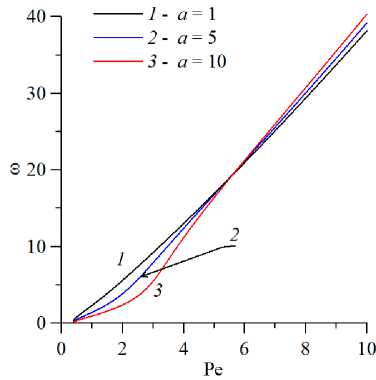
Рис. 6. Нейтральные кривые на плоскости (Pe,Rp c ) ( а ) и зависимости частоты нейтральных возмущений от числа Пекле Pe ( б ) для разных значений параметра адсорбции а; кривые построены для колебательной моды неустойчивости при l = 3 , b = 5

можно оценить по рисунку 8.

( a )

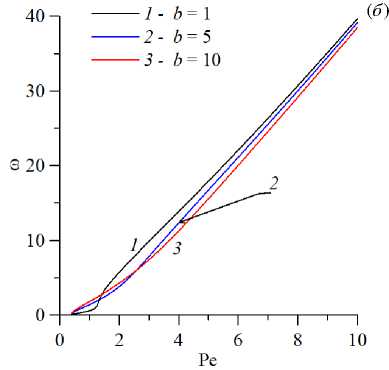
Рис. 7. Нейтральные кривые на плоскости (Pe,Rp c ) ( а ) и зависимости частоты нейтральных возмущений от числа Пекле Pe ( б ) для разных значений параметра десорбции b ; кривые построены для колебательной моды неустойчивости при l = 3 , a = 5

( a )

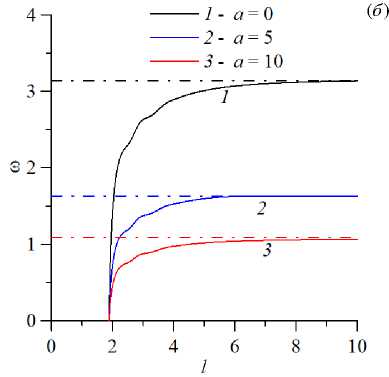
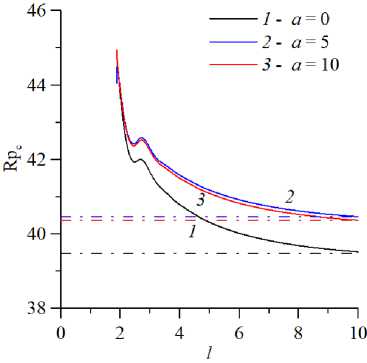
Рис. 8. Нейтральные кривые на плоскости (l,Rp c ) ( а ) и зависимости частоты нейтральных возмущений от геометрического параметра ( l ) ( б ) для разных значений параметра адсорбции a ; кривые построены для колебательной моды неустойчивости при Pe = 1 , b = 5

Из рисунков 5 –8 следует, что факт возникновения колебаний никак не зависит от интенсивности сорбционных процессов: значения критических параметров вблизи порога зарождения неустойчивости близки. С ростом протяженности расчетной области значения расходятся. На рисунке 8 представлен предельный случай — отсутствие иммобилизации (см. кривые 1 ), свидетельствующий, что для длинной области характеристики стремятся к значениям, отвечающим классическому решению (Rp = 4π ² , ω = πPe). На рисунке 8а видна немонотонная зависимость критического значения числа Релея–Дарси от параметра адсорбции. Эта особенность замечена в работе [19] и связывается с ограничениями, присущими линейной модели иммобилизации: поскольку объем адсорбируемой примеси неограничен, то происходит перенасыщение немобильной фазы; процесс десорбции практически останавливается, а критическое значение числа Релея–Дарси при a → ∞ устремляется к Rp = 4π ² (это же значение достигается при a = 0). Вместе с тем частота монотонно увеличивается с ростом как адсорбции a, так и протяженности области и приближается к значениям, соответствующим случаю бесконечного слоя.

При анализе результатов вычислений целью ставилось выявление физических эффектов и механизмов возникновения конвекции. Однако необходима также проверка сходимости разработанного метода в зависимости от N — числа используемых членов в рядах (16). Итоги этого исследования представлены в следующем разделе статьи. Здесь стоит упомянуть, что все расчеты произведены при N = 40.

• 6.    Анализ сходимости метода

Известно [29] , что быстрая сходимость метода Галёркина достигается только для самосопряженных задач. Задачи с наличием внешних течений таким свойством не обладают, а в рассматриваемой задаче исследуется устойчивость однородного течения. Собственно, и сама необходимость применять приближенный численный метод возникает из-за присутствия в разрешающей системе единственного слагаемого, пропорционального числу Пекле, то есть вследствие учета внешнего течения. В связи с этим необходим анализ сходимости метода и оценка числа членов ряда, требующегося для корректного решения задачи с выбранными параметрами. Прежде всего, это число Пекле и длина рабочей области: Pe € [0,20], l € [0.2,10]. Так, очевидно, что для l >  N разложение в ряд не может описать структуру течения, наблюдающегося в бесконечном слое. Его структура — это множество конвективных ячеек, длина которых в два раза больше высоты слоя, которая представляется функциями вида [15, 19] : ф ^ sin(nx), c ~ cos(nx). Более того, при недостаточном количестве функций в разложении могут наблюдаться эффекты, которых не должно быть, обоснование которых не существует. Например, рассмотрим нейтральные кривые на плоскости (Pe,Rp _c ) при l = 1 и N = 3 (Рис. 9) .

( a )

---- 1 - Монотонная N =3

—♦— 1 - Колебательная N =3

---- 2 - Монотонная ^= 40

—•— 2 - Колебательная N = 40

( б )

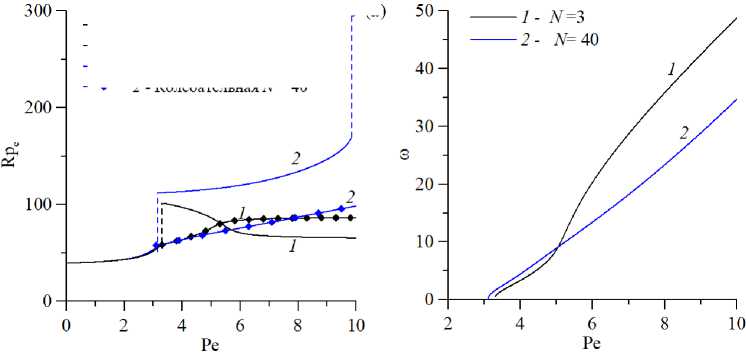
Рис. 9. Нейтральные кривые на плоскости (Pe,Rp _c ) ( а ) и зависимости частоты нейтральных возмущений от числа Пекле Pe ( б ); кривые построены для монотонной и колебательной мод неустойчивости при N = 3 (плохая точность) и N = 40 (удовлетворительная точность) для l = 1 , a = 5 , b = 5

Рисунок 9 демонстрирует, что при N = 3 наблюдается сильное уменьшение критического значения числа Релея–Дарси после разрыва монотонной моды, что приводит к смене режима с колебательного снова на монотонный. Этот результат является следствием плохой точности решения. Решение, полученное с достаточной точностью (N = 40), практически совпадает с N = 3 только на начальном участке (Pe < 3), где наиболее опасна монотонная мода. Физической причины обратной смены режима с монотонного на колебательный нет, поскольку сама природа колебаний, заключающаяся в сносе образующихся конвективных ячеек внешним потоком, при увеличении потока должна только интенсифицироваться.

Другая проблема — исчезновение решения, соответствующего монотонной моде, при четном числе функций в разложении. Для малых значений N это может происходить до появления колебательной моды, поскольку формально уравнение способно иметь корни, отвечающие комплексной частоте. Рассмотрим простейший случай монотонной моды ш = 0 при N = 2. Тогда определитель (21) запишется как

| W | =

B 1

A 21

A 12

B 2

n ² l ( 1+l ² \    Rp

2 \ l ² J 1 + l ² Pe

- ”3"

4Pe n2l / 4+l2 \ Rp4

l ² J 4+l ²

или

Rp ²        ₂      5l ⁴ +16l ² +20      ₄ 4+l ²     1+l ²     16Pe ²       ₂              16Pe ²

(4+l ² )(1+l ² ) ^{- π Rp} l ² (1+l ² )(4+l ² ) ^+π    l ²       l ^{2    +} 9l ^{2 =ARp - BRp+C+} 9l ^{2 =0.} (23)

Очевидно, что уравнение (23) не содержит действительных корней при Pe > l (9B ² - 36AC)/64A, то есть, например, для l = 3 при Pe > 4.2.

Для проверки сходимости в качестве первого теста было выбрано визуальное сравнение нейтральных кривых для разных значений N . Для этого на рисунке 10 приведены нейтральные кривые для монотонной и колебательной мод возмущений. На рисунке прослеживается изменение вида нейтральной кривой при увеличении количества базисных функций. При N = 6 кривая обрывается, так как исчезает монотонное решение. Для остальных случаев решение существует в области рассматриваемых значений числа Пекле. Видно, что при N > 24 решения практически совпадают с точностью до шага по числу Пекле (шаг равнялся ∆Pe= 0.005).

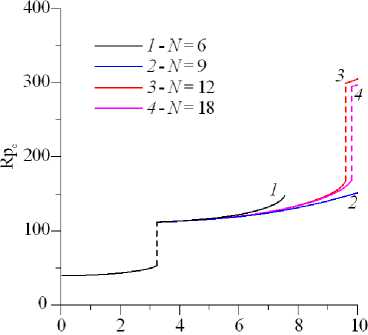
Рис. 10. Нейтральные кривые на плоскости (Pe,Rp c ) для разного числа N базисных функций в разложении; кривые построены для монотонной моды неустойчивости (сплошные линии, на которых штрихами показаны разрывы) при l = 1 , a = 5 , b = 5

( a )

95 п

( a )

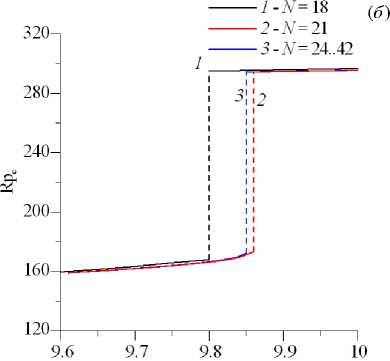
У-Л'=12 2-.¥=18 5-.¥=21

( б )

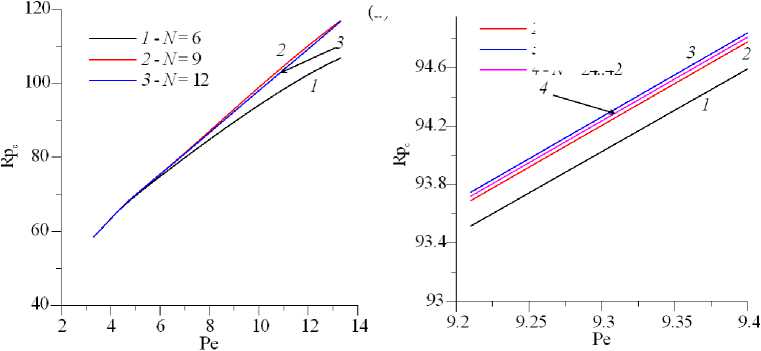
Рис. 11. Нейтральные кривые на плоскости (Pe,Rp c ) для разного числа N базисных функций в разложении; кривые построены для колебательной моды неустойчивости при l = 1 , a = 5 , b =5

На рисунке 11 продемонстрировано изменение формы нейтральных кривых для колебательной моды возмущений при изменении числа N функций в разложении. Видно, что, как и следовало ожидать, колебательная мода менее чувствительна к его изменению: при N > 24 кривые неотличимы друг от друга. Зависимости на рисунках 10, 11 дают представление о сходимости метода и даже позволяют определить некоторый предел для величины N . Однако такой подход менее объективен, чем анализ зависимости критического значения числа Релея–Дарси и частоты нейтральных возмущений от N при фиксированном значении других параметров. Такие зависимости для разных l содержат рисунки 12, 13. Из рисунка 12 видно, что четное и нечетное числа базисных функций приближают истинное значение с разных сторон (четное N дает заниженное значение, нечетное N — завышенное). Уверенная сходимость для монотонной моды наблюдается при N > 30. Кривые сходимости для колебательного режима представлены на рисунке 13.

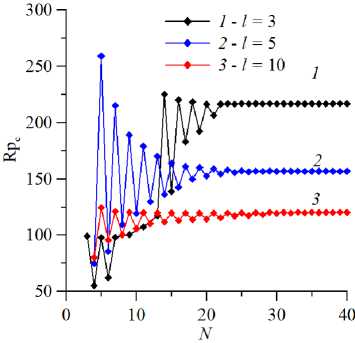
Рис. 12. Кривая сходимости критического значения числа Релея–Дарси в зависимости от N – числа базисных функций в разложении; расчет сделан для монотонной моды неустойчивости при разных значениях геометрического параметра l и Pe = 5 , a = 5 , b = 5

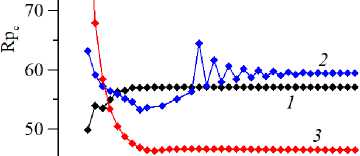
—♦— 1-1 = 3

—»— 2-1 = 5

—•— 3-/= 10

0       10      20      30      40

N

( a )

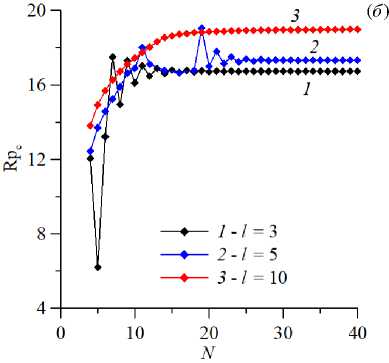
Рис. 13. Кривые сходимости критического числа Релея–Дарси ( a ) и частоты нейтральных возмущений ( б ) в зависимости от числа N базисных функций в разложении; расчет сделан для колебательной моды неустойчивости для разных значений геометрического параметра l при Pe = 5 , a = 5 , b = 5

Рисунок 13 демонстрирует лучшую в целом сходимость колебательной моды, однако для l = 5 она оказалась достаточно медленной. Из анализа рисунков 12 и 13 следует вывод, что для уверенной сходимости метода нужно использовать число базисных функций N > 35. Во всех основных расчетах было использовано N = 40 базисных функций.

• 7.    Заключение

Исследовано возникновение конвективного течения в находящейся в поле силы тяжести замкнутой прямоугольной области пористой среды в присутствии принудительного горизонтального течения и вертикального перепада концентрации с учетом иммобилизации примеси. Получено, что, в зависимости от соотношения сторон области и скорости внешнего фильтрационного течения, конвекция в такой конфигурации может осуществляться как монотонным, так и колебательным образом. Получены критерии перехода от монотонного режима к колебательному. Построены карты режимов существования колебательной неустойчивости на различных плоскостях параметров задачи. Изучено влияние иммобилизации на возбуждение конвективного течения, показано, что она приводит к стабилизации режима однородной горизонтальной фильтрации и существенно влияет на частоту возникающих колебаний. Показано, что результаты расчетов для l > 8 близки к известным результатам из [19], полученным для бесконечного горизонтального слоя.

Работа выполнена за счет гранта Российского научного фонда, проект № 20-11-20125 20125/).