Концептуально-онтологические аспекты множественности предка в информационных моделях "сущность-связь"

В проектировании автоматизированных систем важное место занимают информационные модели (ИМ), характеризующие используемые данные в создаваемой системе. ИМ разрабатываются на различных уровнях абстракции: концептуальные модели ориентированы на выявление информационных потребностей системы; логические (внутренние) – на реализацию баз данных (БД), обслуживающих эти потребности. ИМ концептуального уровня абстракции отражают онтологические аспекты создаваемой системы и должны позволять разработчикам представлять знания о предметной области (ПрО) в виде концептуальной схемы: классы сущностей, их атрибуты, связи, правила и ограничения [1, 2].

Распространение получил класс ИМ «сущность-связь» ( Entity-Relationship Model – ER -модель), как концептуальная основа логических моделей БД [3], ориентированных на реляционные и объектно-ориентированные БД. Эти модели положены в основу промышленных стандартов ( IDEF1x, UML и др.) и широко применяются в настоящее время [4–7].

ER-модели наглядно задают классы сущностей и связи между ними, т.е. структурные ограничения целостности данных. Вместе с тем они не отражают некоторые важные особенности ПрО, в отличие от онтологических моделей [7, 8]. Ввиду высокой понятности, лако- ничности и лёгкой реализуемости ER-моделей замена их на онтологическую модель применительно к БД считается нецелесообразной [9]. ER-модели являются неотъемлемым средством проектирования БД [10, 11].

Целью данной работы является исследование отношений между классами сущностей и обусловленных ими ограничений целостности в ER -моделях при проектировании БД. Указанные отношения связаны с межклассовыми отношениями типа «предок-потомок» [12], названными здесь отношениями множественного предка (МП).

1 Отношения множественного предка

Предметом исследования являются межклассовые отношения типа «предок-потомок», которые непосредственно не отражаются в ER-моделях.

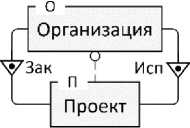
Рисунок 1 - Простой пример МП-отношения

Простейший случай подобных отношений может возникать в моделях, содержащих два класса сущностей с двумя связями между ними (см., например, рисунок 1). Здесь класс Организация задаёт множество экземпляров - конкретных организаций, а класс Проект - множество конкретных проектов. Две связи типа «один-ко-многим» - Зак (заказывает) и Исп (исполняет) - задают отношения «предок-потомок» между сущностями. Конкретная организация может быть заказчиком и исполнителем нескольких проек- тов, но каждый проект имеет одну организацию-заказчика и одну организацию-исполнителя. Пусть при этом имеет место ограничение: одна и та же организация не может быть одновременно заказчиком и исполнителем одного и того же проекта. Данное ограничение никак не отражается традиционными средствами в рассматриваемой модели, т.е. ничто не препятствует, чтобы некоторый экземпляр Проекта ссылался на один и тот же экземпляр Организации и как на заказчика, и как на исполнителя. Налицо «нарушение целостности» - аномалия, потенциально допускающая несогласованность и требующая введения дополнительных семантических пояснений к ER-модели. Это обстоятельство отражено на схеме с помощью пунктирной линии, концевой кружок которой задаёт направление от класса-предка к классу-потомку. Это ограничение целостности можно назвать МП-ограничением, которое может возникать в ER-моделях, имеющих следующие структурные особенности (МП-отношения):

• ■    имеется два класса сущностей, находящихся в отношении «предок-потомок»;

• ■    имеется две или более восходящих связей, ведущих от потомка к предку.

Опыт проектирования ER -моделей БД свидетельствует, что МП-отношения, сопровождаемые МП-ограничениями, часто возникают в ходе построения глобальной ER -модели путём композиции локальных моделей.

На рисунке 2 эта ситуация иллюстрируется на простом примере. Здесь локальная модель « а » задаёт отношение «один-ко-многим» между сущностями Спец (специальность) и Студент : на каждой конкретной специальности может обучаться несколько студентов, но каждый конкретный студент обучается на одной специальности. Аналогичным образом локальная модель « б » утверждает: каждая специальность может включать несколько предметов, но каждый предмет относится к одной специальности. Локальная модель « в » задаёт отношение «многие-ко-многим» между сущностями Студент и Предмет с помощью сущности-пересечения Сдача : каждый конкретный студент может сдать несколько конкретных предметов, а каждый конкретный предмет может быть сдан несколькими конкретными студентами. Экземпляр сущности Сдача соответствует паре «конкретный студент - конкретный предмет». Модель « г » на рисунке 2 представляет собой композицию моделей « а », « б » и « в », содержащую все отношения между сущностями Спец , Студент , Предмет , Сдача .

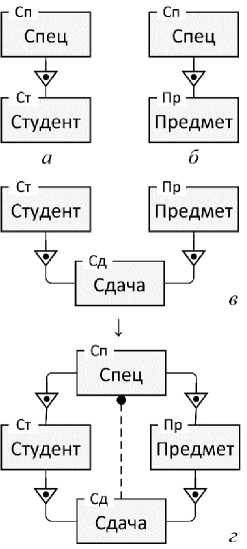
Рисунок 2 - Возникновение МП-отношения в результате композиции моделей

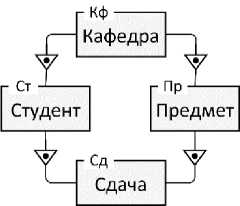
Рисунок 3 - МП-отношение без МП-ограничения

Модель «г » не может учесть те отношения, которые выходят за пределы локальных моделей и относятся к композиции в целом (целое не есть простое объединение частей). Здесь никак не отражено то естественное ограничение, что студент должен сдавать предметы только своей специальности. Если взять конкретный экземпляр сущности Сдача , то для него, согласно модели, существует единственный экземпляр-предок в сущности Студент , для которого существует единственный экземпляр-предок в сущности Спец . Для того же самого экземпляра сущности Сдача существует единственный экземпляр-предок в сущности Предмет , для которого существует единственный экземпляр-предок в сущности Спец . При этом ничто в модели не гарантирует, что в обоих случаях это будет один и тот же экземпляр сущности Спец . Т.е. складывается аномалия, потенциально допускающая несогласованность и требующая введения соответствующих семантических ограничений. На рисунке она отмечена пунктирной линией с концевым кружком. Тёмная заливка кружка (в отличие от светлой на рисунке 1) указывает на то, что экземпляры предка, соответствующие одному потомку, должны совпадать.

Необходимость различать МП-отношение и МП-ограничение обусловлена тем, что не всегда первое влечёт за собой второе. На рисунке 3 приведена иллюстрация МП-отношения, не сопровождающегося МП-аномалией. Здесь класс Кафедра включает множество экземпляров-кафедр, за каждой кафедрой может быть закреплено много студентов и много предметов. При этом студенты изучают и сдают предметы, которые закреплены за разными кафедрами. Таким образом, здесь не накладываются ограничения на экземпляры предков одного потомка, т.е. в отличие от примера на рисунке 2 не требуется, чтобы для одной сдачи кафедра сдавшего студента всегда совпадала (или, наоборот, не совпадала) с кафедрой сданного предмета.

Таким образом, МП-целостность характеризуется наличием МП-отношения и МП-ограничения. МП-ограничение - это некоторое требование, предъявляемое со стороны ПрО к множеству экземпляров предков каждого экземпляра потомка в МП-отношении. В простых случаях - это требование совпадения или несовпадения экземпляров предков. Возможны и более сложные требования.

2    Формализация

Пусть ER -модель ERM = { E, R } - множество сущностей E и бинарных связей R типа «предок-потомок». Другие виды связей («многие-ко-многим»; n -арные, n > 2; и др.) могут быть представлены с помощью бинарных связей.

Линия восходящего родства (ЛВР)

L = Ed ^ E1 — ... — Em — Ea (1) представляет собой последовательность сущностей ED, Ei, ..., Em, EA, где m > 0, в которой сущность E 1 является предком сущности ED, а последующая сущность Ei+1 является предком предшествующей сущности Ei (обозначается как Ei —*Е)+1). Для m = 0 выражение (1) имеет вид L = ED—*EA. Сущности ED и EA, соответственно сущность-потомок и сущность-предок в ЛВР L, можно записать так:

E d = _ L , E a = * L , (2) где символы «_» и «^» обозначают операции извлечения из ЛВР потомка и предка.

Если сущность E i ₊ 1 является «множественным» предком сущности E i (через несколько параллельных связей типа «предок-потомок»), то в записи E i —• E i ₊ 1 требуется уточнение:

I - E i + 1 , (3)

где R i – идентификатор используемой в ЛВР связи «предок-потомок».

ЛВР как функция экземпляров потомка. Если все связи, образующие ЛВР L, не допускают «сирот», то каждому экземпляру eD сущности-потомка ED всегда соответствует один и только один экземпляр eA сущности-предка EA, т.е. имеет место функциональная зависимость л L (eD) = eA, eD е Ed, eA е Ea . (4)

«Сиротабельные» связи. Пусть на ЛВР присутствуют связи, допускающие «сиротство», т.е. такие экземпляры сущностей потомков, у которых нет соответствующих экземпляров сущностей предков. В этом случае выражение (1) будет записано так:

L = Ed^Ei^ ... E^Ek +1^ ... EmEmEA,EA , (5) где Ek—EEk+1 соответствует «сиротабельной» связи, которая находится ближе всего к сущности-потомку ED. На экземпляре-сироте происходит «обрыв» экземпляра ЛВР. Это означает отсутствие экземпляра eA сущности-предка EA. В таких случаях можно дополнить множества экземпляров сущностей Ek+1, ..., Em, EA фиктивными null-экземплярами, полагая, что в случае «обрыва» экземпляра ЛВР он продолжается цепочкой null-экземпляров, т.е. в этом случае лL (eD) = null . (6)

Для учёта подобных случаев вводятся функции-предикаты ifnull ( e ) и ifnotnull ( e ) , у которых результат «истина», если e соответственно является или не является null -экземпляром, и «ложь» в противном случае.

МП-отношение - это совокупность двух или более различных ЛВР L 1 , L ₂, ..., имеющих одинаковых потомков и одинаковых предков, т.е. ведущих разными путями от общего потомка к общему предку:

M = { L 1 , L ₂, ... }, _ L 1 = _ L 2 = ... , л L 1 = л l ₂ = . . (7)

МП-ограничение - это ограничение, заданное на МП-отношении M в виде

V e D , e D е E d , Pr ( M ) = f ( л l 1 ( e D ), л l 2 ( e D ), . ) , (8) где V - квантор всеобщности; Pr ( M ) - предикат МП-целостности (МП-предикат), т.е. некоторая логическая функция f , задающая условие, которое должно выполняться для обеспечения целостности. Таким образом, МП-ограничение накладывается на совместные значения экземпляров предка, полученные для одного экземпляра потомка через различные ЛВР.

МП / МП-ограничение (положительное / отрицательное МП-ограничения) - частные случаи, когда МП-предикат Pr ( M ) задан соответственно в виде равенства или в виде неравенства экземпляров предка:

Pr( M )⁺ : V ( L i е M , L j е M , i * j ) л L i = л L j , (9)

Pr( M ) ’ : V ( L е M , L j e M , i * j ) л L i * * L j , (10) т.е. МП ⁺ -ограничение для каждого экземпляра потомка требует одних и тех же экземпляров предка по всем ЛВР, а МП ' -ограничение - различных. В реальных ситуациях могут требоваться более сложные логические условия (смешанные МП-ограничения).

Чтобы формализовать МП-целостность, нужно задать: множество ЛВР (7), составляющих МП-отношение; МП-предикат (8), определяющий МП-ограничение для МП-отношения.

3    Примеры 3.1    Положительные МП-ограничения в отсутствие сирот Рисунок 4 - Пример МР+-целостности

На рисунке 4 представлен пример задания положительного МП-ограничения, основанного на двух четырёхзвенных ЛВР. Модель отражает результаты сдачи студентами предметов. Каждая сдача соответствует одному студенту, который прикреплён к одной студенческой группе одной специальности. С другой стороны, каждая сдача соответствует одному предмету, который соответствует одному циклу, также одной специальности. Представленные в модели связи «один-ко-многим» не допускают сирот (тёмные кружки в символах связи). Отношение МП-целостности задано штриховой линией, идущей от потомка к предку. Тёмный кружок, указывающий на предка, означает положительную МП-целостность. Таким образом, МП⁺-целостность СдлСп обеспечивается по двум ЛВР:

СдлСп = { L 1 = Сд .Ст .Гр <п, L 2 = Сд .Пр .Цк .Сп } , Pr (Сд^лСп ): л L 1 = л l ₂ , (11) т.е. требуется, чтобы для каждой сдачи совпадали специальности сдавшего студента и сданного предмета. В данном случае задание МП-целостности на графической модели (рисунок 4) исчерпывающе характеризует МП-ограничение: в модели имеется всего две ЛВР, и формальное представление (11) не несёт новой информации по сравнению со схемой. В более сложных случаях графическая нотация бывает недостаточна для задания деталей МП-целостности и требуется дополнительная формальная спецификация.

• 3.2    Положительные МП-ограничения в случае допустимости сирот

На рисунке 5 представлен пример задания МП⁺-целостности при наличии связи, допускающей сирот (светлый кружок в символе связи). В отличие от модели на рисунке 4 здесь допустимы студенты, которые (временно) не прикреплены к студенческой группе (например, находятся в академическом отпуске). При этом каждый студент относится только к одной специальности (дополнительная связь от сущности Спец к сущности Студент). В этой модели присутствуют два перекрывающихся отношения положительной МП-целостности: СтЛСп и СдлСп . МП-целостность СтлСп задаёт согласованность специальности обучения студента и специальности группы, к которой прикреплён студент. Она базируется на двух ЛВР:

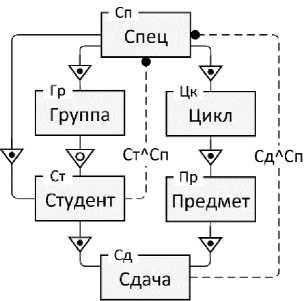
Рисунок 5 - Пример сложной МР+-целостности

СтЛСп = { L 1 = Ст .Сп, L 2 = Ст^Гр^Сп } . (12)

Предикат Pr (СтЛСп) должен быть истинным только в двух случаях:

• ■    если студент ст₀ не прикреплён ни к какой к группе;

• ■    если студент ст₀ прикреплён к группе, у которой специальность группы ^Л L ₂ (ст₀) совпадает со специальностью студента л l i (ст₀) .

• 3.3    Пересекающиеся МП-отношения

Таким образом, предикат имеет вид

Pr (Ст^лСп) : ifnotnull (л L гр ) >  ( л l 1 = л l ₂ ) ,                                                         (13)

где L _гр = Ст—° Гр , а « > » обозначает операцию импликации, или в эквивалентной записи:

Pr (СтлСп) : ifnull (л L гр ) | ( л l i = л L 2 ) ,                                                                   (14)

где « | » обозначает операцию дизъюнкции («или»).

МП-целостность СдлСп (рисунок 5) задаёт согласованность специальностей по различным ЛВР от потомка Сдача к предку Спец . В модели содержится три ЛВР, относящихся к этому МП-отношению:

L з = Сд «Пр «Цк «Сп , L 4 = Сд «Ст «Сп , L 5 = Сд^Ст^Гр^Сп .        (15)

Таким образом, рассматриваемая МП-целостность базируется на трёх ЛВР:

СдлСп = { L з , L 4 , L 5 }.                                        (16)

МП-предикат Pr (СдлСп) должен проверять равенство экземпляров предков, полученных вдоль этих трёх ЛВР, и должен быть истинным в следующих случаях:

• ■    если в сдаче сд сдавший студент не прикреплён к группе и при этом обучается на специальности л l ₄ (сд) , совпадающей со специальностью сданного предмета л L ₃ (сд) ;

• ■    если в сдаче сд сдавший студент прикреплён к группе, при этом его специальность л L ₄ (сд) совпадает со специальностями группы л l ₅ (сд) и сданного предмета л L ₃ (сд) .

• 3.4    Отрицательные МП-ограничения

Следует учесть, что ЛВР L ₄ включает ЛВР L ₁ , ЛВР L ₅ включает ЛВР L ₂ и при этом соблюдается МП-целостность СтлСп , основанная на ЛВР L ₁ и L ₂ . В этих условиях для достижения целостности СдлСп достаточно потребовать, чтобы в сдаче сд специальность сдавшего студента совпадала со специальностью сданного предмета, т.е. достаточно контролировать две ЛВР - L ₃ и L ₄ :

СдлСп = { L з , L 4 }, Pr (СдлСп) : л l 3 = л l 4 .                          (17)

Таким образом, наличие пересекающихся ЛВР в положительных МП-отношениях может упростить МП-предикаты.

В примере на рисунке 5 ЛВР (17), относящиеся к СдлСп , полностью включают ЛВР (12), относящиеся к СтлСп . В этих условиях может показаться, что МП-целостность СдлСп , основанная на (17), автоматически влечёт за собой МП-целостность СтЛСп , что неверно. Это было бы так, если бы у каждого студента обязательно была хотя бы одна сдача (связь Студент-Сдача не допускала бы предков без потомков, т.е. была бы тёмная заливка у треугольника в символе связи). Однако в этой модели допустимы студенты, не имеющие сдач (светлая заливка в треугольнике связи), поэтому такие студенты выпадают из-под контроля со стороны МП-целостности СдЛСп .

Особенности обеспечения отрицательной МП-целостности, требующей различных экземпляров МП-предков для одного МП-потомка по различным ЛВР, представлены примером, показанном на рисунке 6. Модель отражает две роли участия людей (сущность Персона) в диссертации на соискание учёной степени кандидата наук (сущность Диссертация), а именно: автор-диссертант (сущность Автор) и научный руководитель (сущность Научрук). У конкретной диссертации должен быть единственный автор и единственный научный руково- дитель. Конкретная персона может быть автором или научным руководителем. Бинарная связь типа «может быть», или «условная», является частным случаем связи типа «один-ко- многим»: одному экземпляру сущности-предка может соответствовать ноль или один экзем пляр сущности-потомка.

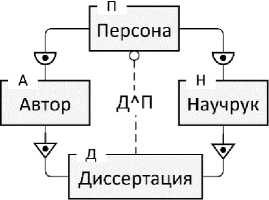
Рисунок 6 - Пример отрицательной МР-целостности

В используемой графической нотации эта связь изображена в виде полукруга, направленного к потомку. МП-целостность Д^ЛП является отрицательной, о чём свидетельствует светлый кружок, указывающий направление к МП-предку. Эта целостность требует, чтобы для каждой диссертации её автор и научный руководитель были разными персонами:

ДЛП = { L 1 = Д -А .П, L ₂ = Д -Н -П }, Pr (ДЛП) : л L 1 * ^л L 2 .(18)

Если предположить, что у диссертации не обязательно должен быть научный руководитель, т.е. связь от Н к Д является «сиротабельной», допускающей сирот ( L _Н = Д—°Н), то МП-целостность будет выглядеть так:

ДЛП = { L 1 = Д^А^П, L 2 = Д ■ Н ■ П }, Pr (ДЛП) : ifnull (л L н ) | ^л L 1 * л l 2 .        (19)

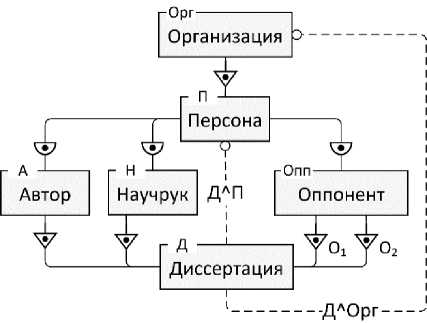
Рисунок 7 - Пример сложной отрицательной МР-целостности

На рисунке 7 представлен более сложный пример, содержащий два взаимосвязанных ограничения отрицательной МП-целостности. В отличие от модели на рисунке 6 здесь дополнительно присутствует Оппонент, как класс Персоны , а также сущность Организация, как предок Персоны . У диссертации должно быть два оппонента, что обеспечивается связями О 1 и О 2 . Каждая Организация может содержать насколько аффилии-рованных Персон , каждая Персона должна быть аффилирована с одной Организацией .

МП-ограничение ДЛП в данном случае требует, чтобы для одной и той же диссертации её автор, научный руководитель и оба оппонента были

(

1 = Д  А   П

2 = Д   Н   П     ^⎫

разными персонами:

Д^лп =

L з = Д^ Опп^П ^{- Р}г⁽Д^ЛП) : ^{V (} L i , L j , i , j = 14, i * j )

л L i * л L j .

4 = Д    Опп П ⎭

Для предиката Рг(Длп) требуется выполнение следующих условий:

Pr (ДЛП) : л L 1 * (л L 2 , Л L ₃ , л l ₄) , л l 2 * (л l ₃ , л L ₄) , л L ₃ * л l ₄ .

Для МП-ограничения ДЛОрг требуется, чтобы оппоненты диссертации были из разных организаций, не совпадающих с организациями автора и научного руководителя (при этом автор и руководитель могут быть из одной организации). Формально это требование можно записать так:

= Д А П

ДЛОрг = 4

⎪    6 = Д   Н   П   Орг     ⎪ L 7 = Д^ Опп-П-Орг Г - Рг<ДЛОрг> : Л L 7 * Л L 8 - V ( L i , L j j = ((7, 8) Л L i * Л L j   (22) ⎩ 8 = Д    Опп  П  Орг ⎭

Для предиката Pr (Д^ЛОрг) требуется выполнение следующих условий:

Pr (ДЛОрг) : a l 7 * л l ₈ , л l ₅ * (л l 7 , л l 8 ) , л l ₆ * (л l 7 , л l 8 ) .                     (23)

Следует учесть взаимодействие ограничений ДЛП и ДЛОрг , а именно, что ЛВР, входящие в ДЛП , являются частью ЛВР ДЛОрг . Любые экземпляры персоны заведомо различны, если они аффилированы с разными экземплярами организации. Поэтому выполнение требования различной аффилиации оппонентов л l ₇ * л l 8 в (23) автоматически влечёт за собой выполнение требования различных персон оппонентов л L ₃ * л l 4 в (21). Аналогичным образом выполнение требований л l ₅ * (л l ₇ , л l 8 ) и л l 6 * (л l ₇ , л l 8 ) автоматически влечёт за собой выполнение требований л l 1 * (^Л L 3 , л L 4 ) и л L 2 * (л L 3 , л L 4 ) .

Эти обстоятельства упрощают предикат Pr (ДЛП) :

Рг(Длп) : л l 1 * л l 2 ,                                        (24)

т.е. при наличии предиката Pr (ДЛОрг) предикат Pr (ДЛП) должен контролировать лишь то, что экземпляры автора и научного руководителя одной диссертации соответствуют различным экземплярам персоны.

Таким образом, наличие пересекающихся ЛВР в МП-отношениях может упростить ограничения. Например, если дополнительно предположить, что автор и руководитель одной диссертации обязательно должны быть из разных организаций, то ограничения ДЛОрг автоматически обеспечат все ограничения ДЛП и надобность в ДЛП отпала бы вовсе.

• 3.5    Расщепление МП-ограничений

Если некоторая МП-целостность M имеет предикат в виде конъюнкции двух или более логических выражений Pr ( M ) = ( P 1 , P ₂ , .„) , то её можно представить в виде эквивалентной совокупности двух или более МП-целостностей, заданных на том же МП-отношении.

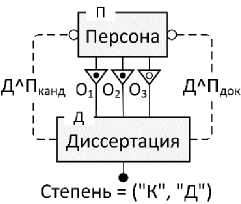
Рисунок 8 - Пример расщеплённого МР-ограничения

На рисунке 8 представлен пример ER -модели, отражающей участие персон в качестве оппонентов диссертации, для чего класс Персона связан с классом Диссертация тремя связями - О 1 , О₂ , О₃ . Отрицательная МП-целостность ДЛП (не показана на рисунке) призвана обеспечить требование: оппоненты одной диссертации должны быть разными персонами. При этом (в отличие от примера на рисунке 7) учитывается, что для кандидатской диссертации требуется два оппонента, а для докторской - три. Для этого связь О 3 «третий оппонент» допускает сирот (светлый кружок). Вид конкретной диссертации («кандидатская» или «докторская») задаётся значением атрибута Степень .

МП-ограничение ДЛП расщеплено на два МП-ограничения для случаев кандидатской и докторской диссертаций соответственно:

ДЛП канд контролирует кандидатские диссертации, проверяя несовпадение первого и второго оппонентов и отсутствие третьего:

ДЛП канд = { L 1 = Д^П, L 2 = Д^П, L 3 = Д^>П },                   (24)

Pr (ДЛП_ка нд ): ( _ L 1 . Степень = "К" ) ^ ( л l 1 * л l 2 , isnull (л L 3 ) ) .

ДЛП_док контролирует докторские диссертации, проверяя присутствие третьего и несовпадение первого, второго и третьего оппонентов:

ДЛП док = { L 1 = Д^П, L 2 = Д^П, L 3 = Д^П },                  (25)

Pr (ДЛП док ): ( _ L 1 . Степень = "Д" ) ^ ( isnotnull (л L 3 ), л L 1 * л l 2 , л l 1 * л l 3 , л l 2 * л l 3 ) .

Таким образом, расщепление МП-ограничений в некоторых случаях может сделать представление МП-целостности в ER -модели более понятным.

Заключение

Введено понятие МР-целостности, возникающее при наличии в ER -модели определённых структурных особенностей – МП-отношений, – когда имеется несколько цепочек связей от некоторого класса-потомка к некоторому классу-предку. На МП-отношениях могут задаваться МП-ограничения, отражающие особенности ПрО, которые накладываются на множество экземпляров предков каждого экземпляра потомка. Введена графическая нотация для обозначения МП-целостности на ER -диаграмме.

Выполнено формальное описание МП-целостности в символьной нотации на основе введённой системы взаимоувязанных определений:  ЛВР; «сиротабельная» связь;

МП-отношение; МП-ограничение (в т.ч. частные случаи – положительное и отрицательное МП-ограничения); МП-предикат. Это позволяет задавать формальные концептуальноонтологические спецификации правил обеспечения МП-целостности, дополняющие и уточняющие графическую нотацию.

На примерах ER -моделей продемонстрированы особености задания МП-целостности в графической и в символьной нотациях. Рассмотрены примеры положительных и отрицательных МП-ограничений. Показано взаимное влияние нескольких МП-ограничений с пересекающимися ЛВР, учёт которого позволяет в ряде случаев упростить МП-предикаты. Показано, что расщепление МП-ограничений со сложными МП-предикатами даёт возможность сделать представление МП-целостности более понятным.