Конечномерная аппроксимация управлений в задачах оптимизации линейных систем

Задачи на экстремум нормы конечного состояния линейной управляемой системы имеют давнюю историю, но до сих пор сохраняют определенный уровень актуальности и потенциал научного интереса. Задача на минимум нормы в силу своей выпуклой структуры обеспечена в настоящее время эффективными методами решения на основе нелокальных улучшений с использованием матричной сопряженной системы [1; 5; 10].

Задача на максимум нормы конечного состояния является многоэкстремальной, что существенно затрудняет ее глобальное решение. Разработанные методы ориентированы на улучшение экстремальных управлений и построены на основе условий глобальной оптимальности [2; 7; 8]. Поскольку вычислительная проверка выполнения этих условий до сих пор проблематична, то известные методы реализуют, вообще говоря, ослабленные, неполные версии критериев оптимальности. Такая ситуация не позволяет обосновать получение глобального решения, т. е. содержит эвристические элементы. Иными словами, проблема максимизации нормы еще открыта для дополнительных исследований.

В данной работе задачи на экстремум нормы конечного состояния для линейной системы рассматриваются в рамках технологии параметризации управляющей функции [4; 6; 11]. При этом аппроксимация проводится в классе кусочно-постоянных функций на заданной сетке узлов промежутка времени. В результате задача оптимального управления преобразуется в конечномерный вариант на экстремум выпуклой квадратичной функции на гиперкубе.

Полученная задача на минимум допускает решение за конечное число итераций [9]. В целях упрощения процедуры решения предлагается без-итерационный алгоритм для двумерной задачи (минимум параболоида на квадрате), использующий геометрическую интерпретацию.

Глобальное решение конечномерной задачи на максимум элементарно реализуется через полный либо специализированный перебор заданного набора вершин гиперкуба. Таким образом, в рамках представленного подхода исходная невыпуклая задача аппроксимируется аналогичной конечномерной задачей выбранной размерности, которая гарантированно решается в глобальном смысле процедурой приемлемого конечного перебора.

Проведена апробация рассмотренной технологии решения на иллюстративных задачах.

• 1    Постановка задачи

Введем переменные t е [t0, T] — время, u(t) е R — управление, x(t) е R” — фазовое состояние, связанные линейной системой x = A (t) x + b (t) u,       x (t0) = x0

с непрерывными на [ t ₀, T ] функциями A ( t ) е R ” ^x ” , b ( t ) е R ” .

Множество V допустимых управлений содержит кусочнонепрерывные функции u ( t ) со стандартным ограничением

u(t) е [u-, u+],        t е [t0, T].(2)

На множестве V определим терминальный функционал (норма конечного состояния)

Ф( u) = 1 {x (T), x (T))(3)

и рассмотрим соответствующие задачи на экстремум (минимум или максимум).

Проведем преобразование этих вариационных задач к конечномерным на основе простейшей процедуры параметризации допустимых управлений.

Введем на отрезке [ t ₀, T ] равномерную сетку узлов t_t = t ₀ + th , i = 0, m

, ^{T —} t o с шагом h =---0

.

m

Выделим ячейки Tj = (tj—1, tj ], j = 1, m и определим характеристиче- ские функции

X j ⁽ t ) =

' 1, t е T , 4 t e T j .

Пусть y = ( y 1 ,..., y_m ) — набор параметров. Образуем семейство управлений

u ( t , y ) = £ y j- X j ( t ),     t е [ 1 0 , T ]

j = 1 и введем подмножество допустимых управлений

V = { u ( • , y ): y j е [ u — , u + ], j = 1, m }.

Пусть x ( t , y ), t е [ 1 ₀, T ] — решение фазовой системы (1), соответствующее управлению u ( t , y ). Тогда

x ( t , y ) = x ( t ,0) + ^Гу/( t ), t е [ 1 0 , T ]               (4)

j = 1

где x^j ( t ) — решение фазовой задачи Коши

5с = A ( t ) x + b ( t ) x j ( t ),         x ( 1 0 ) = 0.

Рассмотрим функционал Ф ( и ) на множестве управлений V 1 . Используя представление (4), получаем формулу

Ф1(у) = Ф(0) + (d, у) + 2(Ху, Ху), в которой d — m -вектор с компонентами Хх(T, 0), xj (T)^, j = 1, m,

X — ( n х m ) - матрица со столбцами х^j ( T ), j = 1, m .

Отметим, что квадратичная функция Ф 1 ( у ) является выпуклой, что позволяет квалифицировать соответствующие экстремальные задачи на множестве простейшей структуры: у е [ и - , и ₊ ].

• 2    Задача на минимум нормы конечного состояния

Рассмотрим задачу

Ф ( и ) = 2 ( х ( T , и ), х(T , и )) ^ min,           и е V .         (4)

После параметризации получаем специальную задачу выпуклого про граммирования относительно вектора у = (у 1,..., ym)

Ф1(у) = Ф(0) + (d, у) + 2 (Ху, Ху) ^ min, у е [и_, и + ].    (5)

Такая квадратичная задача допускает решение за конечное число итераций [9].

Выделим частные случаи задачи (5) относительно размерности m , которые решаются по явным формулам без итерационного процесса .

Пусть m = 1, т. е. задача (4) решается на множестве const-управлений и ( t ) = у 1 , t е [ 1 ₀, T ]. Соответствующая одномерная задача (5) имеет вид (минимум выпуклой параболы на отрезке)

Ф1(у 1) = Ф(0) + у^х(T, 0), х 1(T)) + 2у2(х‘(T), х 1(T)) ^ min, у1 е [и_, и + ].

При условии х ¹ ( T ) ^ 0 определим стационарную точку

* __ ( х(T , 0), х 1 ( T )) ^у 1 =   ( х 1 ( T ), х 1 ( T)У

Тогда решение одномерной задачи представляется очевидным образом

		г * у 1,	у ** е [ и _ , и + ]
У 1min	_	и - ,	*     _ у 1 <  и - ,
		и + ,	* у 1 >  и + .

Пусть, далее, m _ 2, т. е. задача (4) решается на множестве управлений

I У1,    t G [t0, t 1], u (t) = 4

[ У 2, t G (t1, T1, с фиксированной точкой переключения 11 =

1 0 + T

•

Соответствующая двумерная задача (5):

минимизация функции двух переменных Ф 1 ( у 1 , у ₂) на квадрате

Y = ^{( У 1 , У 2^): У / ^G [ u - , u + L i = ^1,2}.

Предположим, что матрица X g R^{n х 2} имеет полный ранг, т. е. матрица Грама X T X положительно определена. Тогда единственная стационарная точка у * = ( у * , у 2 ) функции Ф 1 ( у ) находится из линейной системы

7Ф , ( у ) = d + X T Ху = 0.

Это точка минимума функции Ф1(у) на R2. При этом линии уровня функции Ф1( у) — эллипсы с центром в точке у *.

Проведем аналитическое решение задачи минимизации параболоида Ф 1 ( у ) на квадрате Y , используя информацию о положении точки у * и геометрическую интерпретацию задачи на основе линий уровня целевой функции.

Если у * g Y , то получено решение двумерной задачи на минимум:

у ^min = у \

Проанализируем основной случай у * £ Y .

Возможные ситуации нарушения ограничения по одной переменной:

1) у * <  и - , у 2 g [ и - , и ₊ ]    ^ решить одномерную задачу

Ф 1 ( и _ , у 2 ) ^ min, положить у !™ = и - , у ^mn = у ₂ ;

2) у * >  и + , у 2 G [ и - , и + 1     ^

Ф 1 ( и + , у 2 ) ^ min, положить у ;™ = и ₊ , у mⁱⁿ = у + ; 3) у * G [ и - , и + 1, у 2 <  и - ^

Ф 1 ( у 1 , и - ) ^ min , положить y^’n = у - , у ₂ ^min = и - ; 4) у * G [ и - , и + 1, у * >  и + ^

Ф 1 ( у 1 , и + ) ^ min, положить у ₁‘”^1П = у + , у m¹ⁿ = и ₊ .

у 2 G [ и - , и + 1    ^ у 2 ,

решить одномерную задачу у 2 G [ и -, и +1    ^      у 2+ ,

решить одномерную задачу у1 G [ и -, и + 1    ^      у- ,

решить одномерную задачу у1 G [ и -, и + 1    ^      у+ ,

Возможные нарушения ограничений по двум переменным у 1 , у ₂:

• 5)    у 1 <  и - , у ₂ <  и - ^ решить две одномерные задачи

Ф1( и -, У 2) ^ min, у 2 е [ и _, и+]   ^     у 2

Ф1( У1, и -) ^ min, yi е [ и _, и + ]   ^     у-, положить

z min minx _ ( и - , у 2 ), ( у 1 , у 2 ) = 1 , _     , К у 1 , и - ),

Ф 1( и - , у 2 ) ^Ф 1( у 1 - , и - ), Ф 1( и - , у 2 ) ^Ф 1( у 1 - , и - ),

• 6)    у* > и+, у2 > и , > решить две одномерные задачи Ф1( и +, у 2) ^ min, у 2 е [ и _, и+]   ^

Ф1( У1, и +) ^ min, у1 е [ и _, и + ]   ^

положить

( ч"" . у 2mi" ) = 1 ( и ,у у + )’ К У 1 , и + ),

Ф 1( и + , У 2+) ^Ф 1( У 1 + , и + ), Ф 1( и + , У 2 + ) ^Ф 1( У 1 + , и + ),

7) У 1 <  и _ , у 2 >  и + ^ решить две одномерные задачи

Ф1( и -, у 2) ^ min, у 2 е [ и _, и+]   ^     у 2

Ф1( У1, и +) ^ min, у1 е [ и _, и + ]   ^     у+,

положить	( min   min )   [( и - , У 2 )»   Ф 1( и - , У 2 ) ^Ф 1( У + , и + )» 1 ’   2        1 ( у + , и + ),    Ф 1 ( и - , у 2 ) >Ф 1 ( у + , и + ),
8) У * >  и + ,	у * <  и - ^ решить две одномерные задачи

Ф1( и +, у 2) ^ min, у 2 е [ и _, и+]   ^     у +

Ф1( у 1, и -) ^ min, у1 е [ и _, и + ]   ^     у-, положить

( У    у 2^min ) =

^{( и} + , у 2 X . ( у - , ^и - X

^Ф 1^{( и} + , у 2 ) ^^Ф 1 ( у - , ^и - X

^Ф 1^{( и} + , у 2 ⁺ ) >^Ф 1⁽ у 1 - , ^и - ).

Представленная процедура обеспечивает точное решение двумерной задачи на минимум без применения итерационных алгоритмов.

• 3    Задача на максимум нормы конечного состояния

Рассмотрим задачу максимизации нормы, которая представляет собой характерный пример невыпуклой оптимизации. После параметризации задача может быть формализована следующим образом:

ф ( у ) ^ max,       у е Y .                      (6)

Здесь

ф ⁽y ) = dd , y ) + ¹ Xyy , Xy\

^Y = ^{ У = ⁽ У i ,-, У т ^): У / ^{e [} u - , u + 1, i = ^{1 m }} .

Предположим, что матрица X e R" ^{x m} имеет максимальный ранг, т. е. ф (у ) — строго выпуклая функция.

Выделим множество угловых точек гиперкуба Y (2 ^т вершин)

Y * = { у e Y : y i = u _v u ₊ , i = 1, m}.

Будем использовать известный результат: если y ⁰ — глобальное решение задачи (6), то y ⁰ e Y * .

Сформулируем задачу на множестве угловых точек

ф ( y ) ^ max,       y e Y * .

Согласно предыдущему утверждению, задачи (6) и (7) эквивалентны.

Решение задачи (7) в простейшем варианте реализуется полным перебором 2 ^т угловых точек и соответствующих значений функции ф . Если эта процедура по вычислительным затратам не допустима, то можно организовать перебор угловых точек с монотонным увеличением значений ф ( y ). Здесь идеально подходит метод условного градиента на множестве Y _* . Проведем описание итерации метода.

Пусть y k e Y * . Тогда

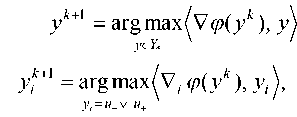
yk+1 = arg max (Vф( yk), y yeY*

yk+1 = argmax(vi ф(yk), yi У i = 1, m.

y i = u _ v u +

о

Таким образом, для i = 1, m

u

u + ,

V ф (y k ) <  0,

V ф(yk) > 0, u_v u+, Vi ф(yk) = 0.

Понятно, что yk+1 e Y*,     ^Ф(yk), yk+1 _yk) > 0.

Если y k ^{+ 1} ^ y k , то имеет место строгое возрастание для функции ф :

ф ( y k ^{+ 1} ) - Ф ( y k ) >^ ф (y k ), y k ^{+ 1} - y k \

Пусть для некоторого индекса i е {1,..., m} V i ф (y^k ) - 0. Тогда у ^ ^{+ 1} - и - v и ₊ , т. е. всегда можно обеспечить условие y^{k + 1} * y^k , что влечет за собой свойство увеличения ф ( y^{k + 1} ) >  ф ( y^k ).

Таким образом, условием остановки итерационного перебора является совпадение y^{k + 1} - y^k , из которого следует, что V i ф (y^k ) * 0, i - 1, m .

Укажем один вариант тестирования точки у на оптимальность в случае остановки метода улучшения: y^{k + 1} - y^k . Проведем перебор соседних с y^k угловых точек y^{k ,} j , j - 1, m на предмет увеличения функции ф по сравнению с ф ( y^k ).

Если такое увеличение произошло, то соответствующая вершина y^{k , j} выбирается в качестве начального приближения для следующего цикла итераций метода условного градиента. В противном случае вершину y^k можно объявить локальным максимумом в задаче (7).

Остается отметить, что соседняя угловая точка y^{k , j} получается из y^k переключением j -той координаты у^к между двумя значениями и _ , и ₊ : если у^к - и - ( и ₊ ), то у^к , ^j - и ₊ ( и - ).

• 4    Иллюстративные задачи

Пример 1. Оптимальное по энергии управление гармоническим осциллятором [3]:

x , - x ₂, x₂ =- x 1 + и , x 1 (0) -- 1, x ₂ (0) - 1;

| и ( t )| <  1, t е [0, п ];

^{Ф ( и} ) = J ^Х 1^{2( п} ) ⁺ x 2 ^{( п )).}

п

Реализуем параметризацию для m - 2, у - ( у 1 , у ₂), t , = —.

В результате простых расчетов получаем

Ф (0) = 1,

X =

:/

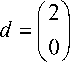
^ф 1^{( у} ) - ^{1 + 2 у} 1 ^{+ у 2 + у 2} .

Переменные у 1 , у ₂ в выражении для Ф 1 ( у ) разделены, т. е. задачи Ф 1 ( у ) ^ ext , | у | < 1 решаются элементарно.

Первая задача Ф1(у) ^ min, | у |< 1 имеет единственное решение ушш - -1, у min - 0, причем Ф1( уmin) - 0. Следовательно, управление u min ( t ) —

- 1, t G [0, ^, 0, t G ( ^П , П ].

является оптимальным в исходной задаче

Ф ( u ) ^ min,     u g V .

Вторая задача Ф1(y) ^ max, | y |< 1 имеет два решения y1max = 1, ymax — ±1, причем Ф1(ymax) — 5. Соответствующие управления umax (t) = 1     t G [0, П],

1, t G [0, -],

11    (f\ — J                 ²

1,

П tG (pn].

Следует отметить, что известно оптимальное управление в задаче Ф(u) ^ max, u g V uopt (t) — *

1,

1,

_г„ 3 п, t G [0, —],

. 3п    л tG (—,п],

со значением Ф ( u_opt ) — 3 + 2_V2 « 5,82 .

Это управление получено в [2; 8] в результате нетривиальной численной реализации на основе условия глобального максимума. Управления u _max ( t ), построенные аналитически, имеют простую структуру и обеспечивают неплохое приближение к оптимуму по значению функционала (отклонение 14%). При этом точное оптимальное управление получается в результате процедуры параметризации для m — 4 перебором 2 ⁴ угловых точек.

Пример 2. Задача на экстремум нормы конечного состояния для двухступенчатой системы x1 — x 2,

x₂ — u ,      x 1 (0) — x f ,      x ₂(0) — x 0 ;

I u ( t )| <  1, t G [0, T ]; Ф ( u ) — 1( x 2 ( T ) + x 22 (T )).

Для приближенного решения задачи Ф ( u ) ^ min с числовыми данными T — 2, х° — 2, x 0 — - 1 применим процедуру параметризации для m — 2.

В этом случае

ф (0) = 2,

X =

( 1     1 j

,

d =

(—1) •V 17

Ф 1 ( у ) = Ф (0) + dd , у ) + 2 X , Xy) .

Стационарная точка параболоида Ф1(у) определяется линейной системой d + XT Ху = 0, которая конкретизируется в виде

13 у 1 + 7 у 2 = 4,    7 у 1 + 5 у 2 = 4

*

с решением у₁ =

—

1      2    3

2, ^{у 2} = 2

.

Точка у 2 =2 нарушает ограничение | у ₂ | <  1, поэтому в соответствии со схемой решения из раздела 2 полагаем у + = 1 и решаем первое уравнение

¹³ у 1 ^{+ 7} у 2 ⁺ = ⁴     ^     у +

—

.

В результате получаем точку минимума ymin

У 2™ = 1.

— 13, которой соответствует управление

/, minx u (t, у ) = I

13,

1,

t G [0, 1], t g (1, 2],

и значение функционала Ф[ ( у ^min ) = —

.

¹           26

Для задачи на максимум нормы ( Ф ( u ) ^ max, u g V ) оптимальное управление известно [8]:

u op_t ( t ) = — 1,       t g [0, 2].

В рамках рассмотренной параметризации оно получается перебором по четырем вершинам квадрата, что приводит к оптимальному результату:

max _ ,,max _ i ^у 1 = ^у 2 =^{— 1} .

Заключение

Задачи на экстремум нормы конечного состояния линейной системы рассматриваются на множестве кусочно-постоянных управлений на заданной сетке узлов аппроксимации. Соответствующая конечномерная задача на минимум является выпуклой и эффективно решается стандартными алгоритмами квадратичного программирования. Специфика невы- пуклой задачи на максимум позволяет получить глобальное решение посредством процедуры конечного перебора явного набора угловых точек допустимого множества.