Коррекция полета тяжелой материальной точки в среде с сопротивлением при наличии геометрических ограничений на дополнительные управления

1. Уравнения движения управляемой точки и требования к кинематике полета

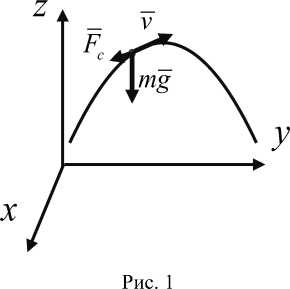
В работе [5] были выведены дифференциальные уравнения управляемого полета тяжелой материальной точки в однородном поле тяжести в среде с сопротивлением, пропорциональным квадрату скорости (см. рис. 1).

Эти уравнения имеют вид mx = - k (x2 + y2 + z1 )*

x

^^= + V , ¹

my = - k ( x ² + y ² + z ² ) *

y

*  /                  + V2, x + y + z mz = - k (x2 + y2 + z2 )*

*

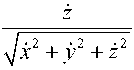
- mg + V 3 ,

или

^k        2     2     2 ¹

x =—x * у x + y + z +— v1, mm

k         2     22

y =--y ’ \x + y + z + mm k  222

z =—z• vx + y + z -g+ mm

(1.1)

где z — вертикальная, x , у — горизонтальные, координаты точки, m — ее масса, g — ускорение силы тяжести, k = const — коэффици-

ент пропорциональности, а

^V 1

v 2

v

— вектор

управляющих параметров. К кинематике полета предъявляются следующие требования. Движение начинается в момент времени t и заканчивается в момент времени T >  t^ на поверхности земли в положении, близком к точке ( x_T , y_T, z_T ) . При этом полет должен происходить на высоте не менее 8 >  0 (за исключением заключительной фазы полета) и не более 2 8 >  0 от поверхности земли. Начальное положение и начальные скорости точки заранее не определены. Про них лишь известно, что они удовлетворяют условиям

Х0 ~ 0, У0 ~ 0, z0 е[^(Х0,У0 ) + 8,^(ХгУ0 ) + 28] , xyz

Хо ~ —  , Уо ~ —  , Zo ~ —

0              ^0

1    t 0          t    10          t1

где p : R ² ^ R ¹ - гладкая функция двух переменных, моделирующая рельеф местности.

Х = Х ( t ) , у = у ( t ) , z = Z ( t ) t е [ 1 0 , T ] . будем называть базовым законом движения, если

^Х ( t 0 ) = ⁰, ^У ( t 0 ) = ⁰,

^Z ( t 0 ) ^е[Н ^Х 0 , У 0 ) ^{+ 8 ,} ^ ( ^Х 0 , У 0 ) ^{+ 2 8} ] ,

^Х ( t 0 ) =         . ^У ( t 0 ) =    ' .

T t 0               T    t 0

и он удовлетворяет всем требованиям, предъявляемым к кинематике полета.

Приведем один способ построения базового закона движения точки. Полагаем

Х = 0, У 0 = 0, Х = \ Х ,У 0 = '   ^ ,

T    t 0             T    t 0

^Х ( t ) = ^Х 0 + ^Х 0 ( ^{t — t} 0 ) ,

^У ( t ) = ^У 0 ^{+ У} 0 ( ^{t — t} 0 ) , t ^е [ t 0 , T ] •

Пусть  tx g( t0, T )  и s — натуральное число.

Разобьем промежуток времени [ t ₀, T ] точками

^T 0 = t 0 , ^T 1 = ^T 0 + ^"^{, T} s = ^T s — 1 ^{+ Д} = T ,

Точные

значения

x o , ^У 0 , z 0 , x 0 , ^y 0 , z 0

начальных условий становятся известными

Д =

±t 0

s

только в момент старта. Управление движением точки будем осуществлять в классе программных стратегий.

Определение 1. Произвольная интегрируемая вектор-функция v : [ t ₀, T ] ^ R³, называется программным управлением точкой на промежутке времени [ 1 ₀ , T ] .

В статье решается следующая задача управления полетом точки.

Задача. Построить программное управление v ⁰: [ t ₀, T ] ^ R³ материальной точкой, которое обеспечивало бы выполнение требований, предъявляемых к кинематике полета.

2. Базовый кинематический закон движения точки и базовое программное управление

Не теряя общности, считаем, что для некоторого номера s_c <  s выполняется равенство т = t . В противном случае разбиение про- s c         ¹

межутка времени [ t0, T ] можно сделать ча стично неравномерным.

Далее нарабатывается массив точек

( ^Т 0 , ^Z 0 ) , ( т , ^Z 1 ) ^’^ ( ^T s , ^Z s ) ,

где

^Z 0 e[ H ^Х ( ^т 0 ) , ^У ( ^т 0 ) ) ^{+ 8} ,

Н Х (т0 ),У (т0)) + 28 ],

^Z 1 е[ р ( ^Х ( т ) , ^У ( ^т 1 ) ) + ⁸ , ^ ( ^Х ( ^т 1 ) , ^У ( ^т 1 ) ) + ^{2 8} ] ,

Введем понятие базового закона движения точки.

Определение 2. Кинематический закон движения точки

Z sc еИ Х ^с ) ’ У К )) + 8’

^(Х (Tsc ) ’ У (.У )) + 28 ’

zs_c + 1

€

T - Tn

^ ( x ( ^T s c + i ) , y ( ^T s c + i ) ) + * • T-y- s_c

T :

^(x (TSc +1 ) , y (TSc +1 )) + 2£ • sc

+ * • T        ,

^T : T s c

^Z s - 1 ^e   ^ ( x ( ^T s - 1 ) , y ( ^T s - 1 ) )

^( x (Ts-1 ) , y (Ts-1 )) + 2* • T^^ , T - TSc J zs = ZT .

Функциональная зависимость

^Z ( t ) = f ( t ) , t ^€ [ t 0 , ^T ]

устанавливается путем интерполяции массива точек. В результате получим n f (t ) = ! ait.

i = 0

Выбирая число промежутков s достаточно большим, а степень интерполяционного полинома достаточно высокой, можно добиться того, что кинематический закон движения точки x = -X (t), y = y (t), z = Z (t), t e[to, T]                 (2.2)

будет базовым.

Определение 3. Программное управление v = v(t),   t e[to,T], реализующее базовый закон движения точки, назовем базовым программным управлением.

Для построения базового программного управления уравнения (1.1) разрешаем относительно управлений:

v = mx + kx • ^x1 + y2 + Z2, v2 = my + ky • ^x2 + y2 + Z2,       (2.2)

v ₃ = mZ + kZ • x ² + y ² + Z ² + mg .

Базовый закон движения (2.1) подставим в уравнения (2.2). В результате получаем искомые базовые управления

vt (t) = mx (t) +

+kx (t) • 7x2 (t)+y2 (t)+z 2 (t),V2 ( t ) = my ( t ) ++ky (t) • 7x 2 (t) + y 2 (t) + Z 2 (t),

V3 (t) = mZ (t) +

+ kZ ( t ) • x ² ( t ) + y ² ( t ) + Z ² ( t ) + mg .

• 3.    Возмущенные начальные условия и возмущенные движения

Пусть

	7 X x voz 0 y voz 0		=	Z - \ x 0 y ˆ 0	+	[ S x 0 1 ^ y 0	,	[ S x 0 1 S y 0	* 0,
	V z voz 0 7			V z 0 7		V s z 0 7		V s z 0 7
x voz 0				x ( t 0 )	11	r S x 0	1	r S x 0	1
	• y voz 0	=	= y ( t 0 )		) + S y 0		’	S y 0	* 0
	z voz 0 7		V'	z ( t 0 )	• 7	V s z 0 7		3z V S Z 0 7

где величины

r Sx₀

^S y 0

V u o 7

^ ^x o ^S y 0 Sz

V ^uz 0 7

малы .

Определение 4. Вектора vo 0

y

V ^Z voZ 0 7

(x A xvoz 0

^{y o 0}

V ^Zvoz 0 7

назовем возмущенными начальными условия- ми, а вектора

Г S x ₀ ^Л

S y⁰

V ^S z 0 7

* 0,

r S x 0

S y 0 * ^{0 -} возму-

V S Z 0 7

щением начальных условий точки.

Обозначим x = xvoz (t ) , y = yvo. (t ) , Z = ZVOZ (t ) , t e[10,T]                 (3.1)

– решение системы дифференциальных уравнений k        2     2     21

x =--x • yx + y + Z +— Vj (t), mm

y = - Zy • 7 x2+y2+z2 +—v2 (t), mm

z = - —= • 7 x2+y2+z2 - g+7 V3 (t), mm с начальными условиями x (t0 ) = xvoz 0 , y ( t0 ) = yvoz 0, Z ( t0 ) = zvoz 0 , x (t0 ) = xvoz 0 , y ( t0 ) = yvoz 0 , Z ( t0 ) = zvoz 0 .

Определение 5. Кинематический закон движения точки (3.1) назовем возмущенным движением, а разность

r t x ( t )Л		Г x voz ( t ) '		Г x ( t )!
t y ( t )	=	У voz ( t )		y ( t ) ,
l t z ( ' ) ,		l z voz ( t		i z ( t J
г t x ( t )4		Г x voz ( t )'		' x ( t )1
t y ( t )	=	У voz ( t )	—	y ( t ) .
i t z ( t ) >		z ˆ t l voz у у)		z ( t ) l)

t ^ [ t 0 , T ]

возмущением движения точки.

4. Минимизация возмущений

Основная идея решения задачи управления точкой, сформулированной в первом пункте, состоит в построении управления, вынуждающего точку двигаться по кинематическому закону, который, начиная с момента времени t₁ g [ t ₀, T ] , мало отличается от базо

вого закона движения. Для этого требуется обнулить возмущения в момент времени t i< t о , T ] .

Обнуление возмущений будем осу-

ществлять при помощи дополнительного

управления

u (•)=

г u m u2 (0 lu3 0j

которое вводится в дифференциальные уравнения (1.1) аддитивно основному управле-

	Г 0	0	0	1	0	0 ^
	0	0	0	0	1	0
	0	0	0	0	0		1
	a 0	a 0	0	d F	d F	В
A ( t ) =				d x	3 y	a z
	0	0	A 0	d F	d F2	d F
				d x	d y	d z
	0 l	0	0	d F d x	.   d F 3 d y	.    d F 3 d z )		x = x ( t ) , y = y' ( t ) z = z ( t ) , v i = v i ( t ) , i = 1,2,3
		Г 0	0	0 Л		Г q 1'
		0	0	0		q 2
B ( t ) =		0 1 m	0 0	0 0	, q =	q 3 q 4	G j	6 ,
		0	1 m	0		q 5
		l 0	0	1 m ) k --. m		l q 6 >
F 1 ( x . y . z . v 1			) =		x • yjx2	• 2     -2 + y + z +
1 +- v 1 . m				k — m
F 2 ( x . y . Z . v 2			) =		y • ylx 2 + y		2 +	z 2 +
1 + — v 2 , m				k — m
F 3 ( x, y, z, v 3			) =		z • V x2	• 2     -2 + y + z —
— g +	1 v m	3 .

нию, т. е.

x = —— x • x2 + y2 + z2 + —(v (t) + u ), mm

y = - — y • 7x2 + y2 + z2 + — ( v2 (t) + u 2), mm

z = — — z • Jx2 + y2 + z2 - g + — (v3 (t) + u3). mm

Динамика управления возмущениями приближенно описывается векторным линейным дифференциальным уравнением [5]:

x = A ( t ) q + B ( t ) u ,           (4.1)

где

При отсутствии геометрических ограничений на дополнительное управление для начального возмущения

Г tx0' ^y0 q (t0 ) = 0 tx0 ty 0 ltz 0 ) в работах [5-6] задача обнуления фазового вектора линейного объекта (4.1) в момент времени ( g[ t0, T ] была решена.

При этом разрешающее управление в работе [5] было оптимально по критерию "минимум энергии", а в работе [6] – по критерию "минимум силы". Терминология взята из монографии [1].

В данной статье принимается, что u g P , где P о R ³ — выпуклое компактное множество. Символом П_р [ t ₀, t j ] обозначим множество всех программных управлений на промежутке времени [ t ₀, t_{ ] , для которых выполнено включение u ( t ) g P , t g [ t ₀, t_x ] . В силу геометрических ограничений на управление u ( • ) задача обнуления фазового вектора системы (4.1) в момент времени ( g [ t ₀, T ] может и не иметь решения. Вместо нее здесь решается задача минимизации расстояния от фазового вектора в момент времени t до

Теорема 2. Пусть ^{s (} t 0 , ^q 0 ) > ⁰ и u ⁰ ( • ) g П_р [ t ₀, t_x ] — программное управление, для которого выполнено условие

||^{q (} t i , t 0 , ^q 0 , ^u ( •^{) )}|| = ^{s (} t 0 , ^q 0 ) > ⁰ .

Тогда

HH [ t ] u ° ( t ) , l °^ = min H l [ t ] u , l °^, t ^g[ t 0 , t i ] .

Изложим алгоритм построения программного управления u ⁰ ( • ) g П^ [ t ₀, t_x ] , решающего задачу минимизации расстояния от фазового вектора линейного объекта до начала координат в случае, когда s ° ( t ₀, q ₀) >  0 и

|u | <  a , | u ₂| <  a ₂, | u ₃| <  a₃ > .

начала координат.

Указанное минимальное расстояние s ⁰ ( t ₀, q ₀) вычисляется по формуле [2]

1. Вычисляется величина

^s ( t о , q 0 ) = max { ⁰,  max [( Q [ t i , t о ] * o , 0 ] ,

t ₁

+| min H [t] u, tydt t0

\ ,        (4.2)

(H [ t ] u , l) =

' h i ( t ) h i ⁽ t )

4 ^h 6i ⁽ t )

^hi2 ( t )

hi2 ( t )

^h 62 ( t )

h i3 ( t ) 1

h3 (t)

^ u _i ^Л

u v u 3 >

h63 ( t ) ;

где  Q [ t, t ], t , t g[ tQ, tx ] —  фундаментальная матрица Коши для однородного уравнения q = A (t) q , а H [ t ] = Q [ ti, t ] B (t), t ,t g[ to, ti ] — матрица перехода для линейного объекта (4.1). Заметим, что если S (t0, q0) > 0 , то обнулить возмущения в момент времени t нельзя в принципе.

Алгоритм решения задачи минимизации основывается на следующих двух утверждениях [1–2].

Теорема 1 . Пусть S ( t ₀, q ₀ ) > 0 .

Тогда максимум в (4.2) существует и достигается на единственном векторе l⁰ g R ⁶,|| l ⁰|| = 1 .

Символом q ( • , 1 ₀, q ₀, u ( • ) ) обозначим движение линейного объекта (4.1), выходящее из начального положения ( t ₀, q ₀) и порожденное управлением u ( • ) g П_р [ t ₀, t_x ] .

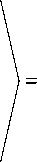
(Л

X Mt) uj j=i

,

E M t )( t ) u , ^V l ■ ^У

Ij=i

(^ =E E j t) uj li = i=i V J =i

= E|Eh,(t)li uj =XJt,l)uj, j =i V i=i            У где

^ j ( t , l ) = E j t ) l i ,  j = i,2,3.

i = i

2. Решается задача математического программирования

4. Строится оптимальное управление

<

( H [ т ] u . 0 = Z a ( t , l )

j = 1

u ⁰

u e P.

' U 1 ⁰ ( t , l ⁰ f

(t ) = U0 (t, l0 )=  U20 (t, l0)  , кU 0 (',10), t e [t0, t1 ]

(4.3)

Пусть U ⁰ ( t , l ) = U 0 ( t , l ) - решение

U ⁰

ется

этой задачи. Тогда

5. Производится проверка. Интегриру-дифференциальное уравнение

dq (t ) = A (t) q (t) + B (t) u0 (t), t e[ t 0, t1 ]

- a

U j ( t , l ) = j ve[- a j , a j. ] ,

^a j^,

a j ( t , l ) = 0, ^ ( t , l ) <  0.

с начальными условиями q ( t ₀ ) = q ₀. Обозначим q ⁰ ( • ) = q ( • , t ₀, q ₀, u ⁰ ( • )) . Должно выпол-

няться

- a j • sign [ o j ( t, l ) ] ,

j = 1,2,3 .

e ( t 0 , « 0 h p ( q ⁰ ( t ) , { 0 })=| q ° ( t ,)| .

4. Вычисляется величина

j = 1

5. Решение основной задачи управления

Полагаем

—

j = 1

3. Решается задача математического программирования

t 1

<

t ₀

^t 1     3

( Q ^[ t 1 , t 0 ^] q 0 , ^l ) ^- |Z ^a j |^a j ^{( т} , ^l ) I d

1 0 ^j = 1

Z lf = 1.

i = 1

l ₁

f v1 (' )1 V (t) кV(t )J f к t)+u0 (t )1 V2 ( t ) + u0 ( t ) кv (t) + u0 (t)? f v (t n ' ( t ) , кv3 (t);

t ^{e [} t 0 , t 1 ^]

t e ( < 1 - T ]

(5.1)

Пусть l ⁰ =

l i ⁰

1 ⁰ к ¹ 6

Заметим, что e0 (t.,

- ее решение.

+J H [т] U0 (т, l"), l0 T = t0

^t 1     3

т .

t 0 ^{j 1}

Обозначим xkor ( t ) , У—ог ( t ) , zkor ( t ) , t e[ t0, T ]- решение системы дифференциальных уравнений x = - — x •  x2 + y2 + z2 + — v 0 (t), mm y = -—y • 7 x2+y2+z2 +—V0 (t ), mm z = -—z • 7x2 + y2 + z2 - g + — V0 (t), mm с начальными условиями x (t0 ) = xvoz 0 , y ( t0 ) = yvoz 0 , z ( t0 ) = zvoz 0 , x (t0 ) = xvoz 0 , y ( t0 ) = yvoz 0 , z ( t0 ) = zvoz 0 •

Определение 6. Закон движения xkor (•) , Уког (•) , zkor (•) называется откоррек- тированным законом движения точки.

Откорректированный закон движения динамического объекта приближается к базо- вому закону движения в момент времени tx g[t0, T] на расстояние г° (t0, q0). В случае, когда эта величина мала, дальнейший полет точки будет происходить в малой окрестности базового закона движения. Таким образом, требования к кинематике полета будут вы-

Г V 0 ^ v 0 ( • )

I v 0 C) J

полнены, и управление

будет решени-

ем задачи, поставленной в пункте 1.

6. Численный эксперимент

Изложенная выше теория иллюстрируется на следующих числовых данных:

k = 0.45, m = 100 кг , g = 9.8 м , г = 30 м , сек ²

t ₀ = 0, T = 10 сек , p ( x , y ) =50 • sin ( 0.00005 • x • y ) м , x ₀ = - 40 м , y ₀ = 20 м , z ₀ = 40 м , , x_T = 3000 м , y_T = 100 м , z_T = ф ( x_T , y_T ) = 32.51 м , мм  м

X0   310     ,y0     10     , z0   —12.75     , cек          cек            cек s = 100, t* = 5 сек ^ sc = 50, n = 15, a = 2050 н, a2 = 2050 н, a3 = 2050 н .

Здесь г0 (t0,p0 ) = 0.38 м > 0 и, следовательно, задача обнуления возмущений не разрешима. Этот факт подтверждается и путем вычисления величин u^=maxu0^ t), t G[ t 0, t1 J u0 . = max u0 -tt )|, i = 1,2,3, сил1      t g[ 10, t1 J сил где u0 (•), uL (•)- оптимальные управления, решающие задачу обнуления возмущений, полученные в работах [5], [6] соответственно. Имеют место неравенства u э. = 2293,7 н > 2050 н, энер uc^ = 2172,1 н > 2050 н (i = 1, j = 1), которые означают нарушение геометрических ограничений u g P для управлений uU (•),ul (•).

На рис. 2–4 приведены покомпонентные графики управления u ⁰ ( • ) , вычисленного по формулам (4.3). На них мелким пунктиром нарисован график компоненты управления, а крупным – граница области ее изменения.

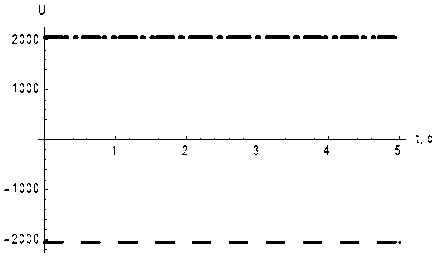
Рис. 2. Первая компонента управления

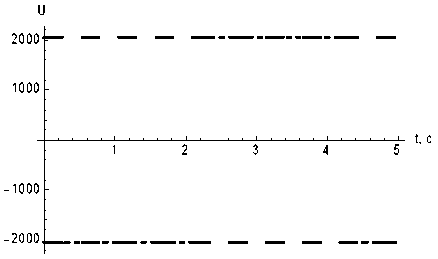
Рис. 3. Вторая компонента управления

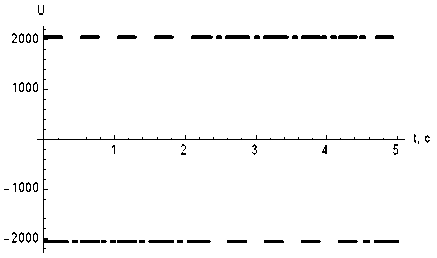
Рис. 4. Третья компонента управления

Таким образом, управление u ⁰ ( • ) удовлетворяет включению u ⁰ ( t ) g P , t g [ t₀ , t_x J и представляет собой кусочно-постоянную функцию, принимающую значения на границе своей области изменения. Непосредственно убеждаемся, что

II p ( t 1 , t 0 , p 0 , ^{u 0} ( • ))] = 0.4 ^м ~

« 0.38 м = г ⁰ ( 1 ₀, p ₀ ) .

Следовательно, управление и ⁰( • ) действительно решает задачу минимизации расстояния от фазового вектора линейного объекта в момент времени t = 5 сек до начала координат. Величина s ⁰ ( t₀ , p ₀ ) = 0.38м мала по отношению к величине дальности полета, поэтому управление, решающее задачу для исходного нелинейного объекта, можно построить по формуле (5.1).

На рис 5. приведены совместные графики координаты z = z_kor ( t ) , t e [ t o , T ] точки в движении по откорректированной траектории (тонкая линия) и рельефа местности z = ^ ( x kor ( t ) , Укок ( t ) ) , t ^e[ t 0 , T ] (жирная ^линия).

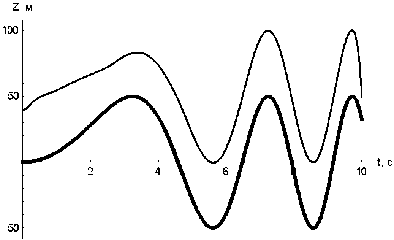
Рис. 5

Из рисунка видно, что для откорректированного движения фазовые ограничения на полет точки выполнены. Заметим, что промах по цели в конечный момент времени для откорректированной траектории составляет величину 2.02 м .

На рис. 6 показаны трехмерные траектории точки в базовом (штриховая линяя) полете и откорректированном (сплошная линия) полете.

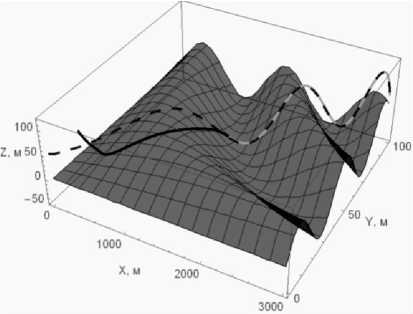
Рис 6

Из рисунка видно, что в момент времени t = 5 сек откорректированное движение почти выходит на базовое движение и в дальнейшем с ним практически совпадает.

Заключение

• 1.    В статье ставится и решается задача управления полетом тяжелой материальной точки в среде с сопротивлением, пропорциональным квадрату скорости в условиях неполной информации об ее начальном положении. Эта информация становится полной только в момент старта.

• 2.    Решение поставленной задачи осуществлено путем сближения возмущенного движения точки с базовым законом ее полета.

• 3.    Указанное сближение реализовано в условиях геометрических ограничений на дополнительные управления.

• 4.    В численном эксперименте показана эффективность применяемых алгоритмов управления.