Корректировка рыночной стоимости по ценообразующему фактору "площадь объекта"

4 База ГУП «ГУИОН» доступна для членов саморегулируемой организации оценщиков «Сообщество профессионалов оценки» на официальном сайте организации

цена, тыс. р./кв. м

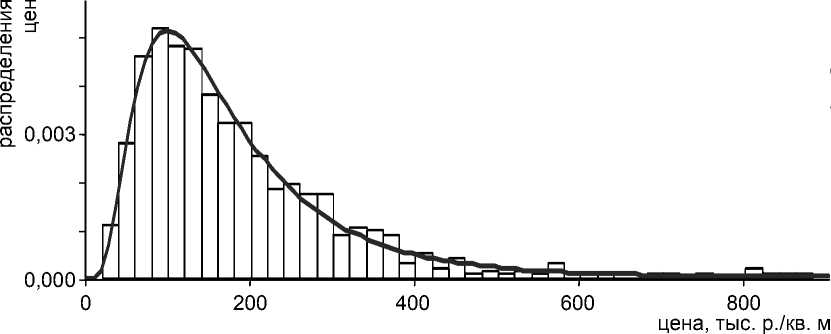
а)

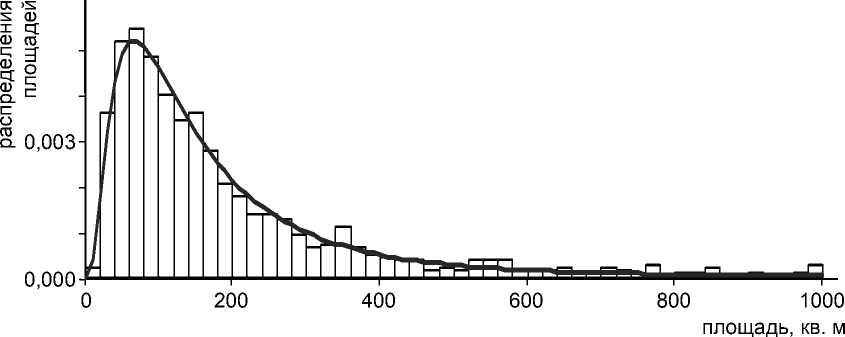
б)

Рис. 1. Эмпирические распределения цен предложений (а) и площадей (б) торговой недвижимости и их аппроксимация логарифмически нормальным распределением

Ж1

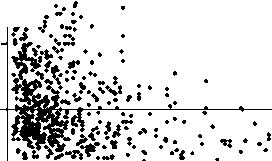
площ адь, кв. м

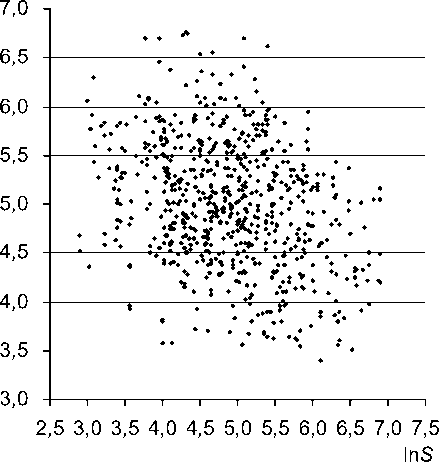
• а)                                                 б)

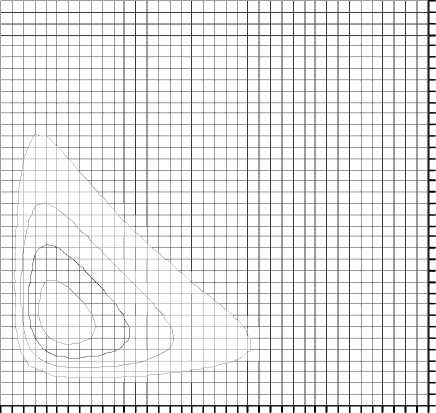
Рис. 2. Выборка по торговой недвижимости в плоскости S , V (цена предложения – площадь объекта) (a) и в плоскости ln S , ln V (б)

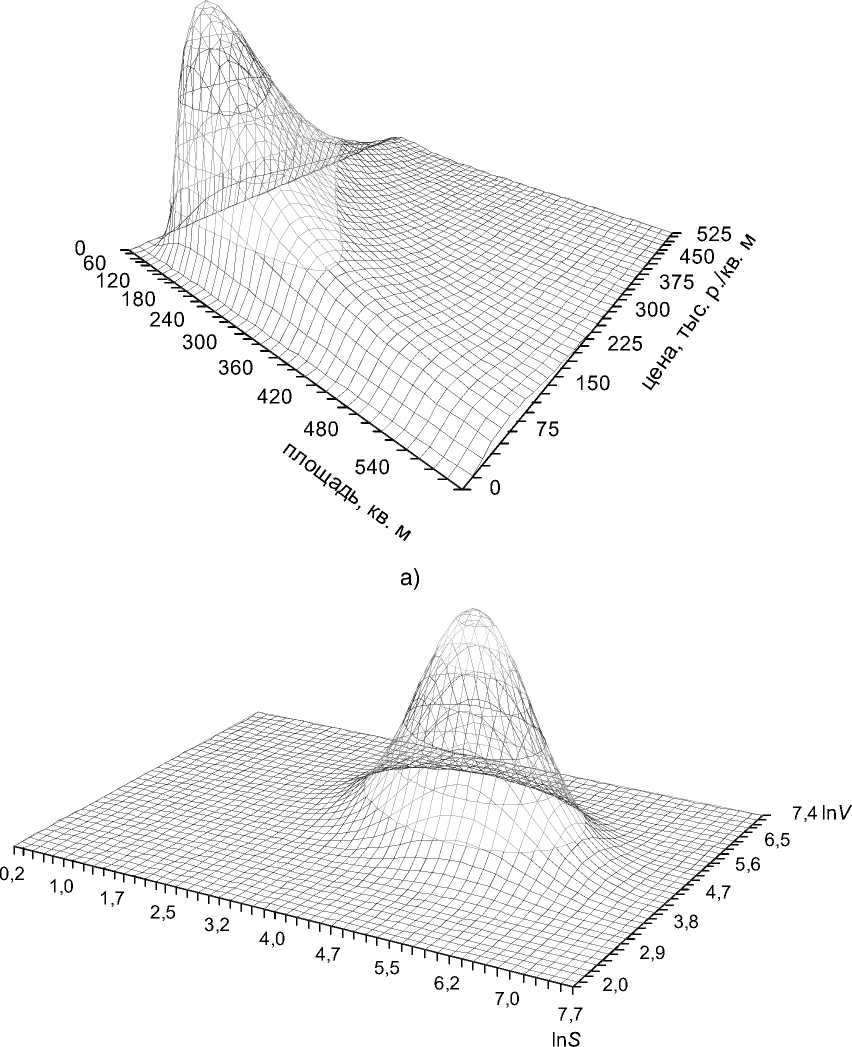
На рисунках 3 и 4 показаны аппроксимация наблюденной двумерной выборки совместным логарифмически нормальным распределением с указанными параметрами (а) и соответствующее нормальное распределение величин ln S и ln V (б).

оооооооооо (DCNOO^OCDCNOO^ ^^СМСОСО^^Ю площ адь, кв. м

540 5 cd

480 ^ Q_

420 У

360 (D

а)

7,4 >

6,8

6,2

5,6

5,0

4,4

3,8

3,2

2,6

2,0

СМСОчГОСОСМСОчГОСОСМСОчГ о О ^ CM CM CO CO ^ in in CD l< ln S

б)

Рис. 3. Аппроксимация выборки логарифмически нормальным распределением. Проекции поверхности плотности совместного логарифмически нормального распределения на плоскость S , V (а) и совместного нормального распределения на плоскость ln S , ln V (б)

• б)

Рис. 4. Аппроксимация выборки логарифмически нормальным распределением. Поверхность плотности совместного логарифмически нормального распределения S , V (а) и поверхность совместного нормального распределения ln S , ln V (б)

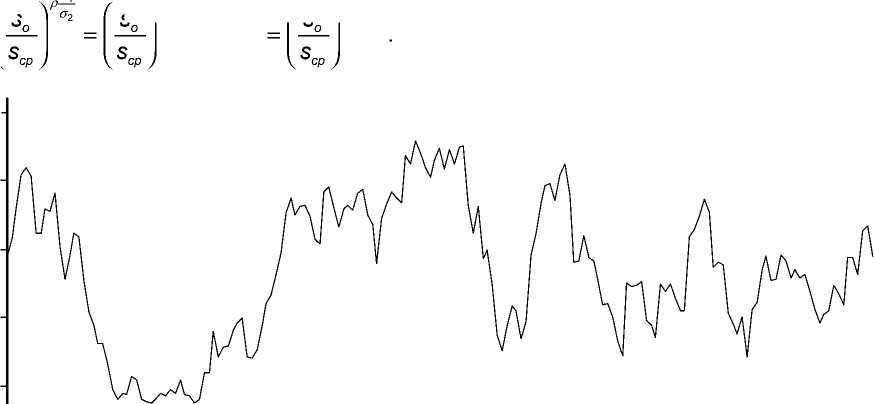
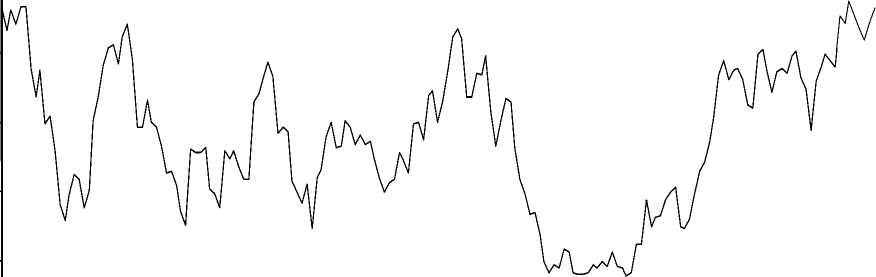
Наблюдаемое визуальное соответствие выборки и аппроксимации следует проверить статистическим тестом. Для этого мы применили «круговой» (см. утверждение 2) КС-тест. Результаты тестирования показаны на диаграмме (рис. 5).

Как для V , так и для S значение p-value больше критического уровня в 5 процентов для любого угла поворота. Принимается гипотеза о совместном логарифмически нормальном распределении V и S .

Поскольку получено статистическое доказательство совместного логарифмически нормального распределения величин V и S , корректирующий коэффициент (4) равен:

ф

Ф

- 0 , 243

0 , 8235

⎛ s

⎛ s

- 0 , 3122 × ^{0 , 6415}

1         0 8235

K =

1,0

0,8

0,6

0,4

0,2

CI ф ф о. ф

s

0,0

угол поворота, градусы

со

1,0

о

ф

ф о. ф

CI ф

а)

0,8

0,6

0,4

0,2

0,0

угол поворота, градусы

б)

Рис. 5. Результаты «кругового» КС-теста для цен V (а) и для площадей S (б) торговой недвижимости (пунктиром обозначено критическое значение p-value , равное 5 процентам)

Корректировка

Начальное распределение цен в выборке логарифмически нормально с параметрами μ ₁ = 5,0095, σ ₁ = 0,6415, характеристика КС-теста хорошая ( p-value = 0,9308 – больше критического уровня в 5 процентов). Наиболее вероятная цена 1 квадратного метра до корректировки на площадь равна:

exp ( μ ₁ – σ ₁ ² ) = exp (5,0095 – 0,6415²) = 99,283 тыс. р. / кв. м

Пусть площадь объекта оценки равна 100 квадратным метрам. Корректируем всю выборку посредством умножения цены предложения за 1 квадратный метр на коэффициент К :

К = (100/sср)-0,243, где sср – площадь соответствующего объекта сравнения.

На рисунках 6 и 7 показаны распределения нескорректированных и скорректированных цен.

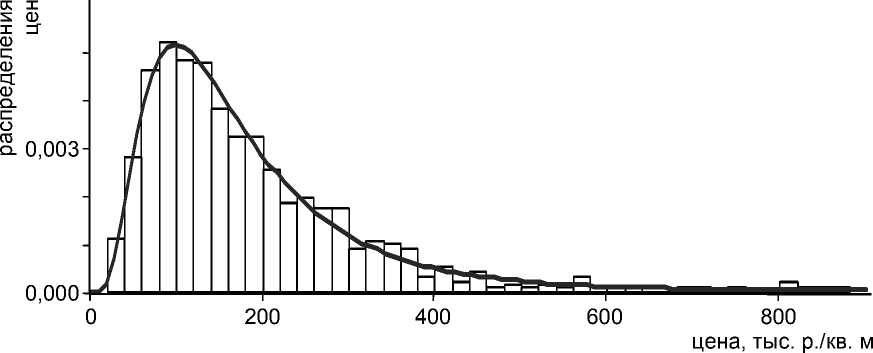
а)

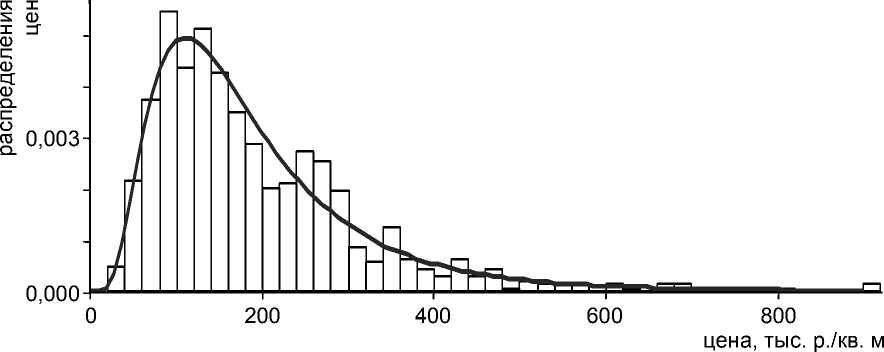
б)

Рис. 6. Распределение цен предложений торговой недвижимости до (а) и после (б) корректировки для объекта оценки площадью 100 квадратных метров

Новая выборка имеет следующие параметры:

^ + р^{0 1} (in s - ^ = 5 , 0095 - 0 , 3122 х 0 , 64 ¹⁵ х (in100 - 4 , 8771 = 5 , 076; o ₂   o "                    0 , 8235

^0 2 ( 1 - р ² ) = ^ 0 , 6415 2 [ l - ( - 0 , 3122 ) 2 ] = 0 , 6094.

Также она имеет и хорошую характеристику КС-теста на соответствие логарифмически нормальному закону распределения ( p-value = 0,4022 – больше критического уровня в 5 процентов). Наиболее вероятная цена 1 квадратного метра (оценка рыночной стоимости) после корректировки на площадь равна:

exp ( μ ₁ – σ ₁ ² ) = exp (5,076 – 0,6094²) = 110,457 тыс. р. / кв. м

Оценка рыночной стоимости 1 квадратного метра увеличилась, так как 100 квадратных метров меньше граничного значения (см. раздел «Граничное значение площади»):

s_o = exp ( μ ₂ – ρσ ₁ σ ₂) = exp [4,8771 – (-0,3122) × 0,6415 × 0,8235] = 154,78 кв. м

Как уже было сказано, при площади объекта оценки менее 154,78 квадратного метра оценка рыночной стоимости 1 квадратного метра после корректировки увеличится, при площади 154,78 квадратного метра оценка после корректировки не изменится, при площади более 154,78 квадратного метра оценка после корректировки уменьшится.

Например, пусть площадь объекта оценки составляет 200 квадратных метров. Корректируем всю выборку посредством умножения цены предложения за 1 квадратный метр на коэффициент К :

К = (200/sср)-0,243, где sср – площадь соответствующего объекта сравнения.

Параметры новой выборки:

+ p^ 1( ln s - ^ ) = 5 , 0095 - 0 , 3122 x 0 , 64 ¹ 5 x (ln200 - 4 , 8771 = 4 , 907.

' о2    o ‘ "                       0 , 8235

Стандартное отклонение прежнее - До^ ( 1 - р ² ) = 0 , 6094 , результат КС-теста хороший ( p-value = 0,4022 – больше критического уровня в 5 процентов). Наиболее вероятная цена 1 квадратного метра (оценка рыночной стоимости) после корректировки на площадь exp ( μ ₁ – σ ₁ ² ) = exp (4,907 – 0,6094²) = 93,282 тыс. р. / кв. м . Оценка рыночной стоимости 1 квадратного метра уменьшилась, так как 200 квадратных метров больше граничного значения s_o = exp ( μ ₂ – ρσ ₁ σ ₂) = 154,78 кв. м .

Если на горизонтальной оси отложить площадь объекта, а на вертикальной оси наиболее вероятную цену (оценку рыночной стоимости), определенную по формуле (1), то для изучаемой выборки (для имеющихся площадей объектов сравнения) получим диаграмму, изображенную на рис. 8 и очевидную, полученную средствами Excel, линию тренда ( x = s ).

Заметим, что, подставляя в формулу (1) полученные ранее значения параметров μ ₁ = 5,0095; σ ₁ = 0,6415; μ ₂ = 4,8771; s₂ = 0,8235; ρ = -0,3122, мы получим не что иное как Mode ( V | S = s ) = 338,32 × s ^-0,243.

Из этого следует, что оценку рыночной стоимости 1 квадратного метра по скорректированной выборке можно получить сразу по формуле условного распределения (1), не корректируя цены выборки. Корректировка выборки посредством умножения цен за

1 квадратный метр на K =

нужна только для последующих последовательных кор- ректировок, так как каждая корректировка применяется к предыдущему результату.

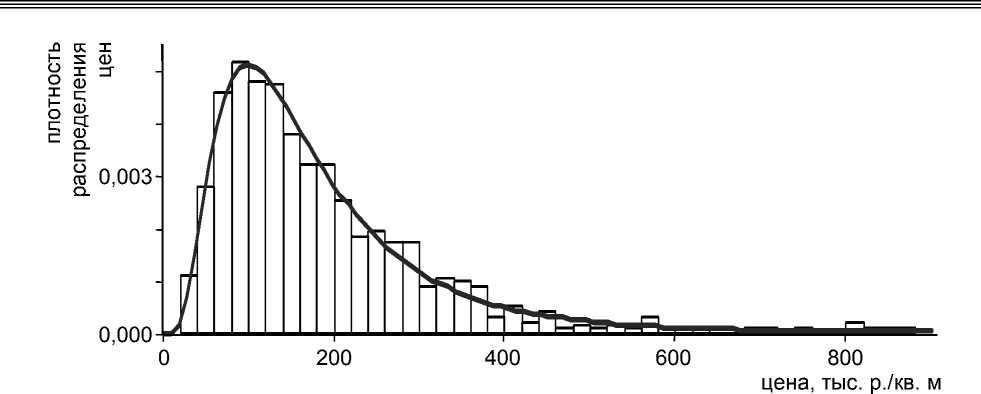
а)

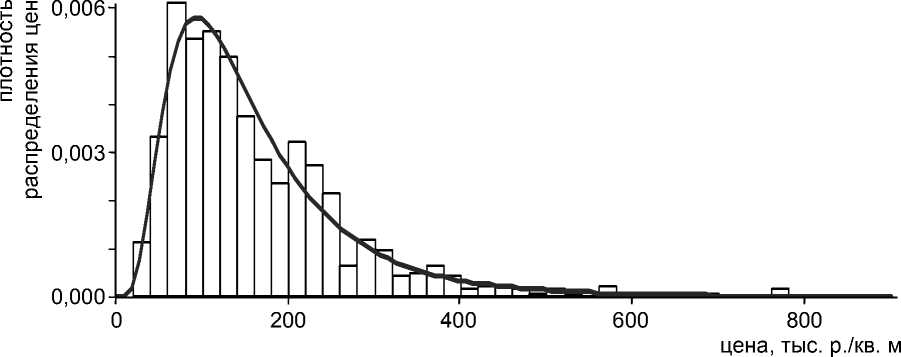
б)

Рис. 7. Распределение цен предложений торговой недвижимости до (а) и после (б) корректировки для объекта оценки площадью 200 квадратных метров

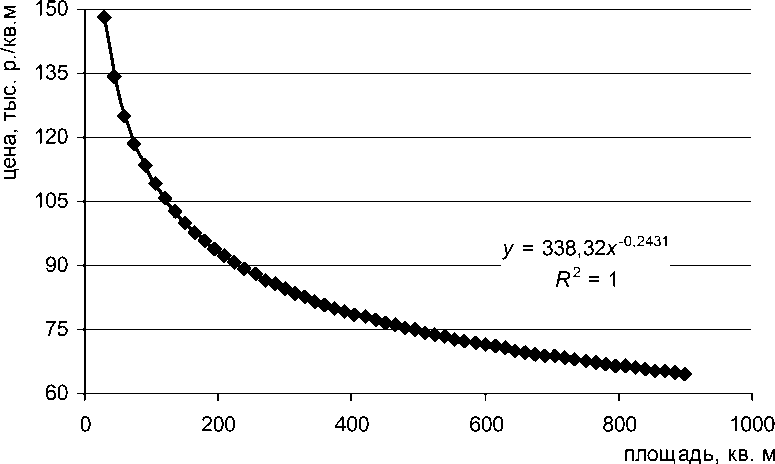
Рис. 8. Зависимость наиболее вероятной цены предложения за 1 квадратный метр от площади объекта

Выводы

При условии совместного логарифмически нормального распределения пары «площадь объекта – цена 1 квадратного метра»:

• 1)    эффект торможения на площадь описывается степенно ́ й функцией;

• 2)    оценка рыночной стоимости может быть найдена сразу по формуле условного распределения (1), так как изучение совместного распределения – это и есть изучение корректировок;

• 3)    корректировка всей выборки проводится для дальнейшей коррекции по другим ценообразующим факторам;

• 4)    в зависимости от площади объекта оценки скорректированная оценка рыночной стоимости может как уменьшаться, так и увеличиваться при одной и той же базе объектов сравнения;

• 5)    при работе с большими базами данных корректировка всей базы полностью соответствует требованиям ФСО № 7.

Приложение

Доказательство утверждения 1

Рассмотрим двумерное логнормальное распределение величин V и S и двумерное нормальное распределение величин ln V и ln S .

Известно, что плотность двумерного нормального распределения с нулевым вектором средних задается при x , y ∈ R следующим выражением:

f_X,Y ( x,y ) =

× exp

2 πσ _x σ _y 1 - ρ ²

1 ⎛ x ² 2 ( 1 - ρ ² ) ^⎜ ⎝ σ x ²

- 2 ρ xy σ _x σ _y

_y 2 ⎞

2 ⎟

где σ _x ² , σ _y ² – дисперсии случайных величин X и Y ;

ρ – коэффициент корреляции компонент вектора X и Y .

Общая формула для условной плотности вектора, имеющего совместную плотность p ( x , y ):

p ( x,y ) p ( y ) ^.

p X|Y = y ( x ) = p ( x|y ) = _+∞ ^{p ( x,y )}

∫ p ( x,y ) dx

-∞

Тогда выражение для формулы условной плотности двумерного нормального вектора f ( X | y ) будет следующим:

f ( X|y ) =                × exp

2 π × σ _x 1 - ρ ²

1 ⎛ xy ⎞

- ρ 2 ( 1 - ρ ² ) ^⎜ ⎝ σ x σ y ^⎟ ⎠

Таким образом, при каждом y случайная величина X имеет нормальное распределение с параметрами E(X|Y=y)=ρσx y, D(X | Y = y) = σx2 (1 – ρ2). Полагая, что X = lnS – μ , σy                                                        2

Y = lnV – μ1, σ12=σy2, σ22=σx2, получаем формулу условной плотности величины lnV при условии lnS = lns:

f ( ln V| ln S = ln s ) =

exp

2 π × σ ₁ 1 - ρ ²

1     _× ⎛ ln V - μ _{1 -} ln s - μ ₂ ⎞ ²

2 ( 1 - ρ ² ) ^×⎜ ⎝ ^σ 1 ^{- ρ   σ} 2 ^⎟ ⎠

Таким образом, условное распределение ln V (при условии ln S = ln s ) нормально с параметрами:

E ( ln V| ln S = ln s ) = μ ₁ + ρ ^{σ 1} ( ln s - μ ₂ ) ; σ 2

D (ln V | ln S = ln s ) = σ 1² (1 – ρ ²).

Следовательно, V распределено логарифмически нормально с теми же параметрами и мода V (наиболее вероятное значение – рыночная стоимость при заданном значении площади объекта) равна:

Mode ( V | S = s ) = exp

μ ₁ + ρ ^{σ 1} ( ln s - μ ₂ ) - σ ₁ ² ( 1 - ρ ² ) ⎥ .

^σ 2                      ⎦

Утверждение 1 доказано.

Доказательство утверждения 2

Для доказательства воспользуемся известным критерием совокупной нормальности – случайный вектор совокупно нормален тогда и только тогда, когда любая его линейная комбинация имеет одномерное нормальное распределение.

Доказательство необходимости

Поскольку поворот – линейное преобразование, а суперпозиция линейных преобразований – также линейное преобразование, любая линейная комбинация компонент вектора ( X _φ , Y _φ ) ^T есть линейная комбинация вектора ( X , Y ) ^T .

Доказательство достаточности

Теперь допустим, что для любого φ ∈ [0,+ π ) каждая из компонент вектора ( X _φ , Y _φ ) ^T имеет одномерное нормальное распределение (с нулевым средним). В частности, Y _φ = X sin φ + Y cos φ . Очевидно, вырожденные случаи sin φ = 0, cos φ = 0 дают одномерную нормальность каждой из компонент X и Y . Рассмотрим невырожденный случай sin φ ≠ 0, cos φ ≠ 0. Запишем (1 / cos φ ) Y _φ = X tg φ + Y , откуда следует, что любая линейная комбинация X и Y c невырожденными коэффициентами является нормально распределенной случайной величиной. Аналогично для X _φ .

Утверждение 2 доказано.