Космологическая модель вселенной, заполненной идеальной жидкостью с нелинейным неоднородным уравнением состояния

Открытие в 1998 г. ускорения расширения Вселенной побудило физиков ввести материальный объект, ответственный за это явление – тёмную энергию. До сих пор неясна физическая сущность данной субстанции, однако феноменологическое моделирование её поведения и влияния на процессы во Вселенной представляет самостоятельный интерес. Одним из вариантов такого моделирования является введение идеальной жидкости с отрицательным давлением.

Расчёт и рассмотрение эволюции космологических параметров

За физическую основу расчётов автором была взята общая теория относительности Эйнштейна (далее – ОТО), метрика – изотропная и пространственно плоская, что неплохо согласуется с наблюдательными данными. Метрики с ненулевой пространственной кривизной представляют самостоятельный интерес как с физической, так и с математической стороны и в данной статье не рас-

сматриваются. Тёмная энергия моделируется идеальной жидкостью с уравнением состояния, введённым I. Brevic и другими авторами [1]:

p = w ( t ) • р + f ( р) + Л .        (1)

Решения с плоской метрикой при линейной и синусоидальной зависимостях w(t) исследованы рядом авторов в работах [2, 3]. В данной работе рассмотрен случай моделирования коэффициента при плотности квадратичной функцией и получена физическая интерпретация результатов.

Решение Фридмана одного из уравнений Эйнштейна без космологического члена имеет следующий вид:

р = 3H2/k2.(2)

Здесь H – постоянная Хаббла, k ² =8πG, скорость света принята за единицу.

Согласно закону сохранения энергии dp/dt+3H(p+p)=0.(3)

Квадратичный коэффициент в уравнении состояния с произвольными пока параметрами a, b, c:

w=3at2 + 2bt + c .(4)

Для сравнения с работами [2, 3] рассмотрим уравнение состояния (1) с нулевым значением лямбда. В этом случае уравнения (1)–(4) дают для плотности следующее дифференциальное уравнение:

dp / dt + 3kkp 3/2(1 + w (t)) = 0.(5)

Его решение даётся формулой p = 4/(3k2[j (1+w(t))dt]2).(6)

Выражение для параметра Хаббла:

H = 2 /(3k2 [ j (1 + w(t))dt]2) .(7)

Ясно, что возможны три разных случая; они в соответствии с формулами Кардано и обозначениями p=(3ac-b2)/3a2,(8)

q=(2b3 -9abc+27a2d)/27a3,(9)

Q=(p/3)3+(q/2)2

задают разный вид эволюции космологических параметров.

Если Q < 0, то кубический трёхчлен в знаменателях выражений (6)–(7) имеет три различных корня, а масштабный фактор даётся выражением r = A ((t - ti) C 1( t -12) C 2/( t -13) C 3)2/3,(11)

где A – постоянная интегрирования, а C1-C3 – коэффициенты, связанные между собой системой уравнений

C1 + C 2 + C3 = 0,(12)

C 1( t ₂ + 1 ₃ - 2 b / 3 a ) + C 2( t, + 1 ₃ - 2 b / 3 a ) +

+C3(t2 + t -2b/3a) = 0,(13)

C 1( t ₂ - b / 3 a )( t ₃ - b /3 a ) + C 2(^ - b /3 a ) • , ( t ₃ - b /3 a ) + C 3( t, - b /3 a )( t₂ - b /3 a ) = 1. (14)

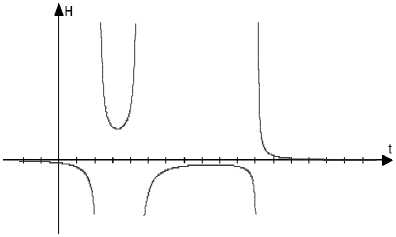
Рис. 1. График зависимости параметра

Хаббла от времени при Q<0

Если Q = 0, то кубический трёхчлен в знаменателях выражений (6)–(7) имеет два различных корня, а масштабный фактор даётся выражением r = A( ea -arcg (t /T) + (t -10)/ a) M,   (15)

M, τ – функции параметров a, b, c.

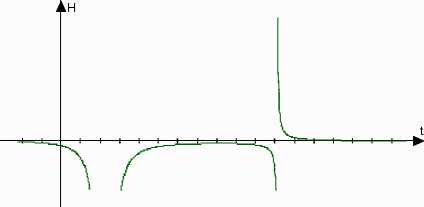
Рис. 2. График зависимости параметра

Хаббла от времени при Q=0

Если Q > 0, то кубический трёхчлен в знаменателях выражений (6)–(7) имеет единственный корень, а масштабный фактор даётся выражением r = Ae ~1/3 a(t - t0)2.               (16)

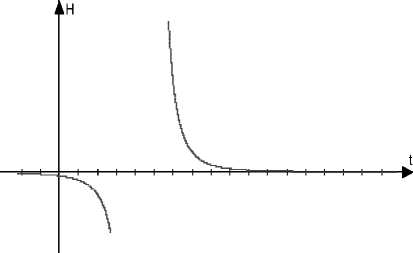
Рис. 3. График зависимости параметра

Хаббла от времени при Q>0

Заключение

По результатам расчётов видно, что моделирование расширения Вселенной с помощью идеальной жидкости с нелинейным уравнением состояния, содержащим квадратичный по времени коэффициент, приводит к появлению в решениях как фантомной, так и нефантомной фаз, а также фазы замедленного расширения, соответствующей положительному давлению материи, как и при моделировании с линейной зависимостью [3]. В отличие от результатов работы [3] здесь наблюда- ется от одной до трёх сингулярностей в зависимости от конкретного вида моделирующей функции.