Краевая задача Гильберта для одного класса обобщенных аналитических функций с сингулярной линией

DOI:

Обозначим: г = ж + гу = ге ^г6 — комплексная переменная, Е = { г : Аг >  0 } — верхняя полуплоскость, Г = {г : Аг = 0 } — вещественная ось, L = {г : ^.г = 0, Аг > >  0 } — мнимая полуось. В области Е рассмотрим частный случай обобщенной системы Коши — Римана

В , U - A ( z ) U = F (г), Л(г) = ^^М, _а(г^,р (г ) ЕС (Е \L).         (1)

Для решений U(_) этой системы в верхней полуплоскости исследуем задачу Гильберта с краевым условием на Г , непрерывными коэффициентом и правой частью. Решение краевой задачи проводим с использованием структурной формулы общего решения системы (1). Эту формулу выводим при достаточно общих ограничениях, допускающих бесконечный индекс сопутствующей задачи Гильберта для аналитических функций. Решение и исследование разрешимости последней задачи составляет вторую часть данной работы.

Теория обобщенных систем Коши — Римана в ограниченной или неограниченной области G с коэффициентами из L^P(G), р >  2, или L^P,2(G), р >  2, и краевых задач для U (z) изложена в монографии [2]. Изучению обобщенной системы Коши — Римана, коэффициенты которой обращаются в бесконечность степенного порядка не ниже первого на некоторой линии L (сингулярной линии) и краевых задач для ее решений, посвящены работы [4–6; 8; 16] и др.

В работе А.Б. Расулова и А.П. Солдатова [11] предложен метод построения обобщенного решения для системы вида (1) с сингулярной или сверхсингулярной линией в конечной односвязной области G с гладкая границей, основанный на купировании линии L семейством областей, исчерпывающих G , с последующим предельным переходом в последовательности построенных классических решений. Под обобщенным решением уравнения (1) будем понимать функцию U ЕС (Е \ L), имеющую первую обобщенную в смысле Соболева производную д ^ класса L^P(K ), р >  2 в каждом компакте К ^ G и удовлетворяющую уравнению (1) почти всюду.

Следует отметить, что в приведенных выше работах рассматривались задачи, приводящиеся к краевым задачам теории аналитических функций с конечным индексом. А.Б. Расулов обратил внимание на то, что краевая задача с конечным индексом для обобщенных аналитических функций с сингулярной линией при решении может трансформироваться в аналогичную задачу теории аналитических функций, но с бесконечным индексом. Эта ситуация описана в работе [7] для задачи Римана на полуокружности и задачи Римана на гладком замкнутом контуре [9]. Приведены формулы общего решения и обсуждается разрешимость краевых задач. Поскольку решение краевой задачи для обобщенных аналитических функций может быть сведено к решению аналогичной задачи для аналитических функций с бесконечным индексом, то требуется разработать метод решения последней для заданной особенности индекса.

Исследованию задачи Гильберта с бесконечным индексом посвящено довольно много работ (см., например, [1; 12; 15]). В основном все результаты получены в случае, когда задача имеет только одну точку завихрения. Случай задачи Гильберта с бесконечным индексом логарифмического порядка и конечным числом точек завихрения рассмотрен в работе [14] для конечной области.

1.    Решение эллиптической системы

Следуя [11], будем предполагать, что для A(z) существует такая аналитическая в Е , ограниченная в Е функция а ₀ (_) , что

A o (z):= “ ^{( Z} )_+‘Z ° ^{( Z} ) e L* 2 (E), р> 2.                        (2)

Граничные значения функции а0(_), то есть функции а0(х), будем считать непрерывными по Гельдеру на интервалах (-то,0), (0, +то), включая концы, в которых эти функции имеют конечные односторонние чисто мнимые пределы. Кроме того, на функции ao(z) дополнительно налагаем следующие ограничения:

|ao(z) — ao(—z)| < К(|z + z|a), ж ^ 0, 0 < а < 1, у > 0;

ao(z) = O(|z|-Y), |z| ^ +то, у > 0, у > 0;

ao(z) = O(|z|у), |z| ^ 0, у > 0, у > 0.

В отличие от [11] мы не требуем непрерывности a _o (z) на Г и обращения в нуль этой функции в точках пересечения линий Г и L . Эти изменения приведут к случаю бесконечного индекса при редукции задачи Гильберта для обобщенной аналитической функции к аналогичной задаче теории аналитических функций.

Выведем формулу общего решения уравнения (1) в области Е методом из работы [11]. Обозначим γ_ε полуокружность в верхней полуплоскости с центром в начале координат радиуса 1/ е , е — малое положительное число, и рассмотрим области Е ± = Е П { z : ±^ z >  е , | z | <  1/ е }. Теперь введем открытое множество Е _е = Е ^ U Е ^- . Граница области Е + состоит из отрезка вещественной оси Г ^ , вертикального отрезка L + = { z : z = е + гу, 0 <  у <  ^¹ -^Е 4 } и дуги у + полуокружности у _е . Аналогичные обозначения введем для участков границы Е ^- .

Обозначим символом Т_£А интегральный оператор Векуа по объединению областей Е_е . Нам нужно убедиться, что (T_£A)(z), z G К, равномерно сходится при е ^ 0 к пределу Q(z) на любом компакте К, К G Е - U Е ⁺ , где Е ± = Е П { z : ±^ z > 0 } . Следуя [11], представим Т_ЕЛ в виде

(ТМ)М = (TM o )W — Л(z), Л(z) = П у AZ) • у--,

Ее причем последний интеграл понимаем в смысле

л (z) = lim ¹            •       , Е_{е 5} = Е, П{| < — z | >  5 } .

^{4 !}   5^0 П     Z + Z Z — z       ^Е,5

^Е е , 8

Входящий в правую часть равенства интеграл преобразуем по формуле Грина

1 Г a o (Z) • Z:z = 1_ П У Z + Z Z — z    2пг

Е е , 8

/+ /+ / )

'е+ дЕ -   | z - t | =5 ⁷

a o (t) ln | t + t |

(Zt.

t — z

После перехода к пределу по 5 ^ 0 получим

Л (z) =

2пг

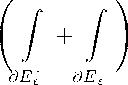
a o (t) ln | t + t | t — z

— a _o (z) In | z + z | .

Рассмотрим в Е+ область Е+, ограниченную отрезком вещественной оси Г+ = = {z = ж, 1 < ж < 1/е}, вертикальным отрезком L+ = {z : z = 1 + гу, 0 < у < < ^1 -Е2} и частью у+ дуги у+. Аналогичную область Е-1 введем в Е-. Поскольку начало координат не принадлежит областям Е^, Е - , формулу для Ie (z) перепишем так:

I. (z) =

f ln I t + t |                f

J -——— do(t^dt + J e +                  se +

In 2t

t

a ₀ (t)dt

-

-

2пг J

In |t + t|     . . , f

---------- a ₀ (t)dt + / t - z            J

^{ln(-2 t )}

---------a + (t)dt — a ₀ (z) In | z + z | .

dE -

dE ^-

Пусть z = ж + гу — фиксированная точка из компакта К и z Е Е +. Выберем е настолько малым, чтобы выполнялись неравенства |z| < 1/е , Kz > е. Рассмотрим входящие в правую часть формулы (6) криволинейные интегралы. Для интеграла по дуге окружности γ+ с использованием условия (4) выводим оценку f ao(t) ln |t + t| dt J t — z

Y +

,9

arccos e ²

/ in ( 1cos’)^

eiedd

— z

C nE ^Y 2

⁵ 2(1 — _E| z | )‘ ⁿ Щ.

Аналогичные неравенства получаем и для остальных интегралов по дугам полуокружности γ . Таким образом, имеет место следующее асимптотическое равенство

/ a o (t) ^ln^ +^{t i} dt + У  lnS® dt = o(e^y inj) ,   e ^ 0.

Y + + Y -                     Y + + Y - 1

Теперь рассмотрим криволинейный интеграл из (6) по L + [J L - , который представим в виде:

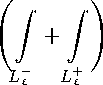
^{a o ( t )ln |t + г|} dt = г in(2 е ) t - z               ^v ’

V 1 — ⁴ / е ∫︁ [︂

a o ( - E + гп) - e + гп - z

-

a o ( e + гп) e + гп - z

] dn.

Отсюда с привлечением условия (3) и ограниченности функции a ₀ (t) выводим

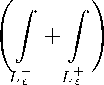
aa o ’^iln^ dt = o(_e a ln 2 ^j ) ,  .   . о.

t - z

Наконец, рассмотрим

L + +L - 1

a o (t) ln(2t) d_t = t

f    a o (1 + гп) ln(2 + г2п) d - f

J           1+ гп          ^X J

a o (—1 + гп) ln(—2 + г2п)

- 1 + гп

dn.

В силу ограниченности функции a ₀ (z) и условия (4) сходятся несобственные интегралы

∞

∫︁

a o (1 + гп) ln(2 + г2п) , -------е—е --------dn = c i , 1 + гп

∞

∫︁

a o (—1 + гп) ln(—2 + г2п) , ---------е—е --------dn = С 2 ,

- 1 + гп

поэтому

J ln^a o (t)dt + J ^{ln( — 2 t )} a o (t)dt = c i - C 2 + 0 ^ E ^a ln ² 1 ) .

9E +             dH —

В равенстве (6), принимая во внимание оценки (7), (8), (9), переходим к пределу по e ^ 0 при фиксированном z E К lim Ie(z) = ε→0

z [ ao (t) In | 2t |     _— 1 1 a o (t) In | 2t |

2П J  t(t — z )      2П J t — z

-∞                    - 1

+∞ z f ao(t) In |2t |

^—   ; ~TT, ----\—^{dt — a} 0 ^{( z}) ^{ln | z + z | + C} 1

2nz J t (t — z)

- 1

— C 2 .

Для интеграла типа Коши с плотностью, имеющей разрыв логарифмического поряд- ка в начале координат, справедлива асимптотическая формула И.М. Мельника (см.: [3,

с. 74])

+1 1    / a o ( t ) ln |2 t | dt = a o (0 — ) — a o (0+) ln 2 1 — 2П J    t — z              4ni          z                  (11) — a o (0+) + a o ( ln 1 + 0(1), z^ 0.

Здесь под In z понимаем однозначную ветвь на разрезанной вдоль Г ⁺ плоскости, принимающую на левой стороне разреза при движении против часовой стрелки значение ln t. Вблизи бесконечно удаленной точки имеем

Отметим, что регулярные составляющие в правых частях формул (11), (12) являются голоморфными в соответствующих областях функциями.

Итак, мы доказали, что при условиях (3), (4) функция I_E(z) равномерно сходится на компакте к пределу (10). Следовательно (см. [11]), обобщенное решение уравнения (1) в области Е в классе функций с ограниченным произведением [/e ^{- Q} задается формулами вида

U (z) = e ^{Q( z )} [(T (e ^{- Q} F ))(z) + ф(z)],                          (13)

где функция

^(z) = (TA o )(z) + ^ / ^{a o ( t )ln |t + t|} dt + a o (z)ln | z + z | ;            (14)

2n^ J     t — z

Г+ интегральный оператор Векуа

(TA o )(z) = —¹ / A^^, z E Е ⁺ , nJ Z — z

E действует [2, c. 44] из LP’2(E), р > 2, в класс Гельдера Н(Е); функция ф(г) аналитична в Е. Итак, доказано следующее утверждение.

Теорема 1. Пусть коэффициент А(г) уравнения (1) удовлетворяет условиям (3)-(5), то общее решение уравнения (1) в области Е в классе функций с ограниченным произведением Ue ^{- Q} задается формулами (13), (14), ф(^) — произвольная аналитическая функция в Е \ L .

Обозначим односторонние пределы функции а ₀ (ж) в начале координат и в бесконечности символами: а ₀ (0+) = гр + , а ₀ (0 — ) = гц - , а ₀ (+ то ) = iv + , а ₀ ( —то ) = iv — . В соответствии с равенствами (14), (11), (12) для функций Q(z) вблизи начала координат справедлива формула

^(г) = Р—-—— ln²-- г Р— +_Е ± ln —+ а ₀ (г) ln | г + г | + 0(1), г ^ 0,

4п г 2 г и вблизи бесконечно удаленной точки — формула

^(г) =

v - — v ±

4п

ln ² г + г

V - + v ± 2

lnг + a ₀ (г)ln | г + г | +0(1), | г | ^ + то .

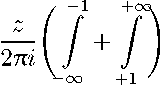
a _o (t) ln | 2t | t (t — z)

dt

a o (—to) — а о (+ то ) 4П

ln ² z +

+      ' + ^a ' lnz + 0(1), kH + w .

Отсюда выводим

^——— ln ² — - ^{г 2р}- ln — ^{+ 0 (1)} , ^t ^ ^0— ,

0(t) =         ⁴_^п         It    ,    .,.1*1 .

р—ln2 — г '■ + ц ln - + 0(1), t ^ 0+, 4п       t2

-------± ln2 |t| + i2v— ln |t| + 0(1), t ^ —to, fi(t) =         ,n               ,.

——V± ln2t + г3v± + V- ln t + 0(1), t ^ +to, 4n2

Для обобщенного решения уравнения (1), заданного формулами (13), (14), где ф(г) — произвольная аналитическая функция в Е, непрерывная в Е, рассмотрим в полуплоскости Е задачу Гильберта с краевым условием на вещественной оси

W-^U(t)] = /(t),   t G Г,

непрерывными по Гельдеру всюду на Г , включая бесконечно удаленную точку, коэффициентом е ^{га (}*) и правой частью /(t) . Подставляя функцию (13) в краевое условие (17), получим краевое условие задачи Гильберта для определения аналитической в полуплоскости функции ф(г) :

^ [e ^гa * < ^{^ )} ф(t)] = / * (t), t G Г, t = 0,t = to, a * (t) = a(t) + A Q(t),

/ * (t) = / (tK³^ — W^{i a} * ^(tHT (e ^{- Q} F))(t)].

Из формул (15), (16) выводим следующие равенства:

a * (t) = <

2v — ln | t + г | + ф (*),    t G (—to, — 1), 1 —2ц - ln — + г + ф(t), t G (— 1, 0), —P —f^^ ± ln 1+ . + ф((),  t G (0,1),               (l9) 2           t V- + 3v± , . 2      ln | t + г | + y(t),   t G (1, +to),

/ * (t) =

/(t)exp| ^{v    v} ln ²

4П

/(t)exp | "^ ln ²

4П

Hj- + ф⁽^, | 1 | } ' Ш,

t G (—to, 1) U (1, +to), t G (—1, 0) U (0, 1),

в которых функции ф(t), ф(t) удовлетворяют условию Гельдера всюду на Г , включая бесконечно удаленную точку, то есть принадлежат классу Н _г . От функции /(t) требуем дополнительно выполнения условий

/(t)exp| ^{V +} _{4 n} ^V ln ² | t|J / ^{( t )ex} p| ^{S +} _{4 n} ^{S ln} и}

= o(1),

= o(1),

| t | ^ to, | t | ^ 0.

Таким образом, задачу (17) сводим к краевой задаче Гильберта (18) для аналитических функций с бесконечным индексом и двумя точками завихрения в начале координат и в бесконечно удаленной точке.

2.    Решение задачи Гильберта2.1.    Однородная задача

Вначале рассмотрим соответствующую (18) однородную задачу. Требуется найти аналитическую и ограниченную в полуплоскости Е функцию ф(г), по краевому условию

№ [e ^ia *⁽^ (t)] = 0, t G Г \ ( { 0 } U {то} ),

в котором для a * (t) справедливы формулы (19). Наряду с задачей (21) рассмотрим две краевые задачи для аналитических в Е функций, с одной точкой завихрения каждая:

^ [_е ' ^а * <^) ф о (t)] = 0,

^a 0 ^{( t )} = <

—2p ln — + г + ф(t), t G (—1, 0),

^S ₂ 3 ^{S + ln 1} + ^г + Ф⁽^, ^{t G (0 , 1)} ,

Ф ^{( t ) , | t |} > 1,

	2v ln | t + г | + ф(t), t G (—to, — 1),
№ [e ia *(^i (t)] =0,   a l (t) = <	Ф(^, | ^ | <  1,                                           (23) v- +3v+ . , 2      ln | t + г | + ф(t), t G (1, +to).

В работе [14] доказано, что однородная краевая задача Гильберта (21) с двумя точками завихрения логарифмического порядка разрешима в классе аналитических в Е и ограниченных в Е функций ф(^), если и только если разрешимы в классе аналитических в Е и ограниченных в Е функций обе однородные задачи Гильберта (22), (23), с одной точкой завихрения логарифмического порядка каждая. При этом общее решение задачи (21) по существу можно представить в виде произведения решений задач (22) и (23). Задача (23) хорошо изучена (см., например, работы [1; 15]). Возьмем формулу общего решения задачи (23) из статьи А.Г. Алехно [1], которая в наших обозначениях будет выглядеть так ф1(z) = /г z' '' ' r '' /<( z), (24)

где

R i (z) := -^-(v + - V — ) 1n ² (z + г) — г 1Z + +2^-. ^(z + г), 4п                      п

Г г (г)

+ ^ п/

h^ (t)dt t — z ’

h ₁ (t) := — a 1 (t) — 3R ₁ (t), h ₁ (t) G H _r .

-∞

При этом формула (24) содержательна, если v ₊ — v - <  0. Именно,

• а)    если V - — v ₊ > 0, то задача (23) имеет бесконечное множество ограниченных решений, которые задаются формулой (24), где F ₁ (z) — сужение на верхнюю полуплоскость произвольной целой функции уточненного нулевого порядка р(т) = 1п1п ² т/ 1п т, принимающей на Г действительные значения и удовлетворяющей неравенству

  | F i (t) | <  С exp 13 ^V ' , /   1п ² | t + г|},

  
  

  С = const, t G Г;

  
  
  
  

• б)    если V - — v ₊ = 0, то задача имеет единственное решение вида Ф 1 (г) = — гЛе ^{г( г )} , Л = const , З А = 0.

При V - — v ₊ < 0 задача (23) не имеет решений в классе ограниченных аналитических функций.

Формула общего решения и картина разрешимости однородной задачи (22) получается из формулы (22) и картины разрешимости задачи (23) при помощи конформного автоморфизма Z(г) = — 1/z полуплоскости:

фo(z) = — V''     + F z), где

R o (z) := R о Z(z), R«) := 4П(^ - — _{и +} ) 1п ² (Z + г) + г ^ - 1n(Z + г),

^Г o ^{( z ) :} =

+ ^

П /

h _o (t)dt t — z ,

^h o ^{( t ) :} = ^—a 0 ^{( t ) — 3 R} o ^{( t )} , ^h o ^{( t ) G H} r ,

-∞

Fo(z) — аналитическая в E функция, ограниченная всюду, кроме полуокрестности точки t = 0, в которой имеет рост не больше, чем С1ес'2ln |z +г|, и на Г удовлетворяющая условиям

3 F o (t) = 0,

| F o (t) |< Cexp{ ³⁽ ^ 4 — ^ ^{+ )} 1п ² | t ¹ + г | }.

Картина разрешимости задачи (22) такая же, как у задачи (23).

С учетом вышесказанного, при выполнении условий р- - Р+

V + — V -

> 0,

> 0,

запишем формулу общего решения однородной задачи (21):

+ ^

ф(=) = -ie-W^V^F (г), Г(г) := ¹ j ^{h o (}^ + ^) dt,

-∞

F (г) — аналитическая в Е функция, удовлетворяющая ограничению роста

| F(г) | < C i e ^c 2 ^(ln 2 ^{| г} 1 ^{+ i | +ln} 2 ^{| z + i | )} ,                                      (28)

и на Г — условиям:

^F (t) = 0, | F(t) |< C exp ^ ^{3(р -} --^{р +}- ln ² | | + z | + 3 ^{( v}+₄^{— V} ) ln ² I t + ® | } .     (29)

При этом, если хотя бы одно неравенство в (26) строгое, то однородная краевая задача Гильберта (21) имеет бесконечное множество решений вида (27). В противном случае решение задачи единственно с точностью до постоянного вещественного сомножителя и получается по формуле (27), в которой нужно взять F (г) = А , А = const. Если условие (30) не выполнено, то задача (21) не разрешима в классе ограниченных аналитических функций.

2.2.    Неоднородная задача

Перепишем краевое условие (18) неоднородной задачи в виде

^ [е- г +ГО e ^{- ( R o ( t )+ R 1 ( t)}^ (t)j = у * (t)e ^{-r a (t)} Ie ^{-(R o (t)+R 1 (t))} I,

где

Г ⁵

+ ^

(t) = П /

h o (T) + h i (T)

т — t

dT.

-

∞

Будем считать, что однородная задача (21) разрешима, что эквивалентно разрешимости задач (22), (23). Нам понадобится каноническое решение однородной задачи, (21), то есть ограниченное решение, для которого входящая в формулу (27) функция F (г) кроме условий (28), (29) дополнительно удовлетворяет ограничениям

| е - ^{( R} o ^{( t )+ R} i ^{( t ))} |                                     | e^{- ( R} o ^{( t )+ R} i ^{( t ))} |

^{F ( t )} = ⁰ ;   lim-----БТм----= ^m, ⁰ <^m< ^TO;  ----- FTA ---- ^{G Я} г .      ⁽³¹⁾

t ^^       ^F (^t)                                      ^F (^t)

При этом функцию F (г) можно искать в виде F (г) = F ₀ (г)F ₁ (г). Для построения F ₁ (г)

возьмем целую функцию

fl 6 — —) 1=1        _{Т к} ^е« ^ф 1

с произвольно фиксированным ф ₁ , 0 < ф ₁ < п, для которой через п(г) обозначим число нулей в круге | z | <  г . Следуя [15], считающую функцию определим формулой

п(г) = <

Е(1/2 + А1 lnг), г > 1,

0,   0 < г < 1, где Е(t) — целая часть числа t, то есть г. = e((k 1/2)/А1), фиксированную величину А1 > 0 выберем позже. Для целой функции ад = П f1 - ^) f1 - ^), г. = e^,     (32)

в [14] для функции (32) доказаны формулы lnF1(z) = А1 ln2 |z| + O(ln |z|), |z| ^ +то,                      (33)

ln | F* 1 (t) | = {

ln ² 1 [ A i + 2п ² Ао ( ^ln 2 Н [ ^А 1 + ^п 2 ^А о (

# + - - 1 ) ln - ¹ 1 + п(ф> 0,

2п ²    п 3

ф ²     1

П ^{1 +} з) ^{ln 1} М ^{+ г} 2 ^{( t)}] , ^t<  ⁰

Отметим, что г ₁ (t) = O(ln ^{- 2} t), t ^ + то , г ₂ (t) = O(ln ^{- 2} | t | ), t ^ —то и функции г ₁ (t), г ₂ (t) непрерывны по Гельдеру в области своего определения (см.: [14; 15]). Из формулы (33) следует, что целая функция F ₁ (z) имеет уточненный нулевой порядок р(г) = lnln ² г/ ln г, ее мнимая часть обращается в нуль навещественной оси (по построению) и в силу (34) при А ₁ = 3(v ⁺ — v ^- )/4n удовлетворяет условиям (29), (31). Для построения функции F ₀ (z) = F о Z(z) определим F (Z) в верхней полуплоскости из формулы (33), заменив А ₁ на А _о = 3(^ ⁺ — ц ^- )/4п. Теперь мы определим функцию F (z) = F ₀ (z)F ₁ (z) и по формуле (27) — каноническое решение однородной задачи (25)

ф^) = — i/ ^{r( z )} e ^fi 0 ^{( z )+ fi 1 ( z )} F(z).

Краевое условие неоднородной задачи (30) после деления на F (t) выделения в знаменателе левой части функции ф(t) примет вид

_$ L,±(*)1 = _C(t>  _C(ti = / * (tjie-^^

[ ф(t)]    ^U’ ^U        e^r^^F(t)

Будем искать частное решение неоднородной задачи, имеющее те же последовательности нулей, что и функция F (z) и, следовательно, ф(z). Поэтому отношение ф(z)/ф(z) для искомой функции будет аналитической и ограниченной в Е функцией. Поскольку c(t) G G Н _г , функция — гф(z)/ф(z) представима по формуле Шварца, то искомое частное решение представимо формулой

ф(z) = — ,e ^r<') e ^R > <')⁺« i <'). F(z) ¹ f ^{C 1 ( t}^.

L

Последняя формула дает частное решение неоднородной краевой задачи (30), общее решение которой представим в виде суммы общего решения соответствующей однородной задачи и данного частного решения:

ф(г) = - ,_е г<-> _е Л о <»>+» 1И (f (z) ₊ F(_Z)1 у ^C-1^\ .

L

Итак, справедлива следующая теорема.

Теорема 2. Если выполнены условия (20), (29), то неоднородная задача (30) разрешима в классе ограниченных аналитических в D функций. Общее решение задачи представляется как сумма общего решения (27) однородной задачи и частного решения (35) неоднородной задачи.

Обратимся теперь к задаче (17) для обобщенного решения (13) системы (1). Из доказанной теоремы сразу вытекает следующее утверждение.

Теорема 3. Пусть для коэффициентов уравнения (1) выполнены условия (2)–(5) и (e~ⁿF )(z) G L^{P,, 2} (E ), р >  2, односторонние пределы на бесконечности функции а ₀ (х) удовлетворяют системе неравенств (26). Тогда, если хотя бы одно из неравенств (26) строгое, а правая часть краевого условия (17) имеет асимптотику (20), то задача Гильберта (17) имеет бесконечное множество решений U(z ), определенных формулой (12) с ф(z ) в виде (35). Если же в (26) v - — v ⁺ = 0, ^ - — ^ ⁺ = 0, то задача имеет единственное с точностью до постоянного вещественного сомножителя решение и определяется формулой (12) с ф(z) в виде (35), в которой F (z) = const.