Краевые задачи для смешанного параболо-гиперболического уравнения четвертого порядка с разрывными условиями склеивания
Автор: Абдумиталип Уулу Кубатбек
Журнал: Бюллетень науки и практики @bulletennauki
Рубрика: Физико-математические науки
Статья в выпуске: 11 т.8, 2022 года.
Бесплатный доступ
Доказана теорема существования и единственности решения краевой задачи для уравнения в частных производных четвертого порядка с переменными коэффициентами, содержащее произведение смешанного параболо-гиперболического оператора и дифференциального оператора колебания струны с разрывными условиями склеивания в пятиугольнике на плоскости. Методом понижения порядка уравнений разрешимость краевой задачи сводится к решению задачи Трикоми для смешанного параболо-гиперболического уравнения с переменными коэффициентами и с разрывными условиями склеивания. Разрешимость этой задачи сводится к решению интегрального уравнения Фредгольма второго рода относительно следа производной функции по y на линии изменения типа уравнения. В гиперболической части области методом функции Римана получено представление решения задачи для гиперболического уравнения с младшими членами. В параболической части области методом последовательных приближений и функции Грина получено решение первой краевой задачи для параболического уравнения с младшими членами. В результате решение задачи реализуется методом решения задачи Гурса и первой краевой задачи для уравнения колебания струны.
Краевые задачи, параболо-гиперболический оператор, интегральные уравнения, функция римана и грина
Короткий адрес: https://sciup.org/14126123
IDR: 14126123 | УДК: 517.956.6 | DOI: 10.33619/2414-2948/84/01
Текст научной статьи Краевые задачи для смешанного параболо-гиперболического уравнения четвертого порядка с разрывными условиями склеивания
Бюллетень науки и практики / Bulletin of Science and Practice
УДК 517.956.6
1. Постановка задачи. В области D , ограниченная отрезками линий АС:х + у = 0,СВ:х — у = 1(1 > 0),ВВ0:х = 1,В0А0:у = h(h > 0),А0А:х = 0, рассмотрим уравнение
L1L2u = 0
L 1
{ I = -^ + а (х, у) V- + с (х, у), у > 0,
1 дх2 ду 1 дх 1
1 2 = дХ; - дУ; + а 2 (х,у) дх + Ь 2 (х,у) ду+ ^^
l =д_
2 дx2
а 2
ду2 ’
где а1(х,у),С{(х,у)(1 = 1,2),Ь2(х,у) — заданные функции, удовлетворяющие условиям:
а 1 (х,у),а 1х (х,у),а 1у (х,у),С 1 (х,у) е C(D 1 ), (2)
а 2 (х, у), а 2х (х, у), Ь 2 (х, у),Ь 2у (х, у), С 2 (х, у)С^).
Пусть D1 = D П (у > 0), D2 = D П (у < 0) . Класс Сп+т означает существование и dr+s непрерывность всех производных gxrgyS (? = 0,1,..., n;s = 0,1,..., т) [1].
Уравнение (1) в области D1 представимо в виде д2 д д д2 д2
hL2 ^ (дх2—ду + а1(х’у)Тх + с^jw-wr0^'^ D и имеет двукратную характеристику у = const и две различные характеристики х + у = const, х — у = const, а в области D2 примет вид д2 д2 д д д2и д2и (4)
l 2 L 2 ^[дX 2 — дУ 2 + а 2 (х, у)дх + Ь 2 (х, у)ду+С 2 (х, у))[д? — ду 2 )
= 0, (х, у) е D 2
причем имеет две различные двукратные характеристики: х + у = const, х — у = const [2].
В области D для уравнения (1) рассматривается
Задача 1. Требуется найти функцию и(х,у) со следующими свойствами:
-
1) и(х,у) является решением уравнения (1) в области D\(у = 0);
-
2) и(х,у) и ее частные производные первого порядка непрерывны в области D ;
-
3) функция u = u xx u yy непрерывна в области D\(y = 0);
∂ u ∂ u
-
4) функции д x и д y непрерывна в области D\(y = 0); ∂ u
-
5) для функции □и и d y на линии у = 0 выполняются следующие разрывные условия склеивания:
□и(х, -0) = а(х)пи(х, +0) + у(х),0 < х <1, д^и(х, -0) д^и(х, +0)
ду ^(х) ду + (хх^° <х < где а(х), @(х),3(х), у(х) — заданные функции, удовлетворяющие условиям:
Ух е [0,1]: а(х),Р(х),у(х),8(х) £ С[0,/],а(х)^(х) Ф 0;
-
6) и(х,у) удовлетворяет следующим условиям:
u|AA =ϕ1( y), u|BB =ϕ2(y), 0≤y≤h,(7)
uxx |AA0 =ϕ3( y), uxx|BB0=ϕ4(y), 0≤y≤h,(8)
и1АС =-ф1(х),0 < х <1, и1вс = ^2(х),1 < х < I, ди дп ВС
I
= ^ з (х),-<х<1
где п — внутренняя нормаль, ^i(y)(i = 1,4,^-(х^ = 1,3) — заданные функции, причем:
^ i (y) е c2[0,h](i = 1,2),^}(у} е C[0,h](j = 3,4),
^ 1 (х) е С [0,|],^ , (х)
ес2[1,1],^3(х)ес3[1,1];
^ 1 (0) = Ф^ШЪ = ^ 2 (0), Ф 1 (1) = ^ 2 (£), а(1)[^ 4 (0) - ^2'(0)] + Y(f) = -JW’W-
Краевые задачи для уравнений L 1 u = 0, L 2 L 1 u = 0 рассмотрены в работах [3, 4].
Краевая задача для уравнения (1) с постоянными коэффициентами и с непрерывными условиями склеивания, изучена в работе [5].
Краевые задачи для уравнения 1 1 12и = 0, в случае, когда оператор L 1 представляет собой эллиптико-гиперболический оператор, изучены в работах [6, 7].
Краевые задачи для уравнения типа (1), когда L1 — эллиптико-гиперболический, а L2 — дифференциальный оператор n-порядка, исследована в работе [8].
Краевые задачи для уравнений смешанного типа с разрывными условиями склеивания впервые изучены в работах [9, 10].
При у > 0 уравнение (1) запишем в виде системы:
д2и д2и (13)
^^^-^^^'У)’^’^0!’ д2v1
l1V1 = ~Х^
-
дv1
— + а1(Х'У)ь1х + с^Х'У^ ! = О, (Х’У) Е 0 1 ; ду
-
а при у < 0 в виде следующей системы:
д2и д2и(15)
ь2и ^ дХ2 - ду2 = v2(Х’ У)’(Х’ У) ED2’ д2v2 д2v2 дv2 дv2(16)
l 2 V 2 = ^Х 2 - ~дУ 2 + а 2 (Х’У)~дХ + Ь 2 (Х’У)1У + C 2 (Х'У^V 2 = 0’ (Х’У) ED 2 .
Из граничных условий (7), (8) получим:
Vilx=o = Ф1(У)’V1|х=f = Фг^У^’О <У<Ь’ где ф1(У) = ф3(у) - Ф1(У)’ Ф2(у) = Ф4(У) - Ф2(У). Условие (10) запишем в виде
I v2(Х’ х — 1) = —\2ф3 (х)’ -< х < I.
Таким образом, для определения функций v1(X’У) и v2(X’У) придем к следующей задаче.
Задача 2. Найти функции v1(Х’У) и v2(x,у), удовлетворяющие следующим условиям:
-
1) V 1 (Х’У) е С(0 1 ) П С2+1(0 1 ), V 2 (Х’У) Е С(0 2 ) П C2(D 2 );
-
2) v1(Х’У) является решением уравнения (14) в области D 1 , а v2(Х’У) является решением уравнения (16) в области D2 ;
-
3) для функций Vi(xlу)’^^(x^(^ = 1’2') на линии у = 0 выполняются разрывные условия склеивания:
v2(X’—0) = a(x)v
1
(X’ +0) + у(х}’0
ev^^—0)=Д(x)дV
1
^X+0) + ^(x)'0
-
4) функция v1(X’У) удовлетворяет условиям (17),а v2(X'У) удовлетворяет условию (18).
-
2. Соотношение между g1(x') и 0 1 (x), полученное из области D 1 .
Для решения задачи 2 введем новые неизвестные функции следующим образом: v 1 (X’+0) = ^1(x)’v2(X’-0) = ^2(x)’v1y(X’+0) = 01(x)’ v2y(X’-0) = = 02(x)’0 < x < I. Тогда условия склеивания (19) запишется в виде:
Бюллетень науки и практики / Bulletin of Science and Practice Т. 8. №11. 2022 g2(x) = a(x)g1(x') + y(x),0 < x < l, (20)
02(х)=^(х)01(х) + 3(х),О<х<1 (21)
Сначала рассмотрим задачу 2. Переходя к пределу при у ^ +0, из уравнения (14), получим соотношение между функциями g 1 (x) и 0 1 (x):
g " (x) + a 1 (x, 0)^ 1 (x) + c 1 (x, 0)g 1 (x) = 0 1 (x),0 < x < l.
Из условия согласования имеем:
14(0) = $ 1 (0),I4(l) = $ 2 (0).
Полагая
x
^ i (x) = $ 1 (0) + J [$ 2 (0) - $ 1 (0)] + z(x),
I где z(x) — новая неизвестная функция, задача (22), (23) сводится к следующей задаче z"(x) + a1(x, 0)z'(x) + c1(x, 0)z(x) = g(x),
z(0) = 0,z(l = 0, где g(x) = 01(x) - C1(x,0)$1(0) - -[$2(0) - $1(0)][a1(x,0) +xC1(x,0)]
Теорема 1. Если a 1 (x, 0), a1x(x, 0), c 1 (x, 0) £ С[0, l] и
Vx £ [0, l]: C1 (x, 0) — I a^ (x, 0) < 0, тогда задача (25), (26) имеет единственное решение.
Доказательство. Рассмотрим однородное уравнение (25). Умножая это уравнение на z(x) и интегрируя полученное равенство по x от 0 до l, имеем тождество:
fo{[z ' (x)]2 - [c 1 (x,0)- 1 a 1x (x,0)]z2(x)}dx = 0.
Отсюда при выполнении условия (27) заключаем, что Vx £ [0,l]:z(x) = 0. Теорема 1 доказана.
Решение задачи (25), (26) представим в виде [11]
z(x) = [ G1(x,t)g(f)df, 0
где G 1 (x,%) — функция Грина. Тогда из (24) и (28) имеем соотношение между g 1 (x) и 0 1 (x), полученное из области D 1 в виде:
V i (x) = g iW + I G i (x,Q Qi^d^, 0
где
Ф 1 (0)] х
9
i
(x) =
i
(0)+
X
[^(0) — i(0)] — J0lGi(x,%){^^i(0)ci(%,0)+1[^2(0) — x[a1(%,0)+%c1(%,0)]}d%. 3. Соотношение между ^(x') и 02(x), полученное из области D2. Решение задачи Коши для уравнения (16), удовлетворяющее условиям v2(x,—0) = 92(x), v2y(x,—0) = 02(x),0< x < l, имеет вид [12, 13]: »2(x,y) = - [R(x,y;x + y,0)^(x + y) + R(x,y; x — y,0)^2(x — y)] + 1 X-y + 5 I [R^(x,y;^0) + b2(C0)R(x,y;^0)]^«M — 2 X+y 1 X-y — 5 I R(x,y;%,0)02<%)d%, 2 X+y где R(x,y; %,r) — функция Римана, которая определяется как решение следующей задачи Гурса: RK - Rw - (a2R}^ - (b2R\ + C2R = 0, «,7?) e D*, R(x,y;^,r)\n=x+y—f = exp{—|| [a2(t,x + y — t) + +b2(t,x + y — t)]dt},x + y < % < x, R(x,y;%,r)\v=^—x+y = exp{|| [a2(t,t — x + y) — —b2(t, t — x + y)]dt},x < % < x — y, R(x,y; x,y) = 1. где D2 = {(%,r): y < Г < 0, x + y — r < % < x — y + r}. Используя условия (18), из (30) имеем R(x,x — I; 2x — I, 0)g2(2x — l) — R(x,x — l; I, 0)V2^3(l) — 2X—1 I [R^(x, x — l; %,0) + b2^, 0)R(x,x — I; %, 0)]^«M + l 2X—1 l + I R(x,x — l;%,0)02(%)d% = —2^2^‘.(x),- l2 Пусть 2x — I = z. Тогда x = ^+^. Так как 1< x < I, то 0< 2x — l /z + l z — l \ f z Г /z + l z — l \ R(——r^H, r——;<•»)+ /z + l z— I M Zz zz + £ z — I \ +Ш. 0)R (—,—; €• 0)] fe(m — , R (—,—; €, 0) 0 <№ — /z +1\ zz + ^Z-f 2^4 , j.^l , , ., ;l, 0)^(0 , 0 < z < l. Отсюда, заменяя z на x, имеем (x + l x — l \ Xх \ / x + l x — l \ R(—R+ /x +1 x — l \1 Xх /x + l x — l \ +b2 (€ 0)R (—, —; €, 0)] ^2 (€M — , R (—, —; € 0) 02 (€M — x + l\ /x + l x — l —^Ц—) + V2R(— — ;l. 0)^(0 ,0 < x < l. Имеет место следующая Теорема 2. Vx £ [0, l]: x + l x — l R(——R>0 Доказательство. Условие (32) представим в виде R(x,y;€,x + y — €) = exp{—1, ^fcx + y — t) + +b2(t, x + y — t)]}dt, x + y < € < x. Полагая € = x + у,из (38) имеем 1 x R(x,y; x + y, 0) = exp{ — — , [a2(t, x + y — t) + b2(t, x + y — t)]}^t. 2x+y Для удобства рассуждения запишем уравнение прямой СВ: x — y = l f в параметрическом виде: x =^,0 < 5 < l, y^^^l. Заметим, что % + у = s. Тогда из (39) имеем: r( s + l s — , l 1 ^ — ;s, 0) = exp , [n2(t, s — t) + b2(t, s — t)]dt ,0 Отсюда, заменяя 5 на x, убеждаемся в справедливости неравенства (37). Учитывая неравенство (37), уравнение (36) представим в виде ^(х) = \\(x,V^dl;+ С ^ X X х ^(Х.^^ + Ф^х) где Ъ(х,0 = /x+l x-l - л\ , sri\T—X+tX-t г гЛ I^J-’J-^)^^ x+l x-l , R(——;X’0) М 2(х, О I(^Q ^^у Ф1(х) = -2V2^(X)+V2R(^,^; l,0)p'3(l) x+l x-l r(——-’x,0) Обращение интегрального уравнения Вольтерра 2-го рода (40) относительно р.2(х) имеем ^2(х) = Ф2(х) + ( Т1(х,^) X 02^, где Т1(х,0 = Ы2(х,() + /XR1(х,t)N2(t,^)dt, Ф2(х) = Ф1(х) + /X ^1(х,^) Ф1(^)d^ , а Н1(х, ^) — резольвента ядра М^х, ^). Соотношение (41), представляет собой связь между ^(х) и 02(х), полученное из области D2. 4. Сведение задачи 2 к интегральному уравнению. Исключая 01(х) из (21) и (29), имеем д1(х') = fX^^^^d^ + д1(х) — /^^^^^.(х,^ d^. Подставляя найденное выражение для ^1(х) в (20), получим: ^(х^) l8(Q ^2(х) = а(х)1 02(€№ + а(х)[д^х) — I G1(х,^)d^l 0 р(>) 0 Р(^) + У(х). Исключая ^2(х~) из (41) и (42), получаем интегральное уравнение Ст1(х,^02(№ = ^'т2(х,^)02(()d^ + Ф3(х), X 0 где Т2(х,1) = ^(X)G1(х,^), Фз(х) = а(х) [д1(х) — /Х^С1(х,^>d^] + у(х) — Ф2(х). Продифференцирую (43) и учитывая при этом равенство Т1(х,х) = М2(х,х) = —1, имеем Щх)= Ст3(х,О02(Ш+ Ст4(х,О02(Ш + Ф'з(х) X 0 где Тз(х,^) = Т1x(х,(),Т4(х,() = —Т2x(х,^). Обращая Вольтерровскую часть уравнения (44), получим 02« Ст(х,О02(Ш + Ф^х) где Т(х, t) = Т4(х, <0 + f R2(x, t) T4(t, ftdt, Ф4&) = -Ф3 (х) - f R2 (х, <)Ф3(<)d< , R2 (х,<) — резольвента ядра Т3 (х,<). Пусть 1|Т|| = maхlT(х,<)\. 0<Х<1 0 Теорема 3. Если выполняется условие *-m Щх) = Ф5 (х) + С R3(х,^Ф5(^d<, где R3 (х,<) — резольвента ядра Т(х, t). После определения 02(х') по формуле (47), из формул (21), (29), (20) последовательно определяем 01(х'),^1(х'),^2(х') соответственно. Таким образом, существование и единственность решения задачи 2 доказана. 5. Решение задачи 2 в области D±. Из постановки задачи 2 в области D1 для V1(x,y) получим следующую первую краевую задачу для параболического уравнения: I1V1 = Vixx - Viy + ai(x,y)Vix + Ci(x,y)vi = 0, (x,y) E Di, (48) Vi\x=o = Vi(y),Vi\x=t = Ф2(у),0 где Ф1(у) = фз(у)-vily^^y) = Ф4(у)- ^2(y). Теорема 3. Если ^(x,y) E D1: a1, a1x, c1 E C(D) и выполняются условия Ci(x,y) --aix(x,y) < 0, тогда задача (48), (49) имеет единственное решение. Доказательство. Рассмотрим однородные краевые условия (48). Умножая уравнение (48) на v1(x,y) и интегрируя полученное тождество по области D1, имеем тождество: — ffDiViliVidxdy = f^ dx f0h {vlx — [ci(x,y)-1aix(x,y)]v2}dy + 1f0hv2(x,h) = 0. Отсюда, при выполнении условия (50), заключаем, что V(x,y) E D1:V1(x,y) = 0. Теорема 3 доказана. Доказательство существования решения задачи (48), (49) устанавливается следующим образом. Введем новую функцию w(x,y):
Бюллетень науки и практики / Bulletin of Science and Practice
Т. 8. №11. 2022
Тогда уравнение (48) сводится к уравнению Wxx -Wy + C1(x,y)w = 0, где Ci(x,y) = Ci(x,y) - 1alx(x,y) - 1a2(x,y) + 1f^ aiy(^,y)d^. Краевые условия (49) преобразуется к виду: wlx=o = $i(y\w\x={ = ^(y),0 где Ф2(у) = Ф2(у) exp (^ai^^df), fii(x) = Pi(x} exp (j Joxai(f,0)df). Используя для решения задачи (52), (53) функцию Грина первой краевой задачи для уравнения теплопроводности, имеем w(x,y) = f(x,y) + J dp J" oo K(x, y; %, p)w(f,p)df, где K(x,y;t,p) = Citf^G&y^p), f(x,y) = ^0 G^(x,y; 0,p) $i(p)dp - -J G{(x,y;l,p)^2(p)dp + J G(x,y;f,0') pi(f)df, oo G(x,y; ^ = ^t&tf^ lexp (-^^xf} -exp ( Заметим, что для ядра уравнения (54) имеет место оценка V(x,y) e DiKV(^,p) e Di: \K(x,y;%,p)\ < ФФ-Ф )] -функция Грина С i, (y - p)2 где С — положительная константа. Поэтому уравнение (54) является интегральным уравнением типа Фредгольма со слабой особенностью, она разрешима и имеет единственное решение, которое строится методом последовательных приближений [15]. 6. Решение задачи 1 в области D2. Решение задачи 1 в области D2 определим как решение задачи Гурса для уравнения (15), которое представимо в виде: x-y x + y + 1 I u(x,y) = ^i \^~) + Ф2 (---2---) - ^i (2) + + 4 x+y x-yf + P f-P J, ^J V2(——}dP- Отсюда при y = 0 имеем x T(X)= ¥1 - + ^2 V 2 J ' x + T V 2 J — *1 [ 2 J xx +~4\ d^u I £+2, n) V 2'2 J dp. Аналогичным образом, из (55) находим и v(x) = uy(x, 0). u(0, y) = ^(y), u(/, y) = ^2(y), 0 < y< h, u(x,0) = t(x), uy (x,0) = v(x),0 < x< Л Решение этой задачи определяется методом разделения переменных [13]. Таким образом, имеет место Теорема 4. Если выполняются условия (2), (6), (11), (12), (46) и (50), тогда решение задачи 1 существует и единственно.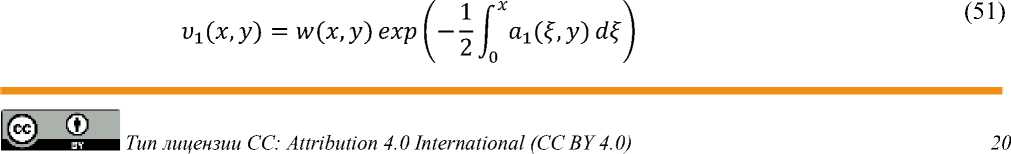
Список литературы Краевые задачи для смешанного параболо-гиперболического уравнения четвертого порядка с разрывными условиями склеивания
- Жегалов В. И., Уткина Е. А. Об одном псевдопараболическом уравнении третьего порядка // Известия вузов. Математика. 1999. №10. С. 73-76.
- Джураев Т. Д., Сопуев А. К теории дифференциальных уравнений в частных производных четвертого порядка. Ташкент: Фан, 2000. 144 с.
- Джураев Т. Д. Краевые задачи для уравнений смешанного и смешанно-составного типов. Ташкент: Фан, 1979. 240 с.
- Джураев Т. Д., Сопуев А., Мамажанов М. Краевые задачи для уравнений параболо–гиперболического типа. Ташкент: Фан, 1986. 220 с.
- Абдумиталип уулу Кубатбек. Краевая задача для смешанного параболо- гиперболического уравнения четвертого порядка с оператором колебания струны // Вестник ОшГУ. Математика, физика, техника. 2021. №2. C. 11-20.
- Бобылева Л. А., Смирнов М. М. Об одной краевой задаче для уравнения смешанно– составного типа 4-го порядка // Известия вузов. Математика. 1972. №5. C. 15-21.
- Смирнов М. М. Краевая задача со смещением для уравнения смешанно–составного типа 4-го порядка // Дифференциальные уравнения. 1975. Т. 11. №9. С. 1678-1686.
- Жегалов В. И. Некоторые задачи для уравнения смешанного-составного типа в бесконечной области // Труды семинара по краевым задачам. 1972. Вып. 9. С. 75-85.
- Жегалов В. И. Краевая задача для уравнения смешанного типа с граничными условиями на обеих характеристиках и с разрывами на переходной линии // Ученые записки Казанского университета. 1962. Т. 122. Кн. 3. С. 3–16.
- Каратопраклиев Г. Об одном обобщении задачи Трикоми // Доклады АН СССР. 1964. Т. 158. №2. С. 271-274.
- Денисов А. М., Разгулин А. В. Обыкновенные дифференциальные уравнения. М.: МГУ, 2009. 114 с.
- Бицадзе А. В. Уравнения математической физики. М.: Наука, 1976. 296 с.
- Тихонов А. Н., Самарский А. А. У равнения математической физики. М.: Наука, 1977. 736 с.
- Полянин А. Д. Справочник по линейным уравнениям математической физики. М.: Физматлит, 2001. 576 с.
- Краснов М. Л. Интегральные уравнения. Введение в теорию. М.: Наука, 1975. 304 с.


