Критерии устранимых множеств для гармонических функций из соболевских пространств l1 p,w
Автор: Шлык Владимир Алексеевич
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Математика и механика к 75-летию проф. В.М. Миклюкова. Часть I
Статья в выпуске: 2 т.22, 2019 года.
Бесплатный доступ
В работе установлены точные функциональные и емкостные характеристики устранимых множеств для гармонических функций на открытом ограниченном множестве ⊂ 𝑅𝑛, ≥ 2, из весового пространства 𝐿1 𝑝,𝑤(𝐺) с весом 𝑤, удовлетворяющим 𝐴𝑝-условию Макенхаупта, > 1. Доказательство основных результатов базируется на теории распределений по Л. Шварцу и использует свойства экстремальных функций для емкости компакта.
Соболевские пространства, гармонические функции, распределение шварца, емкость множества
Короткий адрес: https://sciup.org/149129859
IDR: 149129859 | УДК: 517.51 | DOI: 10.15688/mpcm.jvolsu.2019.2.4
Текст научной статьи Критерии устранимых множеств для гармонических функций из соболевских пространств l1 p,w
DOI:
В [16] Л. Альфорс и А. Бейрлинг заложили основы теории устранимых множеств для конформных отображений в комплексной плоскости.
В этом направлении, как на плоскости, так и в пространстве, были проведены многочисленные исследования. Не претендуя на полноту, упомянем здесь работы Б. Шабата [15], В. Миклюкова [13], Ю. Вяйсяля [23], А. Копылова [11], В. Асеева и А. Сычева [1], С. Водопьянова и В. Гольдштейна [3], Ю. Дымченко и В. Шлыка [6].
Особо отметим статью Л. Хедберга [19], в которой он, используя распределения по Л. Шварцу, получил точные функциональные и емкостные характеристики устранимых особенностей для классов гармонических функций HDP(G) , FDP(G) .
Ниже, применяя построения Л. Хедберга, мы находим аналогичные характеристики устранимых множеств в классе H DP, W (G) гармонических функций. Кроме того, ° 1 устанавливаем достаточные условия плотности класса C0°(G) в классе L 7W (R n ) .
Отметим, что для класса FDP, W , являющегося обобщением класса FDP, критерии устранимых множеств получены в [5].
1. Терминология и обозначения
Далее G — открытое множество в п -мерном евклидовом пространстве Rn, п > 2 , С к — к -мерная мера Лебега; A P — класс локально интегрируемых функций w : R n ^ ^ (0, + то ) , удовлетворяющих условию Макенхаупта [20]
р - 1
sup i Q i
j wdx
Q
< то ,
Q
где супремум берется по всем координатным кубам Q С Rn , | Q | = G n (Q) , p,q E E (1 , + то ) , р + 1 = 1 .
Вес w 1- обозначим через w и заметим, что ввиду (1) w E А ч . Для весовой функции w E А р обозначим через L pw (G) класс функций и : G ^ ( -то , + то ) , локально интегрируемых в G , имеющих в G обобщенные частные производные и таких, что
У |V u | P wdx < то .
G
В L p, w (G) введем норму
1Ы1Ч™ (G) =
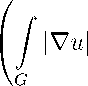
P wdx
р
в котором функции из L pw (G) , отличающиеся друг от друга на постоянную на каждой компоненте связности множества G С п -почти везде, отождествляются. Как известно (см. [21, Theorems 4.4.4, 4.4.6], где класс L p, w (G) имеет обозначение BL ^"1 (G) ), пространство L p w (G) в норме || • ll^ i ^( g ) является полным и C “ (G) является плотным в указанной норме для L p w (G) .
Через HDP,W (G) , следуя Л. Хедбергу, обозначим класс всех гармонических в G функций из L p, w (G) .
Компакт Е С G назовем устранимым для HDP,W (G) , если каждую функцию и E E HDP,W (G \ Е ) можно продолжить до функции из HDP,W (G) .
Через Ер к (G) обозначим класс всех вектор-функций и = (и 1 ,... ,и к ) , для которых
| u | £ P ( G ) =
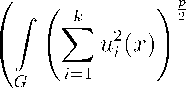
< то .
В случае к = 1 положим C P (G) = Ср (G) .
Запись F обозначает замыкание множества F С Rn в топологии Кп.
Положим для г > 0 B(x,r) = { у E Rn : | у - x | < г } . Носителем supp/ непрерывной в G функции /(x) назовем замыкание в G множества тех x , для которых / (x) = 0 . C 0 ” (R n ) и C ” (G) — совокупность бесконечно дифференцируемых функций в Rn с компактными носителями соответственно в Rn и G .
. о 1
Замыкание C ” (G) по норме L^ (G) обозначим через L pw (G) . В дальнейшем мы будем использовать один результат Фейбса, Кенига, Серапиони [12, теорема 1.3]:
Если Q — ограниченное открытое множество в Rn, то существует положительная постоянная C такая, что для всех п Е C0°(Q) верна оценка j [ulqwdx < C j |Vn|qwdx.
Q
Q
Для компакта К С Rn его (q, w) -емкость относительно Q определим как
Cq,w(К) = inf j |Vg|qWdx, Q где инфимум берется по всем функциям д Е C0°(Q) таким, что д = 1 в окрестности компакта К, где Q — фиксированное ограниченное открытое множество и К С Q. Ниже такие функции назовем допустимыми для Cq<„ (К).
о 1
Функцию п 0 Е Lqi b (Q) назовем экстремальной для Cq ^ (К ) , если она является о 1
пределом в Lqt y (Q) последовательности допустимых функций для Cq^ (К ) и C q ,„ (К) = = J |V u o | q Wdx (o существовании п 0 см. лемму 2).
Q о1 о1
Функцию К Е Lo„(Q) назовем пробной для Cq.6(К), если К = lim пт в Lo„(Q), q, , т^” q, где пт Е C”(Q) и пт = 0 в окрестности компакта К.
о 1
Замечание 1. Если п Е Lqty (G), то, положив п = 0 на Rn \ G, нетрудно заметить, что о1, п Е Lq,^ (R").
Замечание 2. Равенство C q< „ (К) = 0 не зависит от выбора ограниченного открытого множества Q D К . Действительно, пусть C qvw (К ) = 0 относительно Q D К и пусть Q 1 — еще одно открытое ограниченное множество в Rn, К С Q 1 . Рассмотрим неотрицательную функцию К Е C ” (Q П Q 1 ) П C ” (R n ) , где К = 1 в окрестности К и К = 0 на R n \ Q 2 , Q 2 С Q П Q 1 , К С Q 2 (построение такой функции К можно найти в [4, тео- о 1
рема 2.6]). Если пт Е Lqqi(Q) — допустимая для Cq,.„(К) и J |Vnm|qwdx ^ Cq при т ^ то, то К • птЕ Lq,tD(Q П Q1) — допустимая функция для Cq,lb(К) в Q П Q1. В силу (2) j |V(Кnm)|qwdx = j lhVnm + п^К^wdx< QnQ1 QnQ1 < 2qmax |К|q• o(1) + 2qmax |V^qj |пт|qWdx< const • o(1),m ^ to. QnQ1 Следовательно, Cq^(К) = 0 относительно Q П Q1. В силу монотонности Cq^(К) = 0 относительно Q1. Для произвольного множества F C Rn положим Cq<w (F) = 0, если для каждого компакта К C F найдется открытое ограниченное множество Q D К такое, что Cqvw (К) = 0 относительно Q. Пусть T : / ^ К * / — сингулярный интегральный оператор свертки с ядром К, удовлетворяющим следующим стандартным условиям: 1. для преобразования Фурье К ядра К имеем оценку \\К||го< C; 2. |К(х)| < ^; 3. |К(х) - К(х - y)|< ^у для |y| < |2. Здесь C — некоторая постоянная. Известен результат Р. Койфмана и К. Феффермана [18, theorem 3], более подробно см. [21, theorem 5.2.5]: если W Е Ач и /W 1 Е Т?(R1), то I ITf (х)|чгДх< Cqj* |/(х)|чwdx, R" R" где Cq — положительная постоянная, которая зависит только от q,n,w. Если /(х)гч е Сч(G) то в качестве / в (3) нужно рассмотреть функцию, продолженную нулем на Rn \ G. Неравенство (3) при w = 1 было первоначально установлено Кальдероном и Зиг мундом в [17] для ядер К = К^ д2 п> 2; для п = 2 К = К'; = —z— dxidxj д2 / 1 = дх^дх; VITF2/, где |х|= 1(Х1,'",Хп)|> 0 и (-log |х|), где |х| = I(х1, х2)| > 0. Из определения К'; следует, что К ■ = К'з F (х) |х|п где F(х) — ограниченная однородная функция степени 0, то есть F(кх) = F(х) для всех к > 0 и |х| > 0. Доказательство условия 1 для ядер К вида (4) приведено в [14, п. 4.3 гл. II, с. 53]. Очевидно, что (4) влечет условие 2. Условие 3 для К^; следует непосредственно из применения формулы Тейлора в точке х.
2. Вспомогательные утверждения ° 1 Лемма 1. Любой непрерывный линейный функционал на Ьч,,Й(G) можно представить в виде F(“) = /(Ё Ч' tl^ Дс где w ч g е F^G) и g = (gi,..., gn). Кроме того, \\F | < ||ги ч g\C"(G) ■ Доказательство. Очевидно, что правая часть (5) является линейным функционалом ° 1 на Lq,™ (G)и 1 p I f C«)l < I |g| • |Vu| dx = I |g|w чwч |Vu| dx< I j IgIPwdx j ||u|Li -(g). G G Gg / ° 1 Отсюда (5) — ограниченный линейный функционал на Lq™ (G). °1 Обратно, пусть F(и) — некоторый ограниченный линейный функционал на Lq™(G). ° 1/\ 1 Сопоставим вектору Vu, где и Е Lq,™(G), набор х = wчVu из Gq(G). Так как простран-°1 ство Lq™(G) полно (как замкнутое подпространство полного пространства L^™(G)), то °1 область значений оператора V : Lq™(G) ^ ^(G) является замкнутым подпространством пространства C^(G). Определим функционал Ф(х) = F(и) для любого вектора х Е Cn(G), представимого в виде WчVu. Тогда ||Ф| = IF|| и по теореме Хана-Банаха Ф может быть распространен до линейного функционала на ^^(G) с сохранением нор-п мы. В силу линейности Ф(х) можно записать в виде ^2 Фг(хг), где Фг(хг) — линейный г=1 функционал на Gq(G) и х = (х1,..., хп). Отсюда по теореме Рисса Ф(х) = dx, где g = (g1,...,gn) — некоторая функция из Gp,(G). Это дает представление F(и) в виде F(u) = - _ I du g^wf~ дхг dx, где g = (g1,...,gn) = (g1,..., gn)iu ч, и, значит, w ч g е Gp,(G). Тем самым лемма доказана. Обозначим через {-, •) скалярное произведение в Rn. Лемма 2. Если К — компакт в ограниченном открытом множестве G С Rn, то °1 Cq™ (К) < то и существует экстремальная функция и0Е Lq^ (G) для Gj,™ (К) (относительно G), удовлетворяющая следующему вариационному условию: J |Vuo|q-2(Vuq, Vh^ xudx = 0, (6) G где h — произвольная пробная функция для Cq^.™ (К). Доказательство. Известно (см. [8, лемма 1], где все w,p нужно заменить на гх,д), что (q, г)-емкость конденсатора (F0,F1,G) удовлетворяет неравенству Cq<a(F0,F1,G) < < то. Положим Fo= dG, F1 = К. Из определения Cq,™(К) следует, что Cq,™(К) < < Cq™(F0,F1,G). Это дает нужную оценку Cq,™(К) < то. Существование экстремальной функции и соотношение, аналогичное (6), для емкости Cqy(F0,F1,G), получено в [8, теоремы 1,2] (см. также [24]). Для Cq,1i)(К) доказательство повторяет доказательства теорем 1 и 2 из [8] и поэтому его здесь опускаем. Замечание 3. Применяя срезки вида min(1,h) и max(G,h) к допустимым функциям h в определении С q^ (К) и затем аппроксимируя эти срезки гладкими функциями, можно показать, что экстремальная функция uq в лемме 2 удовлетворяет условию G < uq< 1 на G. Лемма 3. Пусть К1и К2— компакты в ограниченном открытом множестве Q и такие, что С q^(К1) = С^(К2) = G. Тогда С q^(К1U К2) = G. Доказательство. Пусть - > G, иг — допустимая функция для Су^(Кг) относительно Q и У |Vuj|9tudx < -, г = 1, 2. Q Тогда и1 + и2 > 1 на К1 U К2 и u1 + u2 G Су0 (Q). Как известно [21, theorem 4.1.4], срезка v = min(1,u1 + u2) G LX(Q) и J |Vv|qwdx < J|V(u1 + u2)|qwdx, v = 1 в ’ Q Q окрестности К1 иК2, supp v лежит в Q. Проводя стандартное усреднение с переменным шагом относительно Q [6, теорема 5], найдем допустимую функцию v1 для Сч<ш(К1 иК2) относительно Q, такую, что J |Vv1|qtud^ = J |Vv|7xbdx + о(1), где о(1) ^ G при - ^ G. Q Q Тогда Сч<й (К1U К2 ) < У |Vvi|yLdx< 2q Q + о(Ц что и завершает доказательство леммы.
3. Критерии устранимых множеств для HDp,w(G) Теорема 1. Пусть Е — компакт в ограниченном открытом множестве G С Rn. Для того чтобы компакт Е был устранимым множеством для III)"-"' (G), необходимо и ° i достаточно, чтобы СQ0(G \Е) было плотным в L^ (G). Доказательство. Необходимость. Пусть Е — устранимое множество для НВР<Ш (G) °1 и пусть С^^ \ Е) не является плотным в L^(G). Если £„(Е) > G, то С^^ \ Е) °1 заведомо не является плотным в Lq^(G) (см. доказательство условия достаточности в теореме). Это позволяет считать Е всюду разрывным компактом в G. Действительно, пусть Х1 — семейство всех (п—1)-мерных гиперплоскостей, ортогональных координатной ж1-оси. Индексируем каждую гиперплоскость Н G Х1 индексом а1, где а1 — точка пересечения этой гиперплоскости с ж1-осью. Положим т = {а1 : Еп-1(На1 П Е) > G}. В силу Еп(Е) > G имеем по теореме Фу-бини оценку ^1(т) > G. Пусть т‘ — компакт в т такой, что ^1(т‘) > G. Если т‘ — всюду разрывный компакт, то положим т1 = т‘. В противном случае т‘ содержит невырожденный отрезок [с, d] и положим тогда в качестве т1 С [с, d] канторово всюду разрывное множество положительной длины. Положим Е1 = ( и наХ \ атетт / П Е. Тогда ^„(Е1) > G. Пусть теперь (п — 1)-мерная гиперплоскость ортогональна координатной ж2-оси и а2 — точка пересечения этой гиперплоскости с осью ж2. Положим На2 = Н. Заменяя в приведенных выше рассуждениях Е на Е1, координатную ось х1 на х2-ось, гиперплоскости На1 на На2, получим всюду разрывный компакт т2такой, что т2С {а2 : En-1(Ha2 П П Е1) > 0}. Положим Е2= I U Ha2 I П Е1. По построению £П(Е2) > 0. \а2ЕТ2 / Продолжая этот процесс дальше, получим последовательность Е1 D Е2D ... D D Еп, где £П(ЕП) > 0 и ортогональная проекция компакта Еп на каждую х^-ось, г = = 1, 2,..., п, есть всюду разрывный компакт положительной длины. Компакт Еп также ° 1 будет устранимым для Н Dp,w (G) и С“ (G \ Еп) не является плотным в L7t5(G). Поэтому ниже считаем, что Е — всюду разрывный компакт в случае Еп(Е) > 0. °1 °1 Тогда существует элемент х0 £ Lq^ (G \ Е) такой, что расстояние между х0 и L7^ (G) положительно. В силу известной леммы об аннуляторе [10, с. 180] существует ненулевое °1 распределение Т на C“(G) с supp Т С Е, непрерывное на Lq,^ (G). Введем распределение S = Т * |x|2-n. Тогда для ф £ C0^(G) справедливо равенство (см. [2, с. 82]) (AS, ф) = С(Т, ф), где постоянная С = 0. Поскольку (Т, ф) = 0 для всех ф £ Cq°(G \ Е), то по одной из теорем Л. Шварца [22, с. 136] обобщенная гармоническая функция S в G \ Е будет гармонической на G\Е в обычном смысле. С другой стороны, поскольку Т — ненулевое распределение на C0°(G), S не является гармонической функцией на G. „ dS _i „ „ Покажем, что ——го ч £ £P(G) для всех з = 1, 2,... ,п. В силу леммы 1 9xj Т как в виде ° 1 линейный непрерывный функционал на L^ (G) можно записать для ф £ Q^G) (Т, ф) = J dx. G Это дает равенство В силу (3) Отсюда (и , ф )=-S^ -1 д 2 / г ч ;—(ф * UXj их г (и • ф) - G |x|2-n) д2 ^г3x<j Зхг (ф * |х|2 n)^ dx. < С||w 1ф|£ч(G). £ч (G) < С||w 5y^£P(G)^W5 ф||£ч^). Введем линейный ограниченный функционал на G0°(G) Ф(у) = / dS \ = Г (^ д2 (ф * |х|2 n)^ dx, V 3xj, ф) 7 ^^ 9г 3xj dxi где х = w ч ф £ Eq(G), ф £ G^(G'). По теореме Хана-Банаха в силу (7) продолжим Ф(у) на Cq(G) до линейного ограниченного функционала с сохранением нормы. Из общего вида линейного ограниченного функционала на С1 (G) [9, теорема 6.2.1] dS -1 „ получим аналогично доказательству леммы 1, что ——w ч Е CP(GY Иначе говоря, 0Жj г ;- i = 1, 2,... ,п. —— wdж < то, J джj G Это влечет S Е L^,w (G). Выше было отмечено, что S Е HDP,W (G \ Е). Покажем, что S не продолжается до функции S Е HDP,W(G). Действительно, пусть S Е HDP,W(G) — продолжение S и Еп(Е) > 0. Напомним, что Е — всюду разрывный компакт. Как известно [21, Theorem 4.1.3, Corollary 4.3.3], LP,W(G) = ACLP,W(G), где ACLP,W(G) — класс функций u, абсолютно непрерывных в G на Сп-1-почти всех отрезках, параллельных координатной ж^-оси, г = 1, 2, ...,п, 1 wрVu Е E^G). Отсюда для С„-почти всех ж0 Е Е S(ж0) = S(ж0) = lim S(ж), где х^хо ж Е G \ Е, ж ^ ж0 вдоль прямой, проходящей через точку ж0 параллельно ж^-оси, г = 1, 2,..., п. Это влечет S = S Еп-почти везде на G, и, значит, 0 = (AS, ф) = (AS, ф) на C^ (G). Тем самым, S — гармоническая функция на G, что противоречит определению распределения Т. В случае СП(Е) = 0 те же рассуждения дают противоречие с определением Т. Значит, Е не является устранимым для HDP,W (G). Из полученного противоречия следует, ° 1 что C0”(G \ Е) является плотным в L1W(G). ° 1 Достаточность. Пусть C0”(G\Е) плотно в L1W(G). Покажем сначала, что En(Е) = = 0. Действительно, предположим, что ЕП(Е) > 0. Выберем открытые множества Q1, Q2 такими, что Е С Q1 С Q1 С Q2С Q2С G. Пусть v(ж) Е C0^(Rn), v = 1 на Q1 и °1 supp v С Q2. Тогда v Е C“(G). В силу плотности C“ (G \Е) в L1W(G) найдется по° 1 следовательность vk Е C“(G \Е), для которой lim vk = v в L„ W (G). Положив в (2) k^^ 11 u = vk — v, Q = G, получим vwч I1 ^ж = 0. lim |vk — vl1 wdж = lim |vk гоч — k^^ GG В силу известного свойства С1(G) найдется подпоследовательность vkl такая, что vklioч ^ 1 ^ vklioч С„-почти везде на Е. Это противоречит тому, что v = 1 на Е, vkl = 0 на Е для всех I > 1. Следовательно, СП(Е) = 0. Пусть теперь u — произвольная функция из HDP<W(G \ Е) и ф Е C0^(G \ Е). Из формулы Грина имеем J(Vu, Vф) dж G j фAu dж = 0. G\E °1 Поскольку ЕП(Е) = 0 и C0”(G \ Е) плотно в L1ilk(G), то У uAф dж = G J(Vu, Vф) dж = 0. G По одной из теорем Л. Шварца [22, с. 136] п — гармоническая функция в G и поэтому принадлежит Н Dp,w (G), что и завершает доказательство теоремы 1. Теорема 2. Пусть G — открытое ограниченное множество в Rn и Е — компакт в G. Е — устранимое множество для HD'P<W(G) тогда и только тогда, когда C q,W(Е) = 0 относительно G. Доказательство. Необходимость. Пусть Е — устранимое множество для HD1P,'W (G) и предположим, что Cq,W (Е) > 0 относительно G. Пусть п0 — экстремальная функция для ° 1 Cq,W(Е) из леммы 2. Рассмотрим соответствующий линейный функционал на Lq,W(G): L(u) = I |Vu0|q-2(Vu0, Vm) wdx. G В силу леммы 2 L(m0) = Cq,W(Е) > 0, L(m) = 0 на C0^(G \ Е), 1 p |L(m)| < I I |Vu0|qwdx \ G ° 1 Другими словами, L(m) — ограниченный ненулевой линейный функционал на LqiW(G). Тем самым функционал L(n) порождает ненулевое распределение Т с носителем на Е. Проводя дальше рассуждения, аналогичные доказательству условия необходимости в теореме 1, построим гармоническую функцию v, которая не продолжается до гармонической функции на G. Следовательно, Cq,W(Е) = 0. Достаточность. В силу теоремы 1 достаточно показать, что каждую функцию °1 Ф G C“(G) можно аппроксимировать в Lq,W(G) функциями из C0°(G \Е). Зададим е > 0 и найдем допустимую функцию v0 G C0^(G) такую, что v0 = 1 в окрестности Е и J |Vv0|qtudx < е. Тогда м0= ф(1 — v0) G C0°(G \ Е) и G j |V(^v0)|quodx = I |фVv0 + v0V^|quodx < G G <2q max |ф|q• е + 2qmax |Vф|qI |v0|qtudx< const • E. G в силу оценки (2). Следовательно, J |V(v — u0)|qtudx< const • е, что влечет плотность C0°(G \ Е) в G °1 классе Lq W(G). По теореме 1 компакт Е — устранимое множество для HDP,W (G). Следствие 1. Пусть G — ограниченное открытое множество в Rn и Е — компакт в G. Если Е — устранимое множество для HDP,W (G), то Е — устранимое множество для НПР,-Ш (G1), где G1 — произвольное открытое множество в Rn. Из леммы 3 получим еще одно утверждение. Следствие 2. Пусть G — ограниченное открытое множество в Rn и Е — компакт в G. Е — устранимое множество для H Dp,w(G) тогда и только тогда, когда для каждой точки х Е Е существует замкнутая окрестность В (х,г) такая, что В(х, г) П Е — устранимое множество для HDP,W(G). Ниже каждую функцию и Е C0°(G) положим равной 0 вне G. Теорема 3. Пусть G — открытое множество в Rn. Если C^(Rn\G) = 0, то C^(G) °1 плотно в Lyjt5(R . Доказательство. Пусть C^ (Rn \G) = 0. Тогда достаточно установить аппроксимацию °1 каждой функции ф Е C^(Rn) функциями из ф Е C0^(G) в Ly,^(Rn). Для заданной функции ф Е C0°(Rn) и е > 0 найдем ограниченное открытое множество Q, для которого supp ф С Q. Положим Е = (supp ф) П (Rn \ G). Из равенства Cyvw (Rn \ G) = 0 следует, что Cyvw (Е) = 0. Тогда найдется допустимая функция т0 для Cy У |V(ф — u0)|ytudx = У |V(ф — uo)|yixdx< const • е. R" Q Тем самым теорема доказана.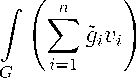
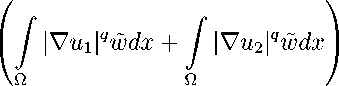
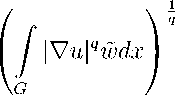
Список литературы Критерии устранимых множеств для гармонических функций из соболевских пространств l1 p,w
- Асеев, В. В. О множествах, устранимых для пространственных квазиконформных отображений / В. В. Асеев, А. В. Сычев // Сиб. мат. журн. - 1974. - Т. 15, № 6. - C. 1213-1227.
- Владимиров, В. С. Обобщенные функции в математической физике / В. С. Владимиров. - М.: Наука, 1976. - 280 c.
- Водопьянов, С. К. Критерий устранимости множеств для пространств 𝐿1, квазиконформных и квазиизометрических отображений / С. К. Водопьянов, В. М. Гольдштейн // Сиб. мат. журн. - 1977. - Т. 18, № 1. - C. 49-68.
- Гольдштейн, В. М. Введение в теорию функций с обобщенными производными и квазиконформные отображения / В. М. Гольдштейн, Ю. Г. Решетняк. - М.: Наука, 1983. - 284 c.
- Демшин, И. Н. Критерии устранимых множеств для весовых пространств гармонических функций / И. Н. Демшин, В. А. Шлык // Зап. науч. семинара ПОМИ. - 2002. - Т. 286. - C. 62-73.
- Дымченко, Ю. В. Достаточность семейства ломаных в методе модулей и устранимые множества / Ю. В. Дымченко, В. А. Шлык // Сиб. мат. журн. - 2010. - Т. 51, № 6. - C. 1298-1315.
- Дымченко, Ю. В. Об одной задаче Дубинина для емкости конденсатора с конечным числом пластин / Ю. В. Дымченко, В. А. Шлык // Мат. заметки. - 2018. - Т. 103, № 6. - C. 841-852.
- Дымченко, Ю. В. Соотношение между весовой емкостью конденсатора и весовым модулем семейства разделяющих поверхностей / Ю. В. Дымченко, В. А. Шлык // Дальневосточный мат. сб. - 1996. - № 2. - C. 72-80.
- Канторович, Л. В. Функциональный анализ / Л. В. Канторович, Г. П. Акилов. - М.: Наука, 1977. - 744 c.
- Колмогоров, А. Н. Элементы теории функций и функционального анализа / А. Н. Колмогоров, С. В. Фомин. - М.: Наука, 1989. - 544 c.
- Копылов, А. П. Об устранимости плоских множеств в классе трехмерных квазиконформных отображений / А. П. Копылов // Метрические вопросы теории функций и отображений. - 1964. - № 1. - C. 21-23.
- Мазья, В. Г. Классы областей, мер и емкостей в теории пространств дифференцируемых функций / В. Г. Мазья // Современные проблемы. Фундаментальные направления. - 1988. - Т. 26. - C. 159-228.
- Миклюков, В. М. Об устранимых особенностях квазиконформных отображений в пространстве / В. М. Миклюков // Докл. АН СССР. - 1969. - Т. 188, № 3. - C. 525-527.
- Стейн, И. Сингулярные интегралы и дифференциальные свойства функций / И. Стейн. - М.: Мир, 1973. - 342 c.
- Шабат, Б. В. К теории квазиконформных отображений в пространстве / Б. В. Шабат // Докл. АН СССР. - 1960. - Т. 132, № 5. - C. 1045-1048.
- Ahlfors, L. V. Conformal invariants and functions-theoretic null-sets / L. V. Ahlfors, A. Beurling // Acta Math. - 1950. - Vol. 83, № 1-2. - P. 101-129.
- Calderon, A. P. On the existence of certain singular integrals / A. P. Calderon, A. Zygmund // Acta Math. - 1952. - Vol. 88. - P. 85-139.
- Coifman, R. R. Weighted norm inequalities integrals / R. R. Coifman, C. Fefferman // Studia Math. - 1974. - Vol. 51. - P. 241-250.
- Hedberg, L. I. Removable singularities and condenser capacities / L. I. Hedberg // Arkiv. Math. - 1974. - Vol. 12, № 2. - P. 101-129.
- Muckenhoupt, B. The equivalence of two conditions for weight functions / B. Muckenhoupt // Studia Math. - 1974. - Vol. 49. - P. 101-106.
- Ohtsuka, M. Extremal length and precise functions / M. Ohtsuka // Gakuto international Series. - 2003. - Vol. 19. - P. 1-343.
- Schwartz, L. Therie des distributions / L. Schwartz. - Paris: Hermann, 1950. - Vol. 1. - 148 p.
- Va¨isa¨la¨, J. Removable sets for quasiconformal mappings / J. Va¨isa¨la¨ // J. Math. Mech. - 1969. - Vol. 19, № 1. - P. 49-51.
- Ziemer, W. P. Extremal length and conformal capacity / W. P. Ziemer // Trans. Amer. Math Soc. - 1967. - Vol. 126, № 3. - P. 460-473.


