Квазисоболевы пространства l pm

Ω⊂Rn –                                    C∞ .-

W_p^m (Ω), m ∈ {0} ∪ N , p ∈ [1,+∞) ;

Wpm (Ω) = L2 (Ω) –                       [1].                          [1]-

1    m -t 1

лева: при всех me N, t = 0,1,...,m-1, p,qe [1, +^) таких, что —I--< — < 1, имеют место pnq плотные и непрерывные вложения wpm (Q) с Wq (Q)(1)

Нашей задачей является распространение данного результата на квазисоболевы пространства последовательностей k}: Я^Ы k=1^> p∈(0,+∞) , m∈ R, {λk} –-

, lim λk =+∞., k→∞

,                          [2],-

..

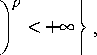
t ^mp = ^ X = { X

1..

℘ –                              (                 ).

(℘, _p ⋅ ),                      _p ⋅ : ℘→ R -

:

(iii) ∀ x , y ∈ ℘ _px + y ≤const

x + y pp

,                  const ≥ 1                         x ,

y .

(℘, _p ⋅ )                                             -

℘ .                     { x_k } ⊂ ℘                           x ∈ ℘,

Краткие сообщения

1 1П    V _ V -- ЧТЛТ /TAQL'T Д^Х/ТТОЛГ ООТГТЛТ'Т-ТТЗ'Д'Т'Т- 'T'OTZ*  Inn V — Y l/'li"' ГТГХ ТТ/Л R‘ЛТД2'TTR T T/XR'm UOОТТГХ! ^ТР(Г lim p Xk  X — 0 . CzlUl фс1К1 иуд CM odllHCblodlb IdK.  lim xk — X . 110UJlCД0.DdiCJlbгЮUib ildlblbdClOi k ^~ p                                           k ^~ фундаментальной, если lim (xk - xr) — 0. k, r ^~

Пространство p называется квазибанаховым, если любая фундаментальная последовательность в нем сходится к некоторой точке этого пространства. Отметим сразу, что любое банахово пространство является квазибанаховым, а обратное, вообще говоря, неверно.

Пример 1. Пространства £ m - квазибанаховы при всех p е (0, +~), однако они банаховы только при p е [1, +^ ).

Теорема 1. Квазисоболевьi пространства £ ^m _p , т е R , p е R ₊ , являются квазибанаховыми.

Приведем набросок доказательства. На, очевидно, линейном пространстве £^т_р построим функцию p || • 11: £ т ^ R по формуле

у

( т     \Р ) p ти — z[ATiXki) k k,k 7 7

Эта функция, очевидно, удовлетворяет аксиомам (i) и (ii) квазинормы. Рассмотрим вектор y — { ^_k ² x_k }е £ _p , поэтому p • || удовлетворяет и аксиоме (iii), причем const — 2^{/ p} при p е (0,1), и const — 1 пр и p е [1, +^) [2].

Рассмотрим фундаментальную в £ ^т _р последовательность { x_£ }. Ее координатные последовательности { x^k } _k—1, k е N , фундаментальны и в силу полноты R сходятся к x^k . Полученный предел x — { x^k } и будет искомым [2].

Аль -Делфи Д. К.

Квазисоболевы пространства £ mm

Теорема 3. При всех p е R ₊ и m е R квазиоператор Лапласа Л: £ mp ⁺² ^ £ mp - топлинейный .

Доказательство . Непрерывноеть оператора Л очевидна в силу

m.,-1     kpVpl ^x II = ZI 2+1kkil = m+>11.

k k = 1 ^{k           7} )

Построим обратный оператор Л^-1 x = { 2 - xk } ( квазиоператор Грина) . Очевидно, Л^-1Л x = x при всех x е £ *p⁺² и ЛЛ^-1 x = x при всех x е £ *p . Далее,

, -            ” f m+2 , kp p m+pl^x II = ZI v "'ixkil     = mp\\x\\.

k k=1k^ 7

.Соболевых пространств £ ^m _p очевидно.

свою

.