Линейные параметрические стохастические системы нейтрального типа с кратными запаздываниями

Как известно, в последние годы значительный интерес вызывают проблемы, связанные с анализом явлений, которые описываются функционально-дифференциальными уравнениями (ФДУ) и их частными формами, такими как ДУ с запаздыванием, ДУ нейтрального типа, иптегро-дифферепциальпые уравнения и др. [1-4]. Свидетельством этого служит постоянно увеличивающийся поток публикаций по данной тематике.

В настоящее время существует только несколько областей исследования ФДУ, где ведутся интенсивные научных разработки. Среди них качественный анализ существования и устойчивости решений ФДУ; прямое количественное исследование линейных систем, в первую очередь, па основе применения классического метода шагов; использование процедур усреднения ДУ с учетом малости запаздывания; различные чис-

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 11-01-96024).

лепные интеграторы и другие методики для получения частных решений задач [4-6] и т.д.

В процессе развития методов анализа указанных систем, ставших уже классическими, возник интерес к стохастическим ФДУ разных типов [1,4,7-9]. Но исследование таких систем вызывает значительные трудности.

Наша схема анализа некоторых классов систем стохастических дифференциальных уравнений (СДУ) с запаздыванием [10-13] базируется па комбинации метода шагов и расширении фазового пространства (МШРФП) и позволяет строить процедуры исследования различных форм ФДУ с одной точки зрения. При этом в большинстве вариантов схемы ошибка метода отсутствует. Кроме того, исчезают многие проблемы, возникающие при реализации процедур прямого численного интегрирования ДУ с запаздыванием. В данной работе мы представляем детали этой схемы для анализа систем линейных неавтономных СДУ нейтрального типа с кратными постоянными запаздываниями, которые возмущаются аддитивными и мультипликативными случайными шумами. Применение этой схемы демонстрируется па примерах. Инструментом расчетов являлся пакет компьютерной алгебры (ПКА) Mathematica [14].

1. Постановка задачи и метод исследования

Рассмотрим последовательность систем линейных параметрических СДУ Стратоновича [15] нейтрального типа с кратными постоянными запаздываниями следующего вида ( r = О, 1, ..., v, при r = 0 без запаздывания):

r

X ( t ) = P r ( t ) + £ Pr,r- ( t ) X ( t - (t ) +

£ =1

+ ^£ Qr,r-£ ( t ) X ( t - (t ) + £ =0

+ [ Ur ( t ) + ^£ Vr,r-£ ( t ) : X (t - (t )] o W ( t ) , £ =0

t>tr = 1 0 + r ■ T ; X ( t o) = X *,     (1)

где t ф 1 0 - время; t = const >  0: X ( t ) = {Xi ( t ) }. i = 1.2 n. - фазовьin вектор; X * = {X*}. i = 1, 2, ..., n, - случайный вектор с известными характеристиками; W ( t ) = {Wj ( t ) }, j = 1, 2, ..., m, - вектор независимых случайных функций типа белого шума с единичными иитеисивиостями:

M [ ^W ( t )]=⁰ ,               ₍₂₎

M [ W ( 1 1) V W T( 1 2)] = E ■ 6 ( 1 1 - 1 2)

(W ( t ) - вектор независимых стандартных винеровских процессов); p _r ( t ) = {p_ri ( t ) }, P_r£ ( t ) = {Pr£ij ( t ) }- Qr£ ( t ) = {qr£ij ( t ) }. Ur ( t ) = {u_nk ( t ) }. V_r£ ( t ) = {v_r£ijk ( t ) } - неслучайные векторы и матрицы; i. j = 1. 2   n: k = 1. 2   m: T 11 M - символы траиспоиироваиия и математического ожидания соответственно; E - единичная матрица;

S : Y = {^£ Sijk ^Yj } ’ i = 1n k = l ^m-j =1

Пусть в момент времени 1 0 заданы значения элементов вектора математических ожидании m * = M [ X * ] и матрицы дисперсий

D* = M [{ X * - m * }{ X * - т * }^т] .

Задачей исследования является построение системы обыкновенных дифференциальных уравнений (ОДУ) для компонентов вектора средних т ( t ) = M [ X ( t )] 11 матрицьi дисперсий D ( t ) = M[{ X ( t ) - m ( t )}{ X ( t ) - m ( t )} ^T ] сказового вектора X ( t ) при лтобом t ф 10.

Как и в ряде предыдущих наших работ, для того чтобы получить СДУ без запаздывания, применим метод расширения фазового пространства. Для этого введем следующие обозначения ( q = 0 , 1 , 2 ,...):

X q ( S )= X ( Sq ) , W q ( S ) = W ( Sq ) , A q = ( tq- 1 ,tq ] ,    Z 0 = X 0 , S 0 = W 0 ,   (3)

Z 1 = col( X 0 , X 1) , Z 2 = col( X 0 , X 1 , X 2) ,..., S 1 = col( W 0 , W 1) , S 2 = col( W 0 , W 1 , W 1) ,..., W q (0)= W q— 1( T ) , Y q ^ X q (0) = X q- 1 ( T ) , col( X 0 ,---, X N - 1 , X N ) = {X 01 ,X 02 ,...,X 0 n, ...,X_N 1 ,X n 2 ,...,XNn}^T-

Рассмотрим последовательность полуинтервалов (сегментов) A _q.

0°. На сегменте A0 систему СДУ Стратоновича, решением которой является случайная векторная функция Z 0( s ) = X 0( s ), можно записать в следующем виде (здесь и далее точкой обозначена производная по переменной s):

^X 0^{( s} ) = P 0^{( s} 0) + Q 00^{( s} 0) ^X 0^{( s} )+

+ [ U 0( s 0) + V 00 ( s 0) : X 0( s )] o W 0( s ) - 1°. На сегментах A0 11 A1 систему СДУ для вычисления вектора Z 1( s ) = col( X 0( s ) , X 1( s )) можно представить так:

XX 0^{( s} ) = P 0^{( s} 0) + Q 00^{( s} 0) ^X 0^{( s} )+

+ [ U 0^{( s} 0) + V 00^{( s} 0) ^{: X} 0^{( s} )] ^{o W} 0^{( s} ) ,

^X 1^{( s} ) = ^p 1^{( s} 1) + ^P 10^{( s} 1) ^X 0^{( s} )+

+ Q 10( s 1) X 0( s )+ Q 11( s 1) X 1( s )+

⁺ [ U 1^{( s} 1) ⁺ V 10^{( s} 1) ^{: X} 0^{( s} )+ + V 11( s 1) : X 1( s )] o W 1( s ) .

... ... ... ... ... ... ... ... ...

v°. Рассматривая сегменты A0. A1  A _v совместно, запишем систему СДУ для вычисления вектора Z _v ( s ):

^X 0^{( s} ) = P 0^{( s} 0) + Q 00^{( s} 0) ^X 0^{( s} )+

+ [ U 0( s 0) + V ю( S 0) : X 0( s )] o W 0( s ) , XX 1^{( s} ) = ^p 1^{( s} 1) + P 10 ^{( s} 1) ^X 0^{( s} ) +

+ Q 10^{( s} 1) ^X 0^{( s} ) + Q 11^{( s} 1) ^X 1^{( s} )+

+ [u 1( s 1)+ V 10( S 1) : X 0( s )+ + V 11( s 1) : X 1( s )] o W 1( s ) , ... ... ... ... ... ... ... ... ...

X v ( s ) = P v ( Sv ) + ^£ Pv,v-£ ( Sv ) X v-£ ( s ) + £ =1 v

⁺ ^2 Qv,v-£ ^{( s}v ) ^Xv-£ ^{( s ) +} £ =0

+ [ Uv ( Sv ) + ]T Vv,v-£ ( Sv ) : X v-£ ( s )] o W v ( S ) -£ =0

( v + 1)°. На ссгментах A_o. A i A _V. A _{V +}i уравнения для компонентов случайной векторной функции Z _V +₁( s ) можно записать в следующем виде:

XX 0⁽ s ) — Р 0⁽ s q ) + Q qq ⁽ s q ) X q ⁽ s ) +

+ [ U o( s q ) + V qq ( s q ) : X o( s )] o W o( s ) , X 1⁽ s ) ^— p ₁ ⁽ s 1) + ^P 1Q^{( s} 1) ^X q ⁽ s ) +

+ Q 10^{( s} 1) ^X 0^{( s} ) + Q 11^{( s} 1) ^X 1⁽ s )+

+ [ U 1( s 1) + V 10( s 1) : X o( s )+

+ V 11 ( s 1) : X 1( s )] o W 1 ( s ) ,

V

X V ( s ) — P v ( sv ) + ]T Pv,v-e ( sv ) X v-e ( s ) + £ =1

V

+ У^ Qv,v-£ (s„) Xv-e (s)+ e=q

+ [ U v ( sv ) + ^y V v,v - £ ( sv ) : X v-e ( s )] o W v ( s ) , e =q

^X V +1^{( s} )    p v ^{( s}V + 1) +

V

+    Pv,v-£ (sv+1) X V-e +1(s) + e =1

V

+ У ^Q v,v - £ ^{( s}v +1) ^X v - £ +1^{( s ) +} |^ Uv ^{( s}v +1^{) +} e =q

V

+     VVV-I ⁽ sv +1) ^{: X} V-e +1^{( s} )j ^o^W V +1 ^{( s} ) .

e =q

№. Наконец, на сегментах Aq, A_1; ..., A _V, A _V +_1; ..., A n систему СДУ для вычисления вектора Z n ( s ) можно представить так:

^X 0^{( s} ) ^— Р 0^{( s} 0) + ^Q 00^{( s} 0) ^X 0^{( s} )+

+ [ U o( s о) + V 00( s о) : X o( s )] o W q ( s ) , ^X 1^{( s} ) ^{— p} ₁ ^{( s} 1) + ^P 10^{( s} 1) ^X 0^{( s} ) +

+ ^Q 10^{( s} 1) ^X 0^{( s} ) + ^Q 11^{( s} 1) ^X 1^{( s )+}

+ [ u 1( s 1) + V 10( s 1) : X o( s )+

+ V 11 ( s 1) : X 1( s )] o W 1 ( s ) ,

V

XV (s) — Pv (sv) + У Pv,v-£ (sv) XV-e (s) + e =1

V

+ У Qv,v-e(sv) Xv-e(s)+ e=o

V

+ [ U v ( sv ) + ]T Vv,v-e ( sv ) : X v-e ( s )] o W „ ( s ) , e =o

^XV + 1^{( s} )    p v ^{( s}V + 1) I

V

+    Pv,v-£ (sv +1) Xv-£ +1(s) + e=1

V

+ У ^Qv,v-e ⁽ sv +1) ^Xv-e +1^{( s} ) ¹ |^ ^Uv ⁽ sv +1⁾⁺ e =o

V

+     ^V-v-e ( sv +1) : X v-e +1( s )] o W v +1( s ) .

e =o

X N ( s ) — P v ( s n ) +

V

+    Pv,v-e (sn ) Xn-e (s)+ e=1

V

+ У Qv,v-e ( s n ) X n -e ( s )+ Цл ( s n )+ e =o

V

+ У Vv,v-e ( s n ) : X n -e ( s )] o W n ( s ) . e =o • • •         ■ ■ ■         ■ ■ ■         ■ ■ ■         ■ ■ ■         ■ ■ ■         ■ ■ ■         ■ ■ ■         ■ ■ ■

• 2.    Вывод уравнений для моментов

Теперь построенную выше па основе применяемой схемы цепочку параметрических линейных СДУ без запаздывания можно использовать для получения повой последовательности уравнений - последовательности ОДУ для первых моментов векторов Zq, Z 1; ..., Zn, ••• и Z + — col(Yо, Zо). Z + — col(Yо, Z1)  ZN — col(Yq, ZN). причем mk (s) — M [Zk] = col( mx □, mx 1,..., mXk), m+ (s) — M[ Z+] — col( m*, mk (s)),

Dk ( s ) — M [ Z kk - m k) (Z_k - m^ ] —

DX 0 X 0   DX 0 X 1   ...  DX 0 X k

Dx 1 X 0   DX 1 X 1   ...  DX 1 X k

— ,

...               ...          ...          ...

_ DX k X 0   DX k X 1   ...  DX k X k

D + ( s ) —	' Dk +(11)( s )    . ...              .	..   D k +(12) ( s ) ..              ...
	_ Dk +(21)( s )    .	..   D k +(22) ( s )

D +(11)( s ) —	DY j X 0   DY' j X 0 DY' 0 X 0   DX 0 X 0 _ DY- 0 X 1   DX 1 X 0	DY 0 X 1 DX 0 X 1 DX 1 X 1
Dk +(12)( s ) —	[ DY' 0 X k , DX 0 X k , DX 1 X k ] T
Dk +(21)( s ) —	DY' 0 X k   DX k X 0	DX k X 1
D +(22) ( s ) — [ DXkXk		] ,
k	— 0 , 1 , 2 , ...,N,...

В связи с тем что вектор m k ( s ) и матрица Dk ( s ) являются блоками вектора m +( s ) и матрицы D + ( s ) соответственно, достаточно вычислить только последние, а затем выбрать их необходимые элементы.

Несложно увидеть, что на каждом этапе r (r = 0, 1, ..., N , ...) структура систем СДУ принимает следующую форму:

Z r ( s ) = f r ( Z r ( s ) ,s ) + Gr ( Z r ( s ) , s ) ◦ S r ( s ) , ( 4 )

где

f r = {fri},

Gr = {grik},

n ( r +1)

^fri ^{— f}r 0 i ^{( s} ) ⁺ ^ ^frij ⁽ s ) ' Zrj ⁽ s ) , j =1

n ( r +1)

grik — gr 0 ik ^{( s} ) ⁺

E grj ( s ) • Zr₃ ( s ) ,

j =1

i — 1 , 2 , ..., n ( r +1) , k — 1 , 2 , ..., m ( r + 1) .

Используя компоненты векторов f r и матриц Gr и заменяя в них элементы случайного вектора Zr их возможными значениями, по формулам Стратоновича [15] мы можем вычислить коэффициенты сноса и диффузии ari

n ( r +1) m ( r +1)

— fri + 2 E E j=1   k=1

∂grik ∂zrj

grjk ,

m(r+1) brij —        gnk grjk, k=1

i,j — 1 , 2 , ..., n ( r + 1)

уравнения Фоккера - Планка - Колмогорова для плотности вероятности вектора Z _r ( s ). В свою очередь, па основе этого уравнения может быть построена замкнутая система ОДУ для элементов векторов m _r ( s ) и матрип D_r ( s ) в следующем виде:

m„ ( s ) — M [ a„],

^D rij ^{( s} ) — ^M[⁽ zri   mri ) • ^arj ⁺

^{+ (} zrj   mrj ) • ^ari ⁺ brij ] .   ^X)

К этим уравнениям необходимо добавить начальные условия, форма которых будет такова:

mri (0) — |

mi*, mr-1 ,i (т),

r — 0 , r >  0;

Dr ⁺ (0) —

D*

D*

D*

D*

D + - 1(0) D^

,

Dri2)

Dr22)

, r> 0 ,

(Ю)

D r ⁱ²⁾ —

DY 0 X r - 1 ^{( т} ) DY о X r — i ^{( т} ) DX о X r - 1 ^{( т} )

...

DX- 2 X r — i ^{( т} )

Dr ^{21) —} [ DX r - 1 Y о ^{( т} ) DX r - 1 Y о ^{( т} )

^DX r 1 X 0 ^{( т} ) ... DX r - 1 X r - 2 ^{( т} )] ,

D? 2 — DX r - 1 X r - 1 ( т ) .

• 3.    Примеры

Для демонстрации изложенной методики был осуществлен анализ поведения нескольких стохастических систем различной размерности. Некоторая часть полученных результатов приводится ниже. Все численно-аналитические расчеты были проведены с помощью программ па входном языке пакета Mathematica [14].

В качестве первой исследуемой модели была выбрана система

X(t) — q00 X(t) + [uо + v00 X(t)] W(t), t G (0,т],     m(0) — m*,     D(0) — D*;

^{X (} t ) ^— p 10 ^{X (} t^{— т} ) ⁺ q 10 ^{X (} t^{— т} ) ⁺ q 11 ^{X (} t ⁾⁺

+ [u 1 + v 10 X(t — т) + v 11X(t)] VW(t), t G (т, 2т];

X ( t ) — p 20 X ( t - 2 т ) + p 21 X ( t - т )+

+ q 20 X ( t - 2 т ) + q 21 X ( t - т ) + q 22 X ( t )+

+ [ u 2 + v 20 X ( t — 2 т ) + v 21 X ( t — т )+

+ v22 X (t)] W(t) , t > 2т, где pij, qij, ui, vij - постоянные. На рис.1 и 2 изображено поведение математического ожидания и дисперсии X(t) при следующих значениях параметров:

u 0 — 0,125, v 00 — 0,1, p 10 — 0,25, q 10 — 0,25, q 11 — 1, u 1 — 0,1, v 11 — 0,1, p 20 — 0,25, p 21 — - 0,125, q 20 — 0,25, q 21 — — 0,25, q 22 — —1, u 2 — — 0,125, v 20 — 0,1, v 21 — 0,05, v22 — 0,05,

• ^q 00 ^{: a} ) ^{— 1} , b ) ^{— 2} ,

2.0 0.5 0.0 0.4

v 10 : a) 0,25, b) — 0,125, т — 0.5, 10 — 0, m0 — 2, D0 — 0,25.

1.5

1.0

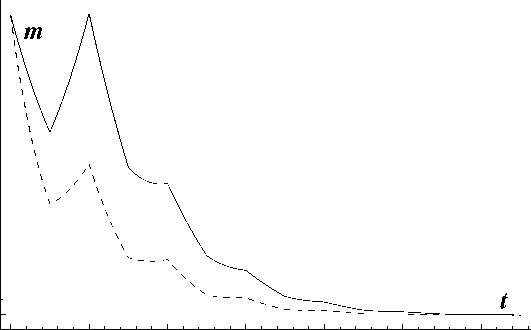
Рис.1

0.0 0

D

0.3

0.1

0.2

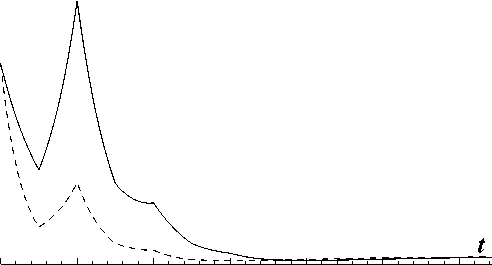
Рис.2

На этих рисунках случаю а) соответствуют непрерывные линии, а Ь) - штриховые.

Заключение

Методика, описанная в данной работе, может быть эффективно реализована па основе любого современного ПКА, такого как Maple или Matlab [6,16], и использована для изучения многих типов систем с последействием как па основе полученных ОДУ для первых моментов, так и с помощью метода статистического моделирования (Монте-Карло) [17] в случае нелинейных систем. В отличие от известных других методов изложенная методика не предполагает предварительного изменения уравнений исследуемого объекта с целью исключения запаздывания. Более того, данная схема позволяет вычислять моментные функции и более высоких порядков.