Local Detectors and Descriptors for Object Class Recognition

Published Online September 2015 in MECS

The field of computer vision has many various applications that basically depend on local feature detection and description. Examples of these applications are object recognition [1], object tracking [2], 3D reconstruction [3] image stitching [4] and visual mapping [5].

A feature detector selects points of interest that have unique content within an image. The key to feature detection is to find features that remain locally invariant so that you can detect them even in the presence of any type of deformations such as rotation, scale, illumination changes. An ideal feature detector should achieve repeatability, distinctiveness, locality, quantity, accuracy, and efficiency [6]. A feature descriptor (extractor) describes the region around each detected feature. Feature descriptors rely on image processing to transform a local pixel neighborhood into a compact vector representation. The resulting feature descriptors are then used for comparison and matching between neighborhoods regardless of any deformations. There are two types of descriptors; patch descriptors and binary descriptors, as will be discussed later. An ideal feature descriptor should be distinct, efficient and invariant to common deformations such as scale, rotation, image noise, and illumination changes. Moreover, the detector and the descriptor should be fast enough in order to be exploited in real-time applications.

The SIFT (Scale Invariant Feature Transform) [7] algorithm is considered the most important feature detector and descriptor and has been widely used in many applications. During the past decade, a lot of algorithms have been proposed with the aim of increasing the speed and efficiency of the feature detection and description process [8-12]. Many comparisons have been established between them [13-16] and between their different implementations [17, 18]. All these comparisons are carried out on a set of images with random structures and the results are reported for every deformation case. In addition, there is no best method for all deformations [15].

An object class recognition application could be faced with all types of deformations. Moreover, some object class recognition applications, such as multi-object tracking applications, deal with different object classes. For example, in a digilog book, many objects of different classes have to be detected and tracked.

The objective of this paper is to investigate the overall performance of the most recent feature detectors and descriptors on a set of images of different classes with all possible deformations. We want to know how detectors and descriptors deal with different image structures.

Our results would be useful by adding more flexibility and hence efficiency to object recognition applications. For single-object recognition, the most suitable (efficient) detector and descriptor could be determined beforehand based on the targeted object class. On the other hand, multi-object applications could be more flexible and efficient. Flexibility could be achieved by detecting the most suitable algorithm for each tracked object class.

Once the current object class is changed during the recognition process, the algorithm used could be automatically replaced by the most suitable one for that class.

The detectors included in the evaluation are SIFT, SUIRF (Speeded-Up Robust Features), ORB (Oriented FAST and Rotated BRIEF), FAST (Features from Accelerated Segment Test) and BRISK (Binary Robust Invariant Scalable Keypoints). The descriptors are SIFT, SURF, ORB, BRISK and BRIEF (Binary Robust Independent Elementary Features).

The organization of the remaining content is as follows: An overview of the algorithms and the related work are presented in section II. Section III presents the evaluation criteria for our evaluation and the data sets used as well as the implementation details. In section IV, the experimental results are discussed. Finally, the conclusion is reported in section V.

• II.    Overview and Related Work

• A.    Local feaure detectors overview

Despite its extreme slowness, the SIFT [7] algorithm has attracted a great attention due to its high efficiency. It detects features using Difference of Gaussians (DoG) which is an approximation of the little costly Laplacian of Gaussian (LoG). It builds a scale-space pyramid of filtered images. Such pyramid consists of a number of layers (octaves) and scales. Each octave is created by half-sampling the original image. Each scale is the result of convolving the corresponding octave with the Gaussian kernel using incremental scaling parameter. Then, adjacent layers are subtracted to produce the DoG pyramid. Features are identified as local maxima of the DoG at each scale. A Local maxima is obtained by comparing each pixel in the pyramid with its 8 neighbors as well as 9 pixels in the next scale and 9 pixels in the previous scales. DoG is sensitive to edges, so the Hessian matrix is used for eliminating this sensitivity. An orientation is assigned to each keypoint to achieve rotation invariance. Gradient magnitudes and directions are calculated for the neighboring pixels. A histogram with 36 bins covering 360 degrees is created. An orientation is obtained from peaks in the histogram.

SURF [8] is a powerful scale and rotation-invariant interest point detector which is faster than SIFT. It approximates LoG with Box Filters for finding scalespace. They are efficiently evaluated very fast using integral images, independently of their size. SURF is based on the determinant of the Hessian matrix which is efficiently calculated using Box filters. A scale-space representation is built from a number of octaves. An octave is a set of images filtered by a double scaled up kernel. Features are detected as local maxima in a 3×3×3 neighborhood in the scale-space. Each keypoint is assigned an orientation by calculating the Haar wavelet responses in horizontal and vertical direction within a circular neighborhood. Such neighborhood is of radius 6s around the interest point, where s is the scale at which the keypoint was detected. The wavelet response can be easily found out using integral images at any scale. They are adequately weighted with a Gaussian kernel. All responses within a sliding orientation window of angle 60 degrees are summed to calculate the dominant orientation.

An extremely fast detector is FAST [11]. It is a corner detection method which is based on examining the image intensity of a circle of 16 pixels centered at a candidate pixel. The pixel is a corner if there is a set of n contiguous pixels in the circle which are all brighter\ darker than intensity plus\minus a predefined threshold. n was chosen to be twelve. A high-speed test was proposed to exclude a large number of non-corners. The test examines only pixels at the four compass directions. At least three of them must achieve the previously mentioned condition in order to realize that the candidate pixel is a corner. Machine learning for a corner detector can be used. The FAST algorithm is run on a set of training images to build a vector of the detected feature points. The vector is subdivided into 3 subsets: darker, similar and brighter. A new Boolean variable is defined which is true if the point is a corner and false otherwise. The ID3 algorithm (decision tree classifier) is used to query each subset using the Boolean variable. The decision tree so created is used for fast detection in other images. Non-maximum Suppression is used to solve the problem of detecting multiple interest points in adjacent locations. The disadvantages of FAST are that it is not robust to high levels of noise and it is dependent on a threshold.

An efficient extension to FAST is the recently proposed ORB [9] detector. It addresses the weaknesses of FAST (rotation and scale invariance). It uses FAST to detect keypoints. Then, it applies the Harris corner detector for quality measure. For scale invariance, it uses scale pyramid to produce multiscale-features like SIFT. For rotation invariance, it computes the intensity weighted centroid moment of the patch with located keypoint at center. The orientation is obtained from the direction of the vector from this corner point to the centroid. To improve the rotation invariance, moments are computed. It is a fast and robust feature detector.

BRISK [12] also extends FAST by searching for maxima not only in the image plane, but also in a 3D scale-space. So, it is a scale-invariant detector. It first creates a scale space pyramid which consists of a number of octaves and intra-octaves. The octaves are formed by half-sampling the original image. Then, it computes FAST score across this scale space. It applies nonmaximal suppression on the pixel level and computes sub-pixel maximum across patch. It computes continuous maximum across scales. Image coordinates from scale space feature point detection are re-interpolated.

• B.    Local feaure descriptors overview

Patch descriptors [7, 8] are based on local histogram of gradients (HOG). They have been successfully used in various applications. They are computationally expansive. Even though SURF speeds up the computation using integral images, this still isn’t fast enough for some applications.

On the other hand, a recent approach is to use binary descriptors [9, 10, 12] which are considered efficient alternatives to their floating-point competitors as they enable faster processing while requiring less memory. This fast processing is because only local intensity comparisons are needed to form a binary string and using the hamming distance as a distance measure between two binary strings. They are especially suited for real time applications and low power devices.

SIFT [7] descriptor is based on the gradient magnitude and orientation computed at the scale of the considered keypoint. A region of size 16×16 around the keypoint is taken. It is divided into 16 sub-regions of size 4×4. For each sub-region, 8-bin orientation histogram is created. Those 16 histograms are concatenated together to form a final descriptor as a 128 dimensional feature vector in length. It is invariant to rotation, scale and illumination changes.

SURF [8] descriptor is a distribution-based descriptor and is also based on Haar wavelet responses. A region around the keypoint (detected in scale s ) of size 20 s is selected and split up into 4×4 sub-regions. For each subregion, horizontal and vertical wavelet responses are calculated and a 4-dimensional feature vector is formed. 16 4-dimensional vectors are combined together to build a descriptor with total 64 dimensions. So, it is faster in computation and matching than SIFT, nevertheless it is still not suitable for real-time applications.

BRIEF [10] descriptor was the first binary descriptor published and is the simplest one. It does not have a precise sampling pattern or an orientation compensation mechanism. It randomly selects pairs of pixels for building the descriptor. There are five methods proposed by the authors for selecting the point pairs. One of them is the Gaussian distribution which achieves the best results. The descriptor simply constructs a binary string from a set of comparisons between pixel pairs in an image patch, disregarding the neighboring pixels. This makes it sensitive to noise. This sensitivity can be reduced by prior smoothing of the image such as using the Gaussian filter. It can be 128, 256, or 512 dimensional bitstring.

ORB [9] descriptor is considered a rotation-invariant BRIEF. It steers BRIEF according to the orientation of keypoints. For a feature set of n binary tests, define a 2× n matrix which contains the coordinates of these features. Then using the patch orientation and its rotation matrix, a steered (rotated) version of the matrix can be constructed. ORB learns the optimal set of sampling pairs, whereas BRIEF uses randomly chosen sampling pairs. It uses machine learning techniques. This maximizes the descriptor's variance and minimizes the correlation under various orientation changes. An ORB descriptor has only 32 bytes.

BRISK [12] descriptor differs from BRIEF and ORB as it uses a hand-crafted sampling pattern, that is composed out of concentric rings. The pixel intensity values around each sampling point are smoothed using the Gaussian kernel. It consists of 512 binary bits.

Separate pairs of pixels are divided into two subsets, long-distance pairs and short-distance pairs. Longdistance pairs are used to determine feature orientation by computing the local gradient between them and summing these gradients. Short-distance pairs are used for the intensity comparisons that build the descriptor, as with all binary descriptors. The short pairs are rotated by the orientation computed earlier and comparisons are made between them.

• C.    Related Work

In [13], Mikolajczyk et al. presented a comparison between affine covariant region detectors and concluded that combining several detectors would lead to the best performance. They also found that all the detectors have similar performance with all types of images and transformations. However, in their comparison between SIFT, PCA-SIFT (Principal Component Analysis) and SURF detectors, Juan and Gwun [15] found that SIFT was the most stable one in all the experiments except for time whereas SURF was the fastest with good results.

A comparison of local descriptors was introduced in [14]. It showed that the performance of the descriptor doesn’t depend on the detector. Moreover, the SIFT descriptor was the best one for different image transformations except light changes. A comprehensive comparison between the recently proposed and state-of-the-art detectors and descriptors was introduced in [16]. It was in terms of number of features extracted, run time, speedup and repeatability for detectors and precision and recall for descriptors. Its conclusion was that binary descriptors are the best choice for time-constrained applications with good matching accuracy. In their work, Lankinen et al. [19] compared between a number of detectors and descriptors on different image classes. They used pairs of images of the same class for comparison, although they didn’t address any deformation issues. They used average number of corresponding regions for comparing the detectors and number of matches for descriptors.

A comparison between two patch descriptors (SIFT, SURF) and two binary ones (ORB, FREAK) has been introduced in [20]. This comparison was for Arabic character recognition on mobile devices. Its conclusion was that binary descriptors, especially ORB, yield similar results in terms of characters matching performance to the famous SIFT. However, they are faster in computation and more suitable for mobile applications. Figat et al. [21] have evaluated the performance of image features with binary descriptors. They have investigated the performance with different deformations and with different detector/descriptor combinations. Their results show that the combination of ORB detector with FREAK descriptor outperforms other combinations.

• III.    Evaluation Framework

• A.    Performance criteria

The evaluation procedure of [14] is applied in this work. It’s based on the number of correct and false matches between features extracted within an image pair. We use the number of features extracted, repeatability score as well as time for the detection stage and precision and recall for description stage.

Repeatability of a detector is the percentage of features detected again in a transformed query image.

Repeatability = # correspondences / min (n 1 , n 2 )   (1)

Where correspondences are the overlapped features between two images by a percentage of 50% using a predefined homography H and n 1 and n 2 are the number of features detected in the query and train image respectively.

Precision is the number of correct matches relative to the number of all matches between features of two images.

Precision = # correct matches / # matches        (2)

To obtain the number of matches, each feature descriptor in the query image is matched with all other features descriptors in the train image in a Brute-force manner. There is a match between two features with minimum Hamming distance. Symmetry test is then applied to the found matches to obtain only good matches. This keeps only matches between pairs ( i , j ) such that for i -th query descriptor the j -th descriptor in the matcher’s collection is the nearest and vice-versa otherwise, the match would be rejected. A match between two features ( a , b ) is correct if the error of the area covered by them is less than 30% of the region union and the difference between the first feature and the transformation of the second one by a homograhpy H is less than 3 pixels [14].

|| a- Hb || < 3                      (3)

For more consistency, the RANSAC (Random Sample Consensus) [22] algorithm is used to keep the inliers and reject all outliers. It iteratively fits a mathematical model to a selected random subset of hypothetical inliers. Finally it produces either a model which is rejected because too few points are part of the consensus data set, or a refined model together with a corresponding consensus set size. It has been widely used for this purpose. For example, Almeida et al. [23] used SIFT algorithm and RANSAC for creating a super-resolution image from a sequence of images with application of character recognition.

Recall is the number of correct matches relative to the number of correspondences.

Recall = # correct matches / # correspondences (4)

• B.    Data Set

Our evaluation is carried out on images of seven object classes chosen from the ImageNet database [24]. It is a large-scale data set of images built upon the backbone of the WordNet structure. All the test images are 375×500 pixels or vice-versa and are firstly converted into gray scale. The image sequences which represent the object classes used are leopard, books, buildings, cups, faces, trees and watches. Samples of them are shown in Fig. 1. The average entropy of images of each sequence is shown in Table 1. Each image sequence consists of 60 images, ten reference images and five artificial deformations of each image. The deformations are 2D rotation of 45°, uniform scale with a factor of 1.5, uniform reduction in the brightness with a value of 100, adding a Gaussian noise with standard deviation (σ) equal to 10 and adding a Gaussian blur with standard deviation equal to 1. In our experiments, for each sequence, features are extracted for all images and described. Then, a matching process is carried out between feature vectors in the reference image and every deformed one. The overall results for every sequence are reported.

Fig.1. Test images samples.

Table 1. Average entropy values.

Object Class	Entropy
Leopard	7.6
Books	7.0
Buildings	7.2
Cups	6.9
Faces	7.3
Trees	7.6
Watches	6.1

• C.    Implementation Details

  OpenCV [25] implementations for all detectors and descriptors are used. All the experiments have been carried out on a 2.13GHz/3MB cache Intel® Core™ i3 330M, 2GB RAM, x64 Windows 7, the code is compiled by the Microsoft Visual C++ 2010 Express with OpenCV-2.4.5.

• IV.    Experimental Resutls

In this section, the results of the performance evaluation of recent detectors and descriptors for images of different object classes are discussed. First, features are extracted in all the images by the detectors and the average number of features and the average extraction.

Repeatability is calculated as (1) for every image pair (the reference image and the deformed one) and the average repeatability is reported for every sequence. Next, those features are described with different descriptors. A Brute-Force matcher is used to match the feature vectors for every image pair and all the matches are checked to calculate the number of correct matches.

Equations (2) and (4) are used to calculate precision and recall respectively for every image pair. Then the average precision and recall are reported for every sequence. All the features are obtained with default parameters of their implementation.

• A.    Comparison of detectors

The average number of extracted features for every sequence is shown in Fig. 2. BRISK is greater than ORB only for leopard and trees. For all sequences, FAST extracts the largest number of features. In [16], the number of features extracted by SIFT was less than those extracted by SURF. However, this is true here for all sequences except for leopard and trees which have the highest variability in their visual appearance and the highest entropy values as shown in table 1.

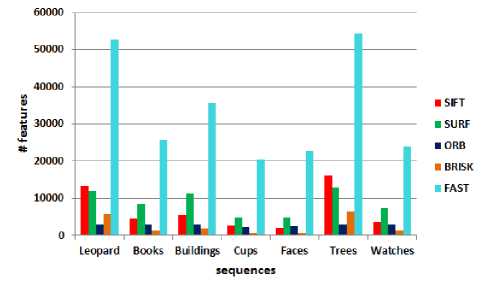
Fig.2. Average number of features.

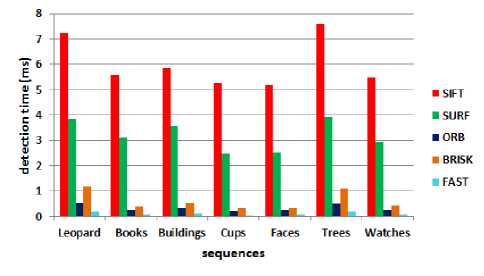
Fig.3. Average detection time in milliseconds.

For detection time, the results are the same of [16] for all sequences, although the order of extracted features numbers is different. As shown in Fig.3, SIFT is the slowest and FAST is the fastest one. There’s a big difference in detection time between SIFT and SURF and the rest.

Fig.4 presents the repeatability scores which measure the accuracy of detectors. SUFR and ORB have the best results with small difference for all sequences except for leopard and trees. Note that BRISK works better for leopard and trees. Unlike [16], FAST is the worst one.

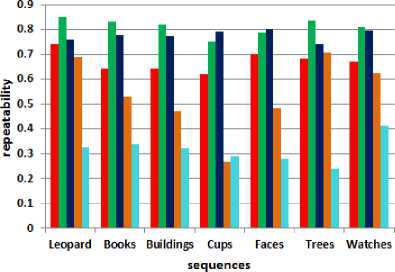
SIFT

SURF

ORB

BRISK

FAST

Fig.4. Average repeatability.

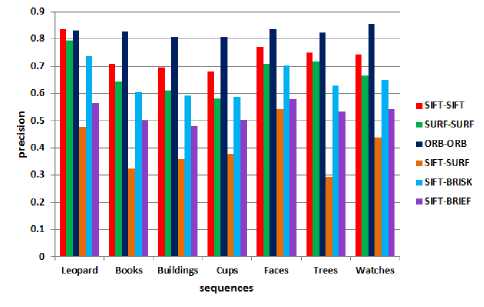
Fig.5. Average precision

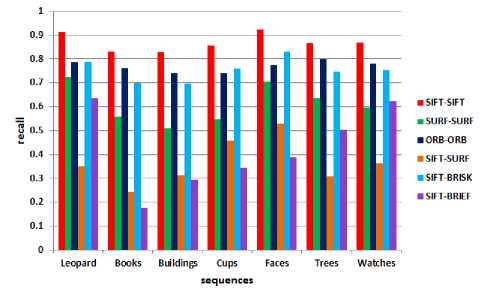
Fig.6. Average recall

• B.    Comparison of descriptors

In order to compare between descriptors, combinations are made between different detectors and descriptors. Binary descriptors are matched using a Brute-force matcher with efficient evaluation of the Hamming distance. Precision and recall are used for evaluation as shown in Fig. 5 and Fig. 6 respectively.

ORB and SIFT outperform the other descriptors for most sequences in terms of precision and recall. ORB outperforms SURF, although the difference between them decreases for leopard , trees and watches . This means that SURF works better for classes with high variability in their visual appearance.

Moreover, SURF descriptor works better with SURF features other than with SIFT features. Using SIFT detector, BRIEF is better than SURF in terms of recall for some sequences.

• V.    Conclusion

In this paper, we have presented an evaluation of local feature detectors and descriptors with different deformations on a set of images of different classes and structures. The goal was to demonstrate if and how different detectors and descriptors deal with images of different structures with the same performance level. We have used an evaluation protocol which was previously used in other evaluations. For detectors comparison FAST is the fastest detector, although it has the greatest number of extracted features for all image classes. The order of features extracted by the SIFT, SURF, ORB and BRISK differs depending on the image structure. Similarly, the order of detectors repeatability isn’t the same for different classes. For descriptors comparison, the results were more stable. ORB and SIFT obtain better results than the other descriptors for most classes, however the differences between them varies depending on the image structure. It would be interesting to evaluate feature detectors and descriptors on a wide variety of image structures in order to generalize a rule for choosing the best method suitable for a certain image structure.