Логические преобразования на кубе
Автор: Экгауз Е.Я., Цылова Е.Г.
Журнал: Вестник экономики, управления и права @vestnik-urep
Рубрика: Математика
Статья в выпуске: 4 (49), 2019 года.
Бесплатный доступ
Статья демонстрирует возможность использования свойств логических операций, законов логики и построения логических выражений не с помощью теоретико-множественной модели кругов Эйлера, а на основе трехмерной модели логического куба. Иллюстрируются возможности и преимущества такой интерпретации. Приведен список заданий, которые удобно выполнять на описанной модели.
Логические операции, логические законы, логические выражения, круги эйлера, логический куб, дизъюнктивные нормальные формы, совершенные дизъюнктивные нормальные формы
Короткий адрес: https://sciup.org/142226725
IDR: 142226725 | УДК: 51
Текст научной статьи Логические преобразования на кубе
***
Существование геометрической интерпретации для алгебраических и, в частности, логических конструкций позволяет представить их наглядно и глубже почувствовать смысл взаимосвязей их элементов. Операции над логическими элементами имеют прямой аналог в алгебре множеств. так конъюнкция соответствует пересечению множеств, дизъюнкция - их объединению, а логическое отрицание - дополнению до универсального множества. Таким образом, для интерпретации логических выражений удачно могут быть использованы круги Эйлера [1]. Однако в силу аморфности этих диаграмм (связанной с характером понятия множества) такая интерпретация теряет наглядность в случае попытки ее применения к алгебре логики, так как она не
Опыт преподавания курса «Логики» показал, что более наглядной в этом случае является интерпретация логических выражений с помощью модели «логического куба» [2].
отражает внутреннюю структуру логичес ких операций. Рис. 1. Модель «логического куба»
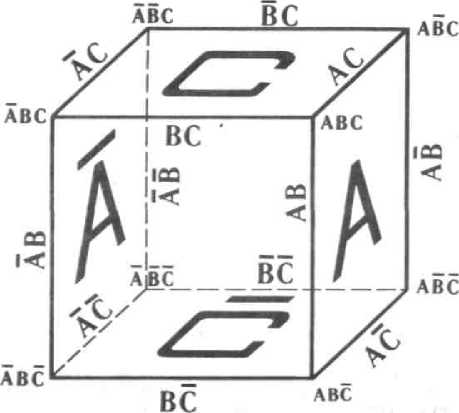
На нем удобно работать с формулами, зависящими от трех (в частности не более чем трех) переменных и приведенными к виду дизъюнктивных нормальных форм (ДНФ) [3]. В этом случае члены дизъюнкций могут быть интерпретированы как вершины, ребра и грани куба.
Интерпретация осуществляется следующим образом. Переменные и их отрицания интерпретируются как имена граней куба. Для определенности примем, что переменные A , B , C обозначают, соответственно, правую, переднюю и верхнюю грани куба, тогда граням, противоположным этим тр е м г ра н ям, естественно присвоить имена A , B , C соответственно (см. рисунок 1). Ребра куба при этом будем считать конъюнкциями прилежащих граней, а его вершины конъюнкциями граней, сходящихся в этих вершинах.
В полном соответствии с законами алгебры логики ребра куба будут являться дизъюнкциями ограничивающих его вершин, а грани - дизъюнкциями любой пары параллельных ребер, принадлежащих этой грани, или дизъюнкциями четырех вершин этой грани. В то же время вершины куба являются конъюнкциями ребер, сходящихся в этих вершинам.
Можно взглянуть на модель «логического куба» и с другой, теоретико-множественной, стороны.
Пусть куб представляет собой множество из восьми точек своих вершин, набор этих вершин будем считать универсальным множеством ( I ). Точно так же грани куба будем считать множествами из четырех точек вершин, принадлежащих этой грани, а ребра куба при этом естественно считать множествами из двух точек, принадлежащих этому ребру вершин.
Нетрудно убедиться, что логическому нулю соответствует пустое множество вершин ( ∅ ), а логической единице - универсальное множество вершин ( I ), то есть весь куб. Кроме того, операция конъюнкции соответствует операции пересечения множеств ( X ∧ Y ⇒ X ∩ Y ), операция дизъюн- кции операции объединения множеств ( X ∨ Y ⇒ X ∪ Y ), а операция логического отрицания - дополнению множества до универсального множества ( X ⇒ I / X ).
Мы видим, что грани куба представляют собой по сути объемные круги Эйлера, но при таком подходе они оказываются лишёнными аморфности, как было отмечено в начале этой статьи, а становятся конкретными, в точности соответствующими исходным высказываниям.
Для работы с моделью «логического куба» необходимо в первую очередь научиться «изображать» на модели логические формулы. Для этого необходимо преобразовать исходную формулу к виду эквивалентной ей ДНФ, то есть сначала с помощью тождества X ↔ Y ≡ ( X ∧ Y ) ∨ ( X ∧ Y ) избавиться от эквиваленций и с помощью тождества X → Y ≡ X ∨ Y избавиться от импликаций, а затем с п омощ ью законов де Морг ана [4;5] X ∨ Y ≡ X ∧ Y и X ∧ Y ≡ X ∨ Y и закона снятия двойного отрицания X ≡ X добиться того, чтобы по д знаком логического отрицания находились только отдельные переменные. Если же (или после того, как) формула приведена к виду эквивалентной ей ДНФ, она представляется в виде дизъюнкции соответствующих элементов куба (граней для одноэлементных членов ДНФ, ребер для двухэлементных членов ДНФ и отдельных вершин для трехэлементных членов ДНФ).
Модель "логического куба" позволяет наглядно убедиться в справедливости всех законов алгебры логики, в частности законов поглощения [6], наиболее тяжело понимаемых и усваиваемых.
При описанной интерпретации становятся очевидными законы поглощения: A∨(A∧B)≡ A и A∧(A∨B)≡ A . Действительно, так как A ∩B ⊆ A, B ⊆ A ∪B , то соотношения A∪( A∩ B) = A и A ∩(A ∪B) = A являются частными слу- чаями известного свойства вложенных мно- жеств: если множество X вложено в множе ство Y ( X с Y ), то X u Y = Y_, X n Y = X .
Законы поглощения A v (A л B ) = A v B и A л (A v B) = A л B также имеют нагляд- ное геометрическое толкование, так как верны соотношения Au((I/A)nB)= AuB и A n ((I / A) u B) = A n B . В первом соотношении ко второму члену дизъюнкции «добавлены» две вершины, принадлежащие ребру AB , но так как они принадлежат и грани A первому члену дизъюнкции, то в исходную дизъюнкцию новые вершины не добавляются. Во втором соотношении из второго члена конъюнкции удалены вершины, принадлежащие грани ребру AB , но так как они не принадлежат грани, первому члену конъюнкции, то исходная конъюнкция вершин не теряет.
Рассмотрим теперь более сложные законы поглощения, которые основаны на соображениях симметрии.
Пусть в трехчленной ДНФ симметрия нарушена тол ь ко по одно й из переменных (например, BC v AB v AC ). Существенная особенность такой ДНФ состоит в том, что ребра куба, являющиеся членами этой дизъюнкции, образуют трехзвенную ломаную. Если заменить звенья этой ломаной дизъюнкциями соответствующих вершин куба, то одна из вершин с р еднего звена AB буде т входить в ребро BC , а другая - в ребро AC . Таким образом, среднее звено ломаной поглощается двумя крайними звеньями, и, значит, трехзвенная ломаная эквивалентна дизъюнкции ее крайних звеньев. Итак, если в трёхчленной ДНФ симметрия нарушена только по одной из переменных, то поглощается среднее звено этой ломаной, то есть пропадает тот член дизъюнкции, который не содержит переменную, по к оторо й на р ушен а симметрия: BC v AB v AC = BC v AC .
Если же в трехчленной ДНФ симметрия нарушена дважды (например, ABv ACv BC), то этой ДНФ соответствует совокупность трех ребер куба, два из которых (в нашем случае AC и BC ) образуют двухзвенную ломаную, а третье ( AB ) скрещивается с каждым из первых двух. Если заменить звенья двухзвенной ломаной дизъюнкциями соответствующих вершин куба, то мы получим три из четырех вершин грани C , а четвертую недостающую вершину «даст» ребро. Таким образом, трехчленная ДНФ, в которой симметрия нарушена по двум переменным, эквивалентна минимальной дизъюнкции, одним из членов которой является переменная, по которой симметрия не нарушена ( C ), а другим тот член дизъюнкции, который не содержит эту переменную ( AB ). Этот член соответствует ребру куба, перпендикулярному плоскости грани C :
AB v AC v BC = C v AB .
Остаются нерассмотренными еще два случая, когда в трехчленной ДНФ, зависящей от трех переменных, симметрия нару ш ена п о всем трем переменным (например, AB v BC v AC ), и когда симметрия вообще не нарушена (например, AB v AC v BC ). В первой ситуации такой ДНФ соответствует совокупность трех взаимно скрещивающихся ребер куба, а во второй ситуации такой ДНФ соответствует совокупность трех ребер куба, исходящих из общей вершины. В обоих этих случаях рассматриваемые ДНФ являются минимальными и никакие дальнейшие их упрощения невозможны.
Для построения по имеющейся формуле соответствующей ей совершенной ДНФ (СДНФ) формула приводится к виду эквивалентной ей ДНФ, а затем представляется в виде дизъюнкции соответствующих вершин куба. При этом каждая грань куба, соответствующая одноэлементному члену ДНФ, заменяется дизъюнкцией четырех принадлежащих этой грани вершин, а каждое ребро куба, соответствующее двухэлементному члену ДНФ, заменяется дизъюнкцией двух принадлежащих этому ребру вершин.
Дизъюнкция всех восьми вершин куба является тавтологией и поэтому равна логической единице. Благодаря этому свойству по каждой формуле Ф легко можно построить ее логическое отрицание Ф . Для этого формула приводится к виду эквивалентной ей ДНФ, то есть представляется в виде дизъюнкции соответствующих элементов куба. Дизъюнкция вершин куба, не вошедших в построенную для формулы Ф дизъюнкцию элементов куба, даст формулу Ф .
Любопытно посмотреть, как на модели «логического куба» фун кцион ир у ют законы де Моргана: A v B = A л B и A л B = A v B .
Формуле A v B соответствует множество I / (A и B) вершин куба, то есть множество вершин куба, не принадлежащих ни грани A , ни грани B . Таких вершин две, и они обе принадлежат противоположному ребру AB . Отсюда следует, что A v B = A л B.
Аналогично, формуле A л B соответствует множество I / (A ^ B) вершин куба, то есть множество вершин куба, не принадлежащих ребру AB . Таких вершин шесть, и они заполняют собой противоположные этому ребру грани A и B . Таким образом, A л B = A v B.
Легко показать, что две логические формулы, зависящие не более, чем от трех переменных, эквивалентны тогда и только тогда, когда им соответствуют одинаковые множества вершин на модели «логического куба». Поэтому проверка одинаковости множеств вершин куба, соответствующих двум разным логическим формулам, является полным доказательством эквивалентности этих формул. Необходимо только помнить о том, что в модели «логического куба» предполагается, что переменные A , B , C могут обозначать произвольные (не обязательно элементарные) высказывания, но обязательно независимые и обязательно выполнимые и опровержимые (то есть не тавтологии и не тождественно ложные) выска- зывания. Если это требование не выполняется, то некоторые вершины куба могут оказаться нереализуемыми (означать противоречивые высказывания) и должны быть «выколоты» из куба.
Любопытна связь между геометрией куба (как многогранника) и комбинаторикой ДНФ, легшей в основу модели «логического куба».
Каждый трехэлементный член ДНФ устанавливает в таблице истинности ровно одну единицу и «закрывает» ровно одну строку таблицы.
Число возможных трехэлементных членов ДНФ (как и число строк в трехэлементной таб- лице истинности) равно
Г 3 )
1 3 )
" 2 3 = 8. Они
со-
ответствуют 8 вершинам куба.
Рассмотрим двухэлементные члены ДНФ. Каждый такой член устанавливает в таблице истинности ровно две единицы и «закрывает» ровно две строки таблицы.
Число возможных двухэлементных чле- нов ДНФ равно
Г 3 )
D 2 - 3 ■ 2
"2 = 2 ■4 =12 . Они соответствуют 12 ребрам куба.
Рассмотрим, наконец, одноэлементные члены ДНФ, то есть непосредственно переменные и их отрицания. Каждый такой член устанавливает в таблице истинности ровно четыре единицы и «закрывает», таким образом, ровно четыре строки таблицы.
Число возможных одноэлементных чле- нов ДНФ равно
Г 3 )
■ 21 = 3 ■ 2 = 6
(3 пере-
менных и 3 их отрицания). Они соответствуют 6 граням куба.
Мы убедились, что демонстрация логических формул на модели «логического куба» позволяет как бы «пощупать» их руками, глубже понять структуру этих формул и связь между их элементами.
Список литературы Логические преобразования на кубе
- Некрасов В.П. Основы дискретной математики: Учебное пособие. Екатеринбург: Изд- во УИЭУиП, 2011. 93 с.
- Мадер В.В. Школьнику об алгебре логики: книга для внеклассного чтения учащихся 10-11 классов средней школы: Хрестоматия. М.: Просвещение, 1993. 126 с. (Мир знаний).
- Учебник по дискретной математике ДНФ, СДНФ, КНФ, СКНФ [Электронный ресурс]. Режим доступа: http://www.mini-soft.ru/document/diskretnaya-matematika-3.
- Множества [Электронный ресурс]. Режим доступа: http://math.siomax.ru/Sets.html.
- Упрощение логических формул [Электронный ресурс]. Режим доступа: https://de.ifmo.ru/ bk_netra/page.php?dir=4&tutindex=19&index=18&layer=1.
- Беликов Д.А., Каминская Е.В. 2.1. Логические законы / Информатика. Основы алгебры высказываний: Учебно-методический комплекс. Томск, 2007 [Электронный ресурс]. Режим доступа: https://ido.tsu.ru/schools/physmat/data/res/informatika3/text/2_1.html.


