Локальная монотонная интерполяция и однопараметрические группы

В статье обсуждается использование однопараметрических групп диффеоморфизмов отрезка [ 0, 1] в тех задачах одномерной интерполяции, в которых требуется обеспечить сохранение монотонности исходных данных.

Предположим, что на отрезке [а, Ь] числовой прямой R задана сетка — набор Л из конечного числа точек ( узлов ) Х _г вида а = Х 0 <  Х 1 < ... < Х ^ = Ь ; тем самым указанный отрезок разбивается на п отрезков разбиения [Х _г , Х _{г +1} ], г = 0,..., п — 1 [1, с. 390,485]. На этом отрезке ставится задача интерполяции : для функции /: [а, Ь] щ R , значения которой У _г = /(Х _г ) в узлах сетки известны, нужно найти интерполянт — функцию F из наперед заданного семейства, определяемого конечным числом параметров, которая принимает в узлах сетки те же значения [1, с. 347 – 350].

Широчайшее применение в практике интерполяции получило использование в качестве интерпо-лянтов сплайн-функций . Это — функции, сужения которых на каждый отрезок разбиения ( звенья ) представляют собой функции одинакового строения (различающиеся лишь значениями параметров), причем во внутренних узлах сетки должны выполняться условия непрерывности низших производных сплайн-функции F , налагающие ограничения на выбор параметров звеньев [2, с. 8,20 — 21]. В частном случае полиномиальных сплайнов степени т каждое звено есть алгебраический многочлен степени т (то есть определяется т +1 параметром); если при этом F е С ^т-г [а, Ь], где число г называют дефектом сплайна, то такие сплайны образуют векторное пространство P^ _r размерности т + 1 + г(п — 1) [2, с. 20 – 21]; [3, с. 81 – 82].

Например, для кубических сплайнов дефекта 1 г-е звено сплайна зависит от 4 параметров и имеет вид

^(х) = а г + Ь г (х — Х г ) + С г (х — Х г ) ² + С (х — Х г ) ³ ;                    (1)

размерность пространства P 3\ равна п + 3. Условия интерполяции функции / дают п +1 условие на коэффициенты искомого сплайна, а задание еще двух граничных условий , налагаемых на сплайн в точках о и Ь, позволяет однозначно найти искомый интерполянт (при этом, в частности, о , = У , ). Процедура его получения хорошо известна, причем интерполяция здесь является нелокальной: значения коэффициентов сплайна зависят от всех значений У , [1, с. 392 — 393]; [2, с. 30 — 32].

2.    Задачи изогеометрической интерполяции

Предположим, однако, что об интерполируемой функции имеется априорная информация (положительность, монотонность, выпуклость и другое), и требуется, чтобы интерполянт также обладал соответствующими свойствами. Задачи такого рода называют задачами изогеометрической интерполяции [4, с. 8] или интерполяции, сохраняющей форму [5] . Кубические сплайны дефекта 1 обеспечивают сохранение формы далеко не всегда [4, с. 141].

В частности, предметом настоящей работы является строго монотонная интерполяция, при которой интерполируемая функция / либо строго возрастает на отрезке [о, Ь], либо строго убывает:

V i У + > У , либо V i У , . , < У , , (2)

и надо обеспечить строгую монотонность интерполянта F .

Задачи с монотонными исходными данными возникают во многих прикладных областях: в сопротивлении материалов (при построении диаграмм деформирования), в измерительной технике (спецификации сенсоров, цифро-аналоговых и аналого-цифровых преобразователей), в финансовой математике (модели ценообразования опционов), в фармакологии и медицинской диагностике (при построении кривых « доза — эффект » и кривых скорости оседания эритроцитов) и других [5] .

Первым к решению задач интерполяции с сохранением формы обратился Д. Швейкерт, который в 1966 году в статье [6] предложил для еe решения экспоненциальные сплайны с натяжением [3, с. 230]; [4, с. 170]. К. Де Бором был предложен альтернативный подход, в котором использовались обычные кубические сплайны дефекта 1, но к сетке добавлялись новые узлы, выбираемые специальным образом [3, с. 231 – 235]. В ряде работ применялись рациональные кубические сплайны, звенья которых — рациональные дроби с кубическим многочленом в числителе и многочленом 1-й [7] или 2-й [8] степени в знаменателе. Во всех перечисленных работах интерполянты принадлежали классу С ² и не были локальными.

В 1980 году Ф. Фрич и Р. Карлсон в статье [9] предложили локальную монотонную интерполяцию класса С ¹ кубическими сплайнами дефекта 2 и нашли те условия, при которых предложенный интер-полянт действительно будет монотонным (данный алгоритм в 1984 году был существенно упрощен [10] ). Размерность пространства P 3^₂ равна 2п+2, а звенья по-прежнему имеют вид( 1) и зависят от 4 параметров; обычно такие сплайны используют для локальной эрмитовой интерполяции (когда в узлах заданы также значения У/ = / ‘ (X , ), а значения первой производной интерполянта в узлах, называемые наклонами сплайна, должны быть такими же: Ь , = У ,’ ) [1, с. 391 — 392]; [2, с. 25 — 26]. Коэффициенты с , и / в представлении ( 1 ) вычисляются так:

h = X , +i - X , , D = " + ' -" , N = Ь , +1 - 2D + Ь , , с , = ^D - ^Ь ; — ^N , / = ^N.

h h h ²

Но Фрич и Карлсон отказались от требования интерполирования первой производной, и в их алгоритме Ь , — свободные параметры, подбором которых можно во многих случаях добиться монотонности интерполянта.

Предложенный Фричем и Карлсоном подход был развит в ряде позднейших исследований, и его современный вариант известен как интерполяция весовыми кубическими сплайнами [11]. Были найдены необходимые и достаточные условия сохранения такими сплайнами монотонности исходных данных [4, с. 141]. Изучалась также изогеометрическая локальная интерполяция рациональными кубическими сплайнами; в данном случае удается сохранить эрмитов характер интерполяции и обеспечить монотонность интерполянта уже для произвольных монотонных исходных данных, но возникает достаточно сложная проблема управления дополнительными свободными параметрами, характерными для такой интерполяции [12, 13]. Упомянем также монотонную интерполяцию рациональными тригонометрическими сплайнами (в ней каждое звено — это дробь, числитель и знаменатель которой — тригонометрические многочлены) [14].

На наш взгляд, проблемы, возникающими при монотонной интерполяции кубическими сплайнами, во многом вызваны тем, что на каждом отрезке разбиения звенья интерполянтов вида ( 1 ) образуют векторное пространство, но линейная комбинация монотонных функций из этого пространства не обязана быть монотонной функцией. Следовательно, используемая математическая структура не адекватна постановке задачи.

3.    Однопараметрические группы диффеоморфизмов

Представим, однако, г-е звено искомого монотонного интерполянта F в виде

F_t(x) = У + (У +1 - У) Г(и),                              (3)

где функция у = F^(u) — строго возрастающая функция, отображающая отрезок I = [0, 1] на себя и являющаяся при этом сохраняющим ориентацию диффеоморфизмом данного отрезка заданной степени гладкости г.

Такие диффеоморфизмы образуют бесконечномерную группу Diff + ( I ) [15] ; роль групповой операции выполняет суперпозиция функций.

В задаче эрмитовой интерполяции условия интерполирования значений самой функции / в узлах сетки и монотонности интерполянта F при этом удовлетворяются автоматически. Задача сводится к построению на каждом отрезке разбиения диффеоморфизма F t , удовлетворяющего условиям F ‘ (0) = У/Д ^ , F ‘ (1) = У ’ +i /Д _г , где Д _г = (У^ - У^ДД^ - Д^; если это будет сделано, интерполянт будет принадлежать классу С ¹ .

Начиная с этого момента, можно забыть о других отрезках разбиения и решать задачу построения локального интерполянта — такого диффеоморфизма отрезка I , первая производная которого принимает на концах этого отрезка заданные положительные значения р и q. Далее мы будем использовать букву F уже для обозначения искомого локального интерполянта, а вместо и и у писать ж и у.

В группе Diff + ( I ) можно выделить различные одномерные ( однопараметрические ) подгруппы. Каждую из них можно трактовать как образ гладкого гомоморфизма Ф: R + ^ Diff + ( I ) мультипликативной группы положительных действительных чисел в группу Diff + ( I ), сопоставляющего положительному числу к функцию F _k так, что

F _kk ‘ = F _k о F _k ‘ = F _k ‘ о F k , F i = id, F i /_k = F -                   (4)

(здесь id — тождественное отображение отрезка I на себя, то есть функция у = ж, а F — ¹ — функция, обратная к F _k : F — ¹ о F _k = id). Как будет видно из дальнейшего, нам удобнее будет работать с таким — мультипликативным — параметром (хотя в теории однопараметрических групп обычно пользуются аддитивным параметром т = ln к [16, с. 148 — 149]).

4.    Уравнение Шредера

Различные однопараметрические группы диффеоморфизмов отрезка I удобно задавать при помощи уравнения Шредера . Данное функциональное уравнение, впервые рассмотренное Э. Шредером в 1870 году в статье [17] , имеет вид

Ф(у) = к Ф(ж),                                         (5)

где Ф — вспомогательная функция ( функция Шредера ). Элементы однопараметрической группы получаются как решения уравнения ( 5 ): у = F _k (x) = Ф ^-1 (кФ(ж)) [ 18, 19] .

Заметим, что нули и полюсы функции Шредера соответствуют неподвижным точкам диффеоморфизмов Fk. Решения уравнения Шредера остаются теми же, если обе его части умножить на ненулевой множитель, возвести в степень с действительным показателем, не равным нулю, или заменить их модулями (что изменит, вообще говоря, значение к). Потребуем сейчас от функции Ф, чтобы она имела точку ж = 0 своим нулем (причем Ф‘ (0) = 1), при ж > 0 нули и полюсы чередовались, причем точка ж = 1 попадала в их число, а между соседними нулем и полюсом функция Ф изменялась монотонно. Эти требования налагают на уравнение Шредера условие нормировки и позволяют интерпретировать параметр к как значение производной функции Fk при ж = 0.

Считая в соотношении у = F _k (ж) правую часть функцией двух переменных (ж и к), рассмотрим ее мультипликативную производную по к (данное понятие известно из теории матриц [20, с. 408], а в нашем случае это — частная производная от у по к, за аргумент которой вместо ж принята переменная у):

Ру = ду ° - 1 йк Эк ° ^к

Для ее вычисления разрешим уравнение Шредера ( 5 ) относительно к:

^к = ^Ф(у^)/Ф(ж) = ^{| Ф(}у) | / ^{| Ф(ж) |}

(вставка знаков модуля законна, так как у Ф(ж) и Ф(у) знаки одинаковы), после чего возьмем логарифм от обеих частей равенства и продифференцируем полученное соотношение по к:

1 = (in |ф(у)1)’ |у, к              дк откуда

Ру ₌ м (у) йк      к ,                                        ⁽⁾

где функция М (у) = 1/(in | Ф(у) | ) ‘ от к уже не зависит; ее можно трактовать как значение мультипликативной производной в единице группы R + , то есть при к = 1.

Если теперь, считая к мало отличающимся от 1, разложить Fk (ж) по степеням параметра т = in к, то коэффициент при первой степени т будет равен значению при т = 0 производной dFk(ж) = ду йк = ду к.

дт дк йт дк ’ приняв за аргумент переменную у, получаем, что данный коэффициент совпадает с М(у) (впрочем, при т = 0 у = ж).

Отметим, что произведение данного коэффициента на оператор частной производной представляет собой инфинитезимальный оператор U однопараметрической группы [16, с. 143 — 144]. Таким образом,

U = М (ж) М .                                 (8)

дж

5.    Случай дробно-линейной интерполяции

Переходим к рассмотрению частных случаев интерполяции диффеоморфизмами. Начнем с простейшего примера функции Шредера, соответствующей наложенным выше требованиям (в теории динамических систем данный пример хорошо известен [19] ):

ф(ж) = мм   Ф-М) =

«ж|

(здесь и далее ж = Ф(у) = /3 Ф(ж), параметр группы в данном частном примере мы обозначаем /3, а не к). Решение уравнения Шредера Ф(у) = /3 Ф(ж) имеет вид у = F =           .

1+рж - ж

Дробно-линейные функции вида ( 10 ) находят применение не только в задачах интерполяции (например, в [21, с. 33 – 34] при помощи таких функций задавался закон движения рабочей точки робота-манипулятора). При /3 = 1 график такой функции на отрезке I — дуга равнобочной гиперболы с асимптотами, параллельными координатным осям (Рис. 1,2).

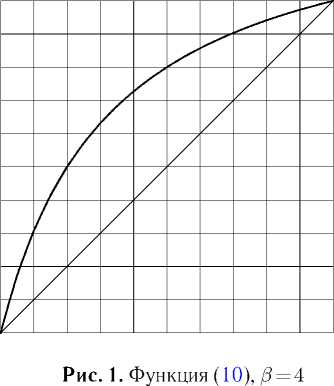
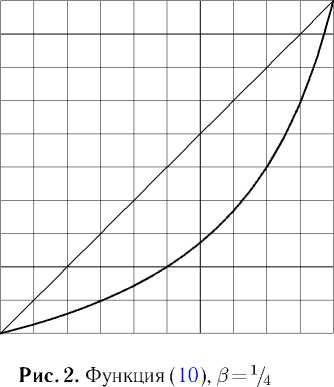
Вычисление инфинитезимального оператора однопараметрической группы диффеоморфизмов вида ( 10 ) (которую обозначим G ^a ) дает:

U = М (ж) — = ж(1 -ж) — . дж          дж

Отсюда видно, что диффеоморфизмы из группы G a не имеют на отрезке I неподвижных точек, кроме 0 и 1. Первая производная функции Fg по ж имеет вид п =

3        .

(1+3ж - ж) ² .

на отрезке I она при 3 = 1 изменяется монотонно, принимая на его концах значения 3 и 1/3.

Таким образом, функции вида ( 10 ) могут служить для эрмитовой интерполяции на отрезке I при условиях р = 3 и q = 1/3.

Отметим одно важное свойство локальных интерполянтов, являющихся элементами однопараметрической группы диффеоморфизмов. Если выполнить обратную интерполяцию (построить интерпо-лянт для функции, обратной к задаваемой [1, с. 422]), а затем обратить полученный интерполянт, то — в силу последней из формул ( 4 ) — результат совпадет с интерполянтом, полученным непосредственно. Данное свойство будем называть инверсной инвариантностью процедуры интерполяции.

Логичность использования функций вида ( 10 ) в качестве локальных эрмитовых интерполянтов подкрепляется следующими соображениями. Известно, что на множестве заданных на отрезке [Х _г , Х _г +1 ] функций у = у (ж) класса С 4 , удовлетворяющих на концах отрезка условиям

у(Хг) = Y,     у(Хг+1) = Y+1,     у'(Хг) = Y',     д'(Хг+1) = Y+i, тот кубический многочлен вида (1), для которого эти условия выполнены, доставляет минимум функционалу

• ^{1    (}у) = /     ь^(ж,у^,у ' ^,у"Н^ж,

  
  

J Xi в котором L(ж,у,у,,у") = (у'')2 [22, с. 25—26]. Необходимым условием экстремума функционала (13) является уравнение Эйлера d2 dL   d dL  dL _ dж2 ду" dж ду'   ду ’ принимающее в данном случае (после сокращения на множитель 2) вид у "' ' = 0;

многочлены вида ( 1 ) дают общее решение данного дифференциального уравнения.

Экспоненциальные сплайны с натяжением Швейкерта доставляют минимум функционалу с функцией Лагранжа L(x, у, у’, у'') = (у'' —Ау')2, а уравнение Эйлера принимает вид у'''' — А 2у" = 0 , где А > 0 — параметр натяжения [22, с. 19—20].

Учитывая, что при монотонной интерполяции на отрезке I первая производная интерполянта должна быть заведомо положительна, можно попробовать вместо минимизации квадрата второй производной минимизировать квадрат производной от логарифма первой производной искомого интерполянта у = g(x) при условиях

9⁽⁰⁾=⁰ ,     9⁽¹⁾ = ¹,      д' ⁽⁰⁾ = Р,     д ' ⁽¹⁾ = q.

При этом имеем:

L(x,у,у',у") = (у")²/(у')² .                                     (14)

Уравнение Эйлера принимает вид у''"      4 у "у'''     3 (у' ')3

(у ' ) ²        (у ' ) ^{3 +}   (у ' ) ⁴

Поскольку переменная у явно в (15) не входит, переходом к переменной s = у’ понижаем порядок уравнения; избавляясь от знаменателей, имеем:

s ² s ''' — 4 ss's " + 3(s '' ) ³ = 0 .

Переменная x в данное уравнение также явно не входит; поэтому можно еще понизить порядок, полагая и = s'/s (на минимизацию и2 как раз и направлены наши усилия). Получаем дифференциальное уравнение и" — и и' = 0 .

Последнее допускает первый интеграл

и

— Т = ^2Д.

Следовательно, переменная и удовлетворяет дифференциальному уравнению первого порядка ( 16) ; это — частный случай специального уравнения Риккати. Общее решение данного уравнения известно [23, с. 296]; вводя обозначение и(0) = 2S, его можно записать в виде:

при R = 0 и при R< 0 и при R> 0 и

2S

1 — S x ’

2Sk — 2k2 th kx к — S th kx k == —RR;

k = Vr.

2Sk + 2k ² tg kx к — S tg kx

В случае R = 0 с учетом того, что переменная s всюду положительна на I , получаем для s выражение

_ В 8 = (1 —Sx)2 ’ где В — новая постоянная интегрирования. Сопоставляя это с (12), находим, что В = 3 и S =1— 3.

Таким образом, дробно-линейные функции вида (10 ) являются частными решениями уравнения Эйлера ( 15 ) и доставляют минимум квадрату производной от логарифма первой производной интерполянта при условиях р = 3 и q = 1/3.

6.    Симметричный случай

Рассмотрим теперь следующий, симметричный случай, когда р = q = 7. Здесь выбор однопараметрической группы G ^s не является столь очевидным. Попытка искать локальные интерполянты среди решений уравнения ( 15 ) при R = 0 не приводит к успеху. Эти решения, правда, можно найти в явном виде; каждое из них представимо как дробь, в числителе которой фигурирует sh кх (при R< 0) или sin кх (при R> 0), а в знаменателе — линейная комбинация ch кх и sh кх (соответственно, cos кх и sin кх).

Но попытка выразить коэффициенты этих дробей через данные из условий интерполяции приводит к необходимости решать трансцендентные уравнения. Кроме того, такие интерполянты не образуют однопараметрических групп и не обладают инверсной инвариантностью. Это означает, что выбор минимизируемого функционала (13) с функцией Лагранжа (14) в задачах монотонной интерполяции не является наилучшим.

Заметим, однако, что при рассматриваемом сейчас условии на параметры р и q при 7 = 1 график ин-терполянта обязательно должен пересекать главную диагональ единичного квадрата I х I , и естественно потребовать, чтобы искомые диффеоморфизмы имели неподвижную точку при х = 1 / 2 . Забегая вперед, отметим: во всех рассмотренных ниже случаях график производной Е ^ (х) окажется при 7 = 1 симметричным относительно вертикальной оси симметрии упомянутого квадрата, имея экстремум при х = 1 / 2 (график же самой функции F ₇ (х) будет иметь при этом значении х точку перегиба).

Во-первых, рассмотрим такую функцию Шредера:

Ф(х) =

х (1 - х) 1 - 2х

Вычисляя инфинитезимальный оператор соответствующей однопараметрической группы G ₁ ^s , получаем:

, . д

U i = М (х) — = дх

х (1 - 2х)(1 - х) д х ² + (1 - х) ² дх ’

а явный вид диффеоморфизмов из G ₁ ^s таков:

х - 1 / 2

^{У 7     2    2} ^ (7х(1 - х)) ² + (х - 1 / 2 ) 2 + 7х(1 - х)

■

Диффеоморфизмы отрезка [ - 1, 1], получаемые из функций ( 19 ) линейной заменой переменных, использовались при решении некоторых задач управления движением механических систем: здесь управляющий момент периодически зависел от обобщенной координаты, и данные диффеоморфизмы обеспечивали нужную модификацию такой зависимости [24, 25] .

При 7 = 1 график функции вида ( 19) на отрезке I (Рис. 3) — дуга алгебраической кривой 3-го порядка (в рамках восходящей к Ньютону классификации кривых 3-го порядка — адиаметральной гиперболической гиперболы [26, с. 7 - 9]). При х = 1 / 2 имеем: F 7 (х) = 1/7.

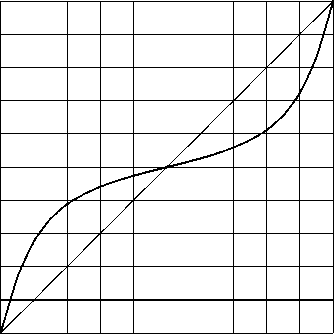
Рис. 3. Функция ( 19 ), 3 = 4

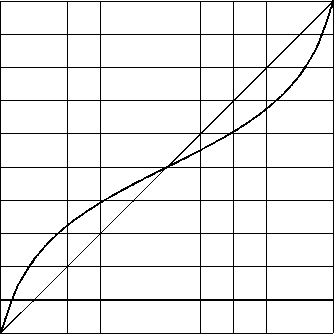
Рис. 4. Функция ( 22 ), 3 = 4

Во-вторых, рассмотрим инфинитезимальный оператор более простого вида:

U2 = M (ж)    = ж (1 — 2ж)(1 — ж) -I-                           (20)

дж                дж и найдем соответствующую функцию Шредера.

Для этого представим соотношение ( 7 ) в виде дифференциального уравнения с разделяющимися переменными:

d7         dy

7     У (1 —2У)(1 —У) ’ после чего разложим рациональную дробь 1/M(y) на элементарные дроби:

d7 = ( 1      4 \

7    \У    1 —2У    1 —У/ У и проинтегрируем данное уравнение по 7 в пределах от 1 (когда у = ж) до текущего значения 7:

ln7 = ln |у| — 2ln |1-2у| + ln |1 — у| — ln |ж| + 2ln |1 —2ж| — ln |1 — ж|, откуда

У ^{(1 — 2ж)} 2 ^{(1 —} У) ж (1 — 2у) ² (1 — ж)

Таким образом, ж (1 — ж)

*<*> = (1 — ж) 2 •

Разрешая уравнение Шредера Ф(у) = 7 Ф(ж) относительно у , получаем явный виддиффеоморфиз-мов из новой группы G ₂ ^s :

^У = ⁷ =2 + 2    ■

ж — 1 / 2 _________ — ж) + (ж — 1 / 2 ) 2 •

При 7=1 график такой функции на отрезке I (Рис. 4) — дуга алгебраической кривой 4-го порядка. Внешне он весьма схож с графиком функции ( 19 ), однако при ж = 1 / 2 теперь имеем: Р^ж) = 1/ ^ 7.

Наконец, выполним для функции ( 19 ) процедуру эрмитовой интерполяции сплайном со звеньями вида ( 3 ), приняв за узлы точки 0, 1 / 2 ,1. Полученный интерполянт оказывается диффеоморфизмом отрезка I класса С 1 , а график его при 7 = 1 есть кривая, составленная из двух дуг равнобочной гиперболы, стыкующихся при ж = 1 / 2 .

Нетрудно показать, что и такие диффеоморфизмы, образующие группу G ₃ ^s , вполне соответствуют рассматриваемой схеме. Здесь функция Шредера имеет вид

Ф(ж)

min (ж, 1 — ж) (1 — 2ж)    ’

инфинитезимальный оператор группы — вид

д min (ж, 1 — ж) • (1 —2ж) —— , дж

U3 = M (ж) — дж а явный вид диффеоморфизмов из G3s таков:

У = FL = - + -

^{У 7}     2 ⁺ 2

__________ ж — 1 / 2

7 ^{( 1 /} 2 ^{— | ж — 1 /} 2 ^{| ) + | ж}

¹ / 2 | ^•

Далее мы предполагаем, что в качестве группы G ^s выбрана одна из групп G ₁ ^s , G ₂ ^s , G ₃ ^s .

7.    Общий случай

Переходим к рассмотрению общего случая интерполяции диффеоморфизмами, когда р и q — произвольные положительные числа. Можно было бы искать локальный интерполянт как элемент новой однопараметрической группы диффеоморфизмов отрезка I , инфинитезимальный оператор которой есть линейная комбинация одного из операторов ( 18 ), ( 20 ) или ( 24 ) и оператора ( 11 ) с коэффициентами 9 и 1 - 9, подбирая надлежащим образом значения группового параметра и параметра 9.

Однако выражения для получаемых на этом пути функций Шредера будут произведениями двучленов, возведенных в степени с произвольными (в общем случае) действительными показателями, и нахождение явной формулы для искомого интерполянта становится затруднительным.

Мы пойдем по другому пути: будем строить искомые интерполянты как суперпозиции диффеоморфизмов из уже рассмотренных групп G ^a и G ^s .

Для сохранения инверсной инвариантности будем строить интерполянт не в виде F ₇ oF g или F g oF ₇ , а в таком виде:

_

F = Fg o F7 o Fg , где Fg — функциональный квадратный корень из функции Fg (то есть такая функция, что Fg =

̂︀

̂︀̂︀

F g oF g [18] ). В нашем случае в силу ( 4 ) F g = F g g .

По теореме о дифференцировании сложной функции имеем:

р = V3 '7 • V3    и q = (1/V^) -7 • (1/V3) , откуда

3 = VP/k,    7 = V pq.                            (27)

Таким образом, интерполянт вида ( 26 ) является искомым диффеоморфизмом отрезка I , первая производная которого принимает на концах отрезка заданные значения р и q. Возвращаясь к задаче интерполяции функции / на всем отрезке [а, Ь\, в соответствии с ( 3 ) получаем, что г-е звено искомого монотонного интерполянта имеет вид

F , (х) = Y , + (Y _{i +}i -Y)F g (F ₇ (F g (u))),     где u = (х-Х _г )/(Х _г +1 -Х_г) .       (28)

Если 7 = 1, а значение 3 мало отличается от 1, то график интерполянта ( 26 ) по-прежнему будет иметь точку перегиба, но она уйдет с главной диагонали единичного квадрата I х I . Если же 3 ^ 1 или 3 ^ 1, то точки перегиба на отрезке I уже не будет.

Заметим также, что функция F ₇ (мы вновь предполагаем, что 7 = 1) под действием внутреннего автоморфизма отрезка I , порожденного каким-либо элементом группы G ^a , переходит в новую функцию

F 7 = F g o F 7 oF - ,                              (29)

для которой по-прежнему выполняются условия р = q = 7, но точка перегиба смещается вдоль главной диагонали единичного квадрата I x I влево (при 3> 1) или вправо (при 3< 1); параметр 3 здесь не связан с параметром 3, определенным в соответствии с ( 27 ).

Заменяя в ( 26 ) F ₇ на F ₇ (первый и последний функциональные множители в ( 29) при этом можно объединить с соответствующими множителями в ( 26 )), мы получаем модификацию изложенной выше процедуры локальной эрмитовой интерполяции. В такой модификации фактически присутствует свободный параметр (которым можно распоряжаться, стремясь точнее воспроизвести особенности интерполируемой функции). При этом вместо формулы ( 26 ) интерполянт задается формулой

F = F g i o F 7 o F g 2 ,                                   (30)

где параметры 3 1 и 3 2 выбирают так, чтобы 3 1 3 1 = V p/q.

Однако далее мы обсуждать эту модификацию не будем.

Упомянем также, что при эрмитовой интерполяции предложенным способом функции класса С ⁴ при стремлении максимального шага h сетки Л к нулю погрешность интерполяции (то есть норма || / — F || , равная максимуму модуля разности / — F на отрезке [а, Ь] [2, с. 10]) ведет себя как O(h ⁴ ) (в самом деле, именно такую погрешность имеет эрмитова интерполяция кубическими сплайнами дефекта 2 [1, с. 392]; [3, с. 49]; а для / и ее интерполянта вида ( 28 ) интерполирующий кубический сплайн из Р ^₂ — один и тот же). К случаю G ^s = G 3 эти рассуждения, впрочем, не применимы.

Если же значения ¥^ первой производной в узлах Х _г не заданы, то их можно найти приближенно. При локальной интерполяции кубическими сплайнами стандартный способ — построить для каждого г вспомогательный многочлен 2-й степени, интерполирующий / в узлах Х _{г -1} , Х _г , Х _г +1 (его графиком служит парабола); значение ¥ ‘ его производной в узле Х _г используют вместо ¥ _г ‘ . После этого применяют обычную технику эрмитовой интерполяции; получаемый кусочный многочлен называют кубическим многочленом Бесселя , а погрешность такой интерполяции — O(h ³ ) [ 1, с. 422 — 423]; [3, с. 50].

Однако такая процедура не гарантирует положительности ¥ _г ‘ при возрастающих значениях ¥ _г . Вместо нее при монотонной интерполяции поэтому часто используют метод геометрического среднего [13] . В обсуждаемом же здесь случае интерполяции функциями вида ( 28 ) естественно применить другой прием: интерполировать для каждого г значения / в узлах Х _{г- 1} , Х _г , Х _{г +1} дугой равнобочной гиперболы.

Именно, преобразуем линейной заменой переменных прямоугольник [Х _{г- 1} , Х _г +1 ] х [¥ - 1 > ¥+1 ] в единичный квадрат I х I ; точка с координатами (Х _г , ¥ _г ) перейдет при этом во внутреннюю точку данного квадрата с координатами (5, у). Разрешая уравнение Шредера Ф(у) = 3 Ф(т) с функцией Шредера вида ( 9 ) относительно 3, находим для интерполянта вида ( 10) следующее значение параметра:

3 = IS • (31)

Теперь по формуле ( 12 ) вычисляем значение производной и возвращаемся к исходным переменным. Рассмотрим некоторые примеры эрмитовой интерполяции функциями вида ( 28 ).

8.    Примеры

Пример 1. Рассмотрим на отрезке [0, 1] функцию у = е ^Кх , К >  0 (в последующих расчетах принято К = 4).

На рисунках (Рис. 5 – 6) представлены результаты интерполирования данной функции соответственно эрмитовыми кубическими сплайнами и функциями вида ( 28 ) в простейшем случае, когда число п отрезков разбиения равно 1 (функциональный сомножитель в ( 26 ) был выбран из группы G S ).

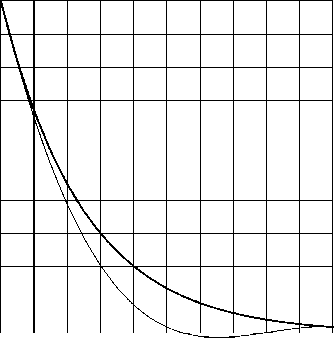
Рис. 5. у = е ^Кж : интерполянт из P ^₂ , п =1 Рис. 6. у = е ^Кж : интерполянт вида ( 28) , п =1

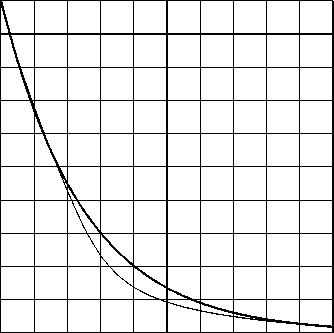
Видно, что эрмитов кубический сплайн (который в данном случае сводится к кубическому многочлену) не сохраняет монотонность исходной функции (и даже принимает на некотором промежутке отрицательные значения), а предлагаемый здесь интерполянт монотонность сохраняет и в целом воспроизводит поведение интерполируемой функции.

Разумеется, шаг, равный 1, здесь слишком велик. Будем последовательно сгущать используемые сетки, каждый раз деля отрезки разбиения пополам. Уже при п = 2 проблемы с монотонностью у эрмитова кубического сплайна исчезают (хотя они возникают вновь, если увеличить значение К ). Нормы погрешности с увеличением п ведут себя следующим образом:

п	1	2	4	8	16	32
А	0.119	0.0165	0.00161	0.000127	0.00000899	0.000000597
В	0.072	0.0133	0.00204	0.000283	0.00003741	0.000004786
С	0.059	0.0082	0.00080	0.000064	0.00000449	0.000000298
D	0.067	0.0113	0.00155	0.000197	0.00002448	0.000003025

(строка А отвечает интерполянтам из P ^₂ , а строки В, С и D — интерполянтам вида ( 28) при выборе в качестве реализации группы G ^s групп G -s , G 2 и G 3 соответственно). Видно, что при малых п интерполянты вида ( 28 ) обеспечивают по сравнению с эрмитовыми кубическими сплайнами лучшее приближение, а с ростом п все четыре интерполянта имеют примерно одинаковую точность.

Пример 2. Рассмотрим набор данных, предложенный в 1970 году Х. Акимой и часто используемый при тестировании алгоритмов монотонной интерполяции. Поскольку в настоящей работе обсуждается строго монотонная интерполяция, данные Акимы (взятые из [13] ) были модифицированы: к значениям Y были добавлены значения функции 0.1 ж в узлах сетки, а значения Y ’ — увеличены на 0.1. В результате был получен следующий набор данных:

Х г	0	2	3	5	6	8	9	11	12	14	15
Y	10.0	10.2	10.3	10.5	10.6	10.8	11.4	16.1	51.2	61.4	86.5
У	0.1	0.1	0.1	0.1	0.1	0.1	1.450	14.121	18.397	14.720	36.696

На рисунке (Рис. 7) представлен результат интерполирования этих данных сплайном F со звеньями вида ( 28 ) (для определенности была выбрана группа G ₁ ^s ). Интерполянт сохраняет монотонность данных (в то время как при интерполяции данных Акимы эрмитовыми кубическими сплайнами, сплайнами с натяжением Де Бора и методом Акимы интерполянт теряет монотонность на предпоследнем отрезке разбиения [9, 13] ).

Заметим также, что функция у = F (ж) — 0.1т служит монотонным интерполянтом для исходных данных Акимы.

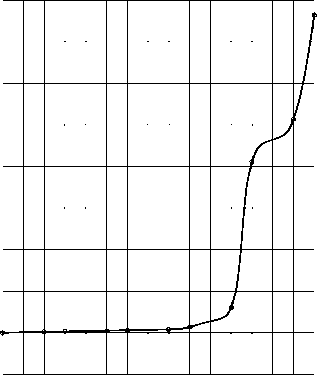
Рис. 7. Интерполянт вида ( 28 ) для модифицированных данных Акимы

9.    Заключение

В данной работе предложена процедура локальной эрмитовой сплайн-интерполяции класса С ¹ для строго монотонных данных, в рамках которой локальные интерполянты представляются в виде суперпозиций диффеоморфизмов единичного отрезка [0, 1], принадлежащих некоторым однопараметрическим группам таких диффеоморфизмов. Данная процедура приводит к достаточно простым расчетным формулам, а свойство строгой монотонности для получаемого интерполянта гарантировано. Обсуждаются свойства таких интерполянтов, приведены результаты вычислительных экспериментов.