Локальная разрешимость и разрушение решения одного уравнения с квадратичной некоэрцитивной нелинейностью
Автор: Корпусов Максим Олегович, Лукьяненко Дмитрий Витальевич, Овсянников Евгений Алексеевич, Панин Александр Анатольевич
Рубрика: Программирование
Статья в выпуске: 2 т.10, 2017 года.
Бесплатный доступ
Рассмотрена начально-краевая задача для уравнения ионно-звуковых волн в плазме. При этом распределение Больцмана плотности электронов приближено квадратичной функцией. Для рассмотренной задачи доказана локальная (по времени) разрешимость и проведено аналитико-численное исследование разрушения решения. Методом пробных функций получены достаточные условия разрушения решения за конечное время и оценка сверху на время разрушения. В конкретных численных примерах эти оценки уточнены численно методом сгущения сеток по Ричардсону. Промежуток времени для численного счета выбирается согласно аналитически полученной оценке сверху на время разрушения решения. В свою очередь, численное моделирование уточняет момент и характер этого разрушения. В частности, показано распространение разрушения в пространстве. Таким образом, аналитическая и численная части исследования взаимно дополняют друг друга.
Разрушение решения, нелинейная начально-краевая задача, уравнение соболевского типа, экспоненциальная нелинейность, экстраполяция по ричардсону
Короткий адрес: https://sciup.org/147159418
IDR: 147159418 | УДК: 517.957+519.6 | DOI: 10.14529/mmp170209
Текст научной статьи Локальная разрешимость и разрушение решения одного уравнения с квадратичной некоэрцитивной нелинейностью
В этой работе мы продолжаем исследования нелинейных уравнений, описывающих уравнения ионно-звуковых волн в различных модельных предположениях и начатые в работах [1-4]. В данной работе мы рассмотрим следующую модельную ≪ 1 + 1 ^ -мерную задачу:
∂ 2
dt2 u xx — £u
^^^^^^
ε 2 2
— u + U xx =0 при
( x,t ) G (0 ,l ) х (0 ,T ) ,
Ux (0,t) = Ux (l,t) = 0 щill t G [0,T],(2)
u(x, 0) = u0(x), ut(x, 0) = u 1(x) щ>n x G [0,l].(3)
Решение мы будем искать в классе u(x,t) G C(2)([0,T]; C(2)[0,l]). Поэтому нам с необходимостью нужно потребовать выполнимость условий согласования начального и граничного условий u0x (0) = u0x (l) = u 1 x (0) = u 1 x (l) = 0.( 4 )
Уравнение (1) описывает нелинейные ионно-звуковые волны в плазме с очень большим радиусом Дебая rD =
kTe А1 /2
-
4 ne2 n 0, r
Ниже приведен вывод уравнения (1) в многомерном случае. Затем мы докажем локальную во времени классическую разрешимость и получим достаточное условие разрушения решения задачи (1) - (3) за конечное время и получим оценку сверху на это время.
1. Вывод уравнения
Рассмотрим ионно-электронную плазму в области D С R N , N > 1. В приближении квазистационарного электрического поля имеют место следующие уравнения:
div E = - 4 nen, rot E = 0 ,
где E - это вектор напряженности электрического поля, n = n e + n i - это суммарная плотность электронов и ионов. В предположении, что область D является поверхностно односвязной, можно ввести потенциал электрического поля ф, связанный с вектором E равенством
E = -Уф. (6)
В этом случае плотность электронов хорошо описывается распределением Больцмана ne = n0 exp
k e T ϕ e ,
где n0 - равновесная плотность электронов, Te - температура электронов. А для концентрации ионов n i справедливо уравнение неразрывности
V = div J ■ ∂t где J - это плотность тока ионной составляющей плазмы и учитывает временную дисперсию
t
J = ^а ( t,T )E( т ) dr, а ( t,T ) G C(2)([0 ,T ] ® [0 ,T ]) .
Из уравнений (5) - (7) мы получим следующее дифференциальное следствие:
kT^ = 4 ne n i - (Ю)
Из системы уравнений (8) и (9) мы получим следующее дифференциальное следствие: t
а ( t,r )А ф ( т ) dr. (11)
А ф — 4 nen0 exp (
∂n i
∂t
-
/
Из уравнений (10) и (П) вытекает дифференциальное следствие
t dt ^А ф - 4 nen 0 exp (el^ ) + 4 ne J a (t, т )А ф (т) dr = 0.
e 0
В одном частном, но важном случае а ( фт ) = а0 > 0 мы приходим к следующему дифференциальному следствию:
^ 2 1а ф — 4 nen 0 exp (фф ) + 4 nea оА ф = 0 .
Сделаем в этом уравнении замену и = 4 п^П 0 , тогда получим следующее уравнение:
^ (А u - exp (д))
+ 4 nea 0А и = 0 ,
где
/ kT e V / 2 r D = ^4 пе^
это так называемый радиус экранировки Дебая. В случае плазмы радиус Дебая
достаточно большой настолько, что можно ограничиться рассмотрением первых трех членов разложения функции exp( eu ) по малому параметру E = 1 /г^:
exp( eu ) = 1 + eu + — и 2 + o ( e 2 и 2) .
Из уравнений (14) и (15) вытекает искомое уравнение:
∂ 2
дё (А U - EU
^^^^^^
ε 2
—и 2 J + А и = 0 ,
в котором мы коэффициент 4 пеа 0 при елагаемом Ли заменили единицей.
2. Локальная разрешимость
Будем доказывать локальную во времени разрешимость задачи (1)
- (3) в
классе C(2)([0 ,T ]; C(2)[0 , l ]). Введем функцию Грина дифференциального оператора - ddx 2 + E I, Е > 0 ’
G . ( x ,y ) ^Ё sinh( ^El ) I
cosh( y/Ex ) cosh( Д Е ( y — l )) , cosh( у/Ey ) cosh(Д Е ( x — l )) ,
прп x < y ; npii x > y.
Перепишем рассматриваемое уравнение для удобства в эквивалентном виде
d 2 (-Ux , + EU + E- U 2^ dt 2 2
^^^^^^
u xx + EU = EU.
В классе гладкости C(2)([0 , T ]; C(2)[0 ,l ]) с учетом введенной функции Грина получим интегродифференциальное равенство
где
∂ 2 ε 2
dtp и + у G . u + и = eG . u,
l
G . f = /G. ( x, y ) f ( y ) dy.
Проинтегрируем равенство (17) один раз по времени, тогда получим равенство
где
t
∂ ε 2
dt {и + -— G . u 2 1 = и 1( x )+ e 2 G ( и 0 и 1)( x )+ ds (^—и ( x , s )+ eG . u ( s )J ds, (18)
l
G ( и о и i)( x ) = У G . ( x,y ) и о( у ) и i( y ) dy.
Заметим, что
° (и + Ё 2 G . и 21 = ( I + K . . ) dU dt у 2 dt
где I - это единичный оператор, а
/X
K 5 ( u )
l
* w = Iе 2 G . ( x.y ) u ( y.t ) w ( y.t ) dy .
Тогда уравнение (18) можно переписать в следующем виде:
du
I + Ке ( u ) * — dt
t
= u i ( x ) + 6 G ( и о u 1)( x ) + Ids( u ( x.s )+ ,G.u ( s )) ds. (22) 0
Рассмотрим банахово пространство B = L“ ((0 ,T ) x (0 1 ) )) , где T > 0 - произвольное фиксированное. Точно так же, как и в [1], можно доказать, что
\\К . ( v ) *\ |B ~ B 6 С 1( ) )Ф 1 1 ,
где ||-\ в ^ в - это операторная норма линейного пространства всех линейных непрерывных операторов, действующих из B в B. Введем теперь замкнутое, ограниченное и выпуклое подмножество банахова пространства B :
B ^n = { v ( x,t ) е B : || v| k~ ((о t ) X (о ,T )) 6 An} ,
\u о \ I l ~ (о ,i ) 6 A. \u 1 \ I l ~ (о ,i ) 6 A.
где n = n ( T ) е N некоторое фиксированное, котopoe мы фиксируем позже, a a = A ( T,e ) > 0 - достаточно малое чпыто. Прп фиксированных T, ), е п n выберем a > 0
настолько малым, чтобы
c 1( ) ) еап 6 2 ■
В этом случае оператор (I + КС. (и) *) существует и представим в виде ряда Ней мана
( I + К . ( и ) * ) - 1 = ^ [ - К . ( и ) * ] m m =о
Следовательно, уравнение (22) можно переписать в виде du
— = ( I + K . ( u ) * dt
t и 1( x) + е 2 G( и о и 1) + У ds ——и (x, s) + e . Далее это уравнение можно проинтегрировать один раз по времени и получить следующее равенство: t и (x,t )= и о (x) + У A (и)(x,s) ds, о где A (и)(x,t ) = (l + К. (и) *) t и i( x)+ е 2 G( и о и 1) + ^ ds ——и (x,s)+ eG .и (s)) dsj ■ (28) о ПО Точно так же, как в [1,2], можно доказать, что при выборе N Э n > 4T + 1 - фиксированном и при достаточно малом ц > 0 имеют место следующие свойства A(u) : B,n ^ B,n, \\A(v 1) - A(v2)\\ 6 2\\v 1 - v2\, т.е. оператор A(v) является сжимающим на B^n. Используя вариант принципа сжимающих отображений работы [5], можно доказать существование единственного решения u(x,t) Е B^n С B интегрального уравнения (27). Далее так же, как и в [1], нужно воспользоваться «бутстэп»-методом для повышения гладкости решений интегральных уравнений и получить, что на самом деле решение интегрального уравнения (27) принадлежит классу u(x,t) Е C(2)([0,T]; C(2)([0,l])). Стало быть, нами доказана следующая теорема: Теорема 1. Пусть фиксированы исходные параметры задачи: е > 0,l> 0. Тогда для произвольного T > 0 найдете я такое ц > 0, что при достаточно малых начальных функ'1щй u0(x) Е C(2)([0,l]) 11 u 1(x) Е C(2)([0,l]) : \u0\l^(0,i) 6 Ц, \u 1 \l^(0,i) 6 Ц, удовлетворяющих условиям u0x (0) = u0x (l) = u 1 x (0) = u 1 x (l) = 0, существует единственное решение рассматриваемой задачи в классе u(x,t) Е C(2)([0,T]; C(2)([0,l])).
3. Разрушение и оценка времени разрушения решения Пусть u(x,t) Е C(2)([0,Т]; C(2)[0, l]) - это локальное единственное решение задачи (1)-(3). В этом разделе мы докажем, что T 6 Ты = У (u0(x) - е) dx при достаточном условии, что -1 - 2 У ^u0(x) ^ u 1(x) dx Потребуем выполнения условия (30). Тогда сразу же приходим к искомой оценке (29), поскольку при t > T^ равенство (32) становится противоречивым.
4. Численная диагностика разрушения решения В этом разделе мы детально обсудим методы, которые помогут нам численно диагностировать факт разрушения решения и уточнить его локализацию как во времени, так и в пространстве. Напомним, что априорная информация, полученная аналитически в разделе «Разрушение и оценка времени разрушения решения», дает нам оценку времени разрушения решения, однако не дает детального описания процесса разрушения. Численный же подход, использующий аналитически полученную априорную информацию, может помочь детализировать процесс разрушения и уточнить момент разрушения. Будем использовать обозначения uinit0 (x) ,uinit 1 (x) вместо u0(x) ,u 1(x) в связи с тем, что мы используем подобные индексы для определения сеточных значений функций. Момент времени разрушения обозначим через Tbl. Для начала сведем исходное уравнение (1) - (3) к системе первого порядка по времени. Это необходимо для применения эффективных численных методов, которые будут описаны ниже. Таким образом, задача1 ∂2 dt2 uxxx — zu — 2 u ) + uxx — 0, x G (0, l), t G (0,Tbi], u(x, 0) — Uinit0 (x), Ut (x, 0) — Uinit 1 (x), l dt2 / G“(x’t1 - Интегрируя равенство следующее равенство: l £ 2 \ d 2 Г / 1 \ 2 —u2(x,t) dx = 0 О u(x,t) — dx = 0. 2 dt2 J \ £ (31) по времени, с учетом начальных условий (3) получим l У uu(x,t)--^ dx = У ^u0(x)--^ dx + 2 tj Q u 1(x) dx. (32) Ux (0 ,t) — Ux (l,t) — 0 примет вид ∂ ∂t uxx ε22 — fU — -^ U ) —v, x G (0,l), t G (0, Tbl], ∂ — v + Uxx— 0, ∂t U(x, 0) = Uinit0 (x), v(x,0) — Uinit 1 (x)xx — ZUiniti (x) f Uinitо (x ) Uiniti (x ), чUx(0, t) Ux(l,t) 0•
5. Жесткий метод прямых и схема Розенброкас комплексным коэффициентом С целью численного решения системы (34) мы применяем жесткий метод прямых (SMOL) [6,7] для того, чтобы свести исходную систему уравнений в частных производных к неявной системе обыкновенных дифференциальных уравнений (к сожалению, не разрешенной относительно производных), которая может быть эффективно решена с помощью одностадийной схемы Розенброка с комплексным коэффициентом CROS1 [8]. Сначала мы введем равномерную сетку XN только по пространственной переменной x с шагом h — (l — 0)/N. содержащую N + 1 узлов (что с<^ответствует N интервалам): XN — {xn, 0 6 n 6 N : xn — 0 + nh}. Таким образом, после конечноразностной аппроксимации пространственных производных co вторым порядком точности в (34) мы получим следующую систему обыкновенных дифференциальных уравнений, из которой требуется определить N — 1 неизвестных функций un = un(t) = и(xn,t) (n — 1 ,N — 1, и0 и uN определяются из соотношений, заданных граничными усло- виями: и0 — 3и 1 - Vn = Vn (t) „ 4. 3 и 2. Un — 3 Un -1 — 3uN-2 ) и N — 1 вспомогательных функций = v(xn,t) (n — 1 ,N — 1, v0 и vN не входят в систему): / dun-1 dt dun - (2 + eh2 + e2h2un)dUn + dt un+1 - 2un + un-1 dun+1 dt - h vn, где dt h2 , un (°) uinitо (xn), Vn (°) - uinit 1 (xn+1) 2uinit 1(xn ) + uinit 1(xn-1) и о — ии 1 — u2, 3 Un — uN--1 ^^^^.^^^~“ uN-2. h2 _ euiniti (xn ) _ £ uinitо (xn ) uiniti (xn ), Эта система может быть переписана в виде М(и)dt —/(u), ^(0) — ininiti и—uu 1 u2 u3 . . . uN-1 v 1 v2 v3 . . . vN-1) . / —ff1 f2 f3 . . . f2n-2) T и Uinit — (и 1(0) и 2(0) и 3(0) ... Un -1(0) v 1(0) v 2(0) v 3(0) ... vn -1(0)) T. Вектор-функция / имеет следующую структуру: h2vn, если n — 1 ,N - 1. fn - h12 u2 2 u 1 + (3 u 1 _ 13u2 , если n - N. h2 un-N +2 _ 1 h2 _ 2un-N+1 + Un-N^ , 3uN-2) — 2uN-1 + uN-2^ , если если n n — N + 1, 2N - 3. — 2N - 2. а матричная функция М имеет следующие элементы: — (2 + eh2 + e2h2и 1), если n — 1- M Mn,n-1 - Mn,n+1 - остальные элементы — (2 + eh2 + e2h2un), если n — 2,N - 2. 1, _ 1, _ _ 1, (2 + eh2 + £2h2uN - 1), если если если n — 2,N - 2. n n + 1, +1, если если если n n n — N - 1. — N, 2N - 2. — N - 1. — 1- матрицы М равны нулю. — 2,N - 2. пз Для численного решения системы (36) мы будем использовать схему Розенбро-ка с комплексным коэффициентом (CROS1), которая является наилучшим выбором для решения задач такого рода по причине порядка точности этой схемы (O(т 1)), ее монотонности и устойчивости (L2) [9]. Важно отметить, что в случае постоянной матрицы М схема Розенброка с комплексным коэффициетом имеет порядок точности O(т2) [10, 11]. Неявная система обыкновенных дифференциальных уравнений с такой матрицей может быть получена, если в системе (34) ввести следующую вспомогательную переменную: w = uxx — zu — уu2' В этом случае мы получим неявную систему обыкновенных дифференциальных уравнений (подобную (35)) с постоянной (но вырожденной) матрицей, размерность которой будет в 3/2 раза больше исходной, что приведет к увеличению времени вычислений. Какой из этих подходов более эффективен с вычислительной точки зрения - открытый вопрос. Нашей же основной целью является демонстрация того, как можно численно диагностировать факт разрушения решения по времени и/или пространству, - таким образом, в данной работе мы не исследуем поднятый в этом замечании вопрос. Для того чтобы применить эту схему, мы введем равномерную сетку (также можно использовать и квазиравномерную сетку без каких-либо изменений в алгоритме) TM по t. которая имеет M + 1 узлов (то есть M интервалов): TM = {tm, 0 6 m 6 M : 0 = 10 После этого мы можем применить схему CROS1 для решения системы (36): ^(tm +1) 1t(tm) + (tm+1 tm) Re W , где w является решением системы M(u (tm 1 +i ) 2 (tm +1 tm )/и\^\ tm ) J W Здесь fu - якобиан, который для рассматриваемой системы имеет следующую структуру: ( fu ) n,n + N -1 (fu)n,n-N = h2, если n = 1 , N — 1. { — h2, если n = N +1, 2N — 3, [ — p + 312, если n = 2N - 2. ( fu ) n,n-N+2 { 342, если n = N. если n = N + 1, 2N — 3. 342, если n = 2N - 2. ~ 42 + 312, если n = N. — h2, если n = N + 1, 2N — 3. 2 h2 h2 , 2 h2 Другие компоненты матрицы fu в случае рассматриваемого уравнения равны нулю. Таким образом, матрица системы (37) состоит из четырех блоков размерности (N — 1) х (N — 1) (структура матрицы представлена на рис. 1). Этот факт дает возможность применить алгоритм решения СЛАУ, который найдет решение системы (37) за O(N) операций. Рис. 1. Структура матрицы СЛАУ (37)
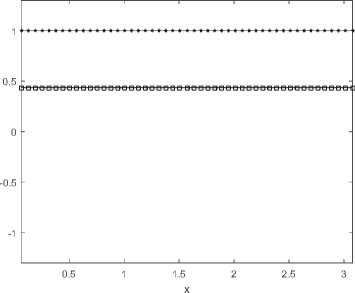
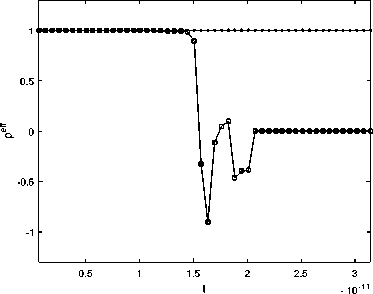
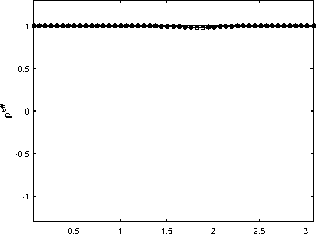
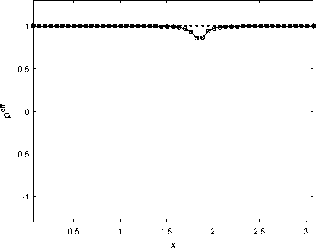
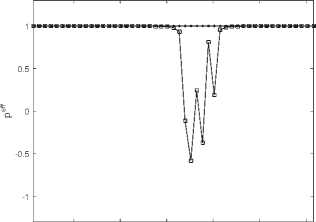
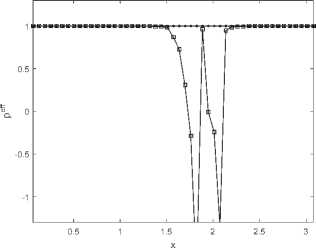
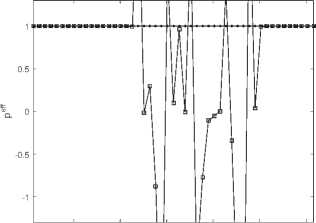
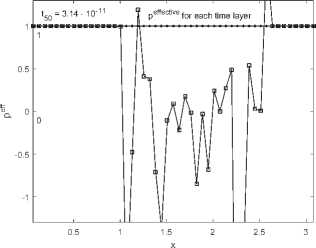
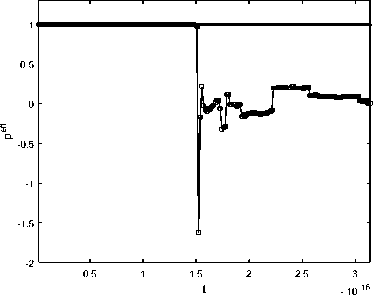
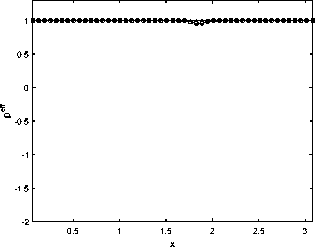
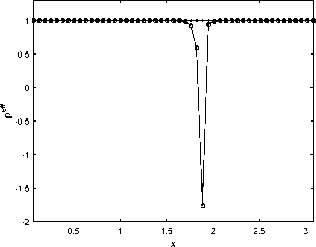
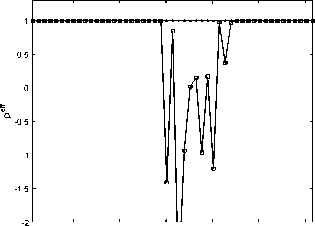
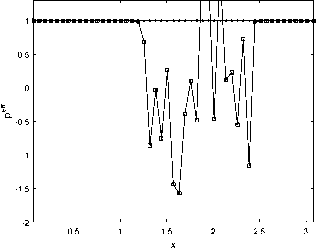
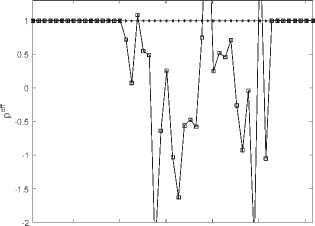
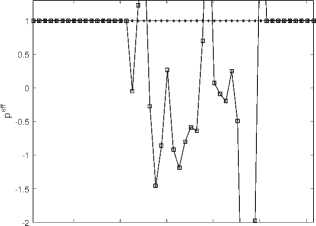
6. Вычисления на сгущающихся сетках При численных расчетах важно не только получить приближенный численный результат, но также и выполнить некоторую оценку его точности. Метод вычисления апостериорной асимптотически точной оценки погрешности [10] позволяет это сделать. Но этот метод также может помочь и диагностировать факт разрушения точного решения [11]. Основные формулы и утверждения этого параграфа впервые были представлены в работах [10-12]. Мы аппроксимировали все пространственные производные в (34) с точностью O(h2), а при численном интегрировании системы (36) используем схему CROS1, которая имеет точность O(т 1). Поэтому построенный метод решения системы (34) имеет точность O(т1 + h2). Для начала введем базовую сетку XN х TM: {xn, tm}, 0 6 n 6 N, 0 6 m 6 M. После этого произведем последовательное сгущение сетки, начиная с базовой, и вычислим решения u(x,t) на полученных сетках. В связи с тем, что теоретический порядок точности по времени равен 1, а по пространству 2, мы выполним последовательное сгущение сетки по времени в целое число раз rt и сгущение пространственной сетки в целое число раз rx так, чтобы выполнялось условие r1 = rX (подробности см. в [12]). Наиболее удобно для счета выбрать rt = 4 и rx = 2. В этом случае каждая последующая сетка Xrs-1N х Trs-1M (s - номер сетки) имеет узлы, совпадающие с узлами базовой сетки (xn,tm). В этих узлах (x,t) мы можем выполнить апостериорную асимптотически точную оценку погрешности [11,12] A(rs NrsM)( x,t) = u(rs NrtM)( x,t) — u(rs1 N,rt1M)( x,t) rt1— 1 + o (T1 + h2) и оценить эффективный порядок точности [11,12] Pesff(x,t) = logrt u(rs1Nrs1M) (x,t) — u(rs 2Nrs 2M)(x,t) -INrM^xt—Ur-Nr^ В точках (x,t), в которых решение исходной задачи имеет непрерывные первые производные по времени и вторые по пространству, имеет место сходимость Peff (X,t) -----> ptheor = 1, s→∞ и соответствующая оценка погрешности является асимптотически точной при s д то (или, что то же самое, N,M д то). Нарушение этой сходимости (38) говорит о потере гладкости точного решения. В частности, в случае степенной «сингулярности » и(x,t) ~ (t* — t)-в для любого t > t* эффективный порядок точности peff (x,t) ----д -в- Это позволяет нам найти соответствующую степень в- Ес-s→∞ ли peff(x,t) ---д —то для любого t > t*, мы можем утверждать, что решение s→∞ экспоненциально возрастает, т.е. и(x,t) д то; если peff(x,t) ----д 0 для любого s→∞ t > t*, то рост решения в окрестности «сингулярности» является логарифмическим: и(x,t) ~ ln(t* — t). Момент разрушения решения t* может быть найден с точностью до величины интервала базовой сетки по времени. Если нарушение гладкости решения возникает во всей области по пространственной переменной одновременно, то отклонение сходимости peff(x,t) от 1 возникает во всех точках сетки {xn} с первого временного слоя t > t* (см. Пример 1а). Если разрушение решения возникает в одной-единственной точке х*, то описанный метод позволяет проследить во времени процесс разрушения решения в остальных точках (см. Пример 16 и Пример 1в). Такая диагностика процесса разрушения решения возможна в связи с тем, что схема CROS не приводит к переполнению даже в том случае, если решение задачи устремляется к бесконечности [10,11]. Пример 1а. Для начала рассмотрим пример со следующим набором входных данных: Uinit0(х) = 0, им 1 (х) = — 1, l = п, е = 1. В данном случае решение уравнения (33) может быть найдено аналитически: и (x,t ) = д/1 — 21 — 1. (39) Очевидно, что в данном случае время разрушения равно Tbl = Т^ = 0,5. Кроме того, это подтверждается непосредственно формулой (29). Применим численный алгоритм диагностики момента и места разрушения решения, а заодно и сверим получившиеся результаты с аналитическими расчетами. Для численного решения задачи (33) мы возьмем следующий набор параметров: Т^ = 0, 5, N = 50, M = 200, rx = 2, rt = 4, S = 6 (число последовательно используемых для вычислений сеток, включая начальную). Получив приближенное численное решение на разных сетках, мы можем проверить сходимость эффективного порядка точности к теоретическому для каждого временного слоя по формуле peff (tm ) = lOgrt ^N=;^U(rдrs-1M)"д6-^дrs-2M)"дд)^ JYNHUNMX^ где s - номер соответствующей сетки. Также еще раз хотим обратить внимание, что под обозначением (xn,tm) подразумеваются узлы, совпадающие с соответствующими узлами базовой сетки. После вычислений на S вложенных сетках эффективный порядок точности p eff для каждого в ременного слоя tm сходится к ptheor = 1 (см. рис. 2) за исключением временного слоя, соответствующего моменту времени 1200: peff(1200) д 0, 5. что озиачает, что Tbi G (1199,t200] = (0, 498, 0, 5] является временем разрушения решения, и что в точке Ты решение имеет степенной характер роста и(x,t) ~ (Tbi — t)0’5. Мы также можем оценить эффективный порядок точности для каждой пространственной точки выбранного временного слоя, соответствующего моменту времени tm, по формуле (rS-1N,rS-1M) (rS-2N,rt-2M) Peff (xn,tm ) = logrt u (xn, m) u (xn, m) -xNrMwn^tmi-ur-^ Можно использовать эту формулу, например, для временного слоя, соответствующего моменту времени 1200, в котором было диагностировано разрушение решения, с целью определить, возникло ли разрушение на всем временном слое или только в отдельных точках по пространственной переменной. На рис. 3 мы можем видеть, что решение разрушилось во всех пространственных точках соответствующего временного слоя. Тем не менее, как мы видим на рис. 2, «точной» сходи мости peff к 0,5 нет. В данном случае этого можно добиться, увеличив число сеток S, на которых будут выполняться вычисления. 0.5 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5 t Рис. 2. Пример 1а. Эффективный порядок точности для каждого временного слоя. Разрушение решения диагностировано в момент времени Ты Е (1199,t200] = (0,498, 0,5]. Здесь и далее нулевой временной слой не показан Рис. 3. Пример 1а. Эффективный порядок точности для каждой пространственной точки временного слоя, соответствующего моменту времени 1200 = 0, 5, на котором был диагностирован факт разрушения решения. Разрушение решения диагностировано во всех пространственных точках этого временного слоя Пример 16. Рассмотрим пример со следующим набором данных: uinit0(x) = 0, unit 1 (x) = — (x(n — x))2 sin 3, l = п, e = 1010. В данном случае решение уравнения (33) уже не может быть найдено аналитически. Для численной диагностики разрушения решения во времени и в пространстве опять применим описанный алгоритм. Верхняя оценка T^ для времени разрушения Tbi может быть вычислена по формуле (29): Т^ ~ 3.14 • 10- 11. Для численного решения задачи (33) мы будем использвать следующий набор параметров: Т^ = 3, 14 • 10- 11, N = 50, M = 50, rx = 2, rt = 4, S = 5 (число сеток, использовавшихся для вычислений, включая исходную). Так же, как и в Примере 1а, мы можем оценить эффективный порядок точности по формуле (40). После вычислений на S вложенных сетках эффективный порядок точности p eff для каждого временного слоя tm сходится к ptheor = 1 (см. рис. 4) до временного слоя, соответствующего моменту времени 125. Это означает, что Tbl Е (124,t25] = (1,44, 1, 51] • 10-11 является временем разрушения решения. Мы также можем использовать формулу (41) для временного слоя, который соответствует моменту времени 125 и на котором было диагностировано разрушение решения, с целью определить, возникло ли разрушение на всем временном слое или только в отдельных точках по пространственной переменной. На рис. 5 мы можем видеть, что решение разрушается в одной пространственной точке соответствующего временного слоя, а затем взрыв распространяется постепенно на остальные точки отрезка. Рис. 4. Пример 16. Эффективный порядок точности для каждого временного слоя. Разрушение решения диагностировано в точке Tbl Е (124,t25] = (1,44, 1, 51] • 10-11 Пример 1в. Рассмотрим теперь аналогичную Примеру 16 задачу, но с более большим е: uinit0(x) = 0, uinit 1 (x) = — (x(n — x))2 sin 3, l = п, E = 1015. В этом случае решение уравнения (33) также не может быть найдено аналитически. Применим вновь описанный выше алгоритм для разрушения решения во времени и в пространстве. Верхнюю оценку Тж для времени разрушения Tbl вычисляем по формуле (29): T^ ^ 3, 14 • 10- 16. Для численного решения задачи (33) мы будем использвать следующий набор параметров: T^ = 3, 14 • 10- 16, N = 50, M = 200, rx = 2, rt = 4, S = 5 (число сеток, использовавшихся для вычислений, включая исходную). Так же, как и в предыдущих двух примерах, мы можем оценить эффективный порядок точности по формуле (40). После вычислений на S вложенных сетках эффективный порядок точности peff для каждого в ременного слоя tm сходи тся к ptheor = 1 (см. рис. 6) до временного слоя, соответствующего моменту времени 198. Это означает, что Tb)l Е (197,t98] = (1,51, 1, 52] • 10-16 является временем разрушения решения. Используем формулу (41) для временного слоя, который соответствует моменту 0.5 1 1.5 2 2.5 3 0.5 1 1.5 2 2.5 3 Рис. 5. Пример 16. Эффективный порядок точности для каждой пространственной точки для временных слоев (t24,t25,t26,t27,t28,t39,t50). Здесь мы видим, что сначала разрушение происходит в одной пространственной точке, а потом оно распространяется на остальные точки отрезка Рис. 6. Пример 1в. Эффективный порядок точности для каждого временного слоя. Разрушение решения диагностировано в точке Ты Е (t97,t98] = (1, 51,1,52] • 10-16 времени t98 и на котором было диагностировано разрушение решения, с целью определить, возникло ли разрушение на всем временном слое или только в отдельных точках по пространственной переменной. На рис. 7 мы можем видеть, что решение разрушается в одной пространственной точке соответствующего временного слоя, а затем взрыв распространяется постепенно на остальные точки отрезка. Рис. 7. Пример 1в. Эффективный порядок точности для каждой пространственной точки для временных слоев (t97,t98,t110,t150,t180,t200). Здесь мы видим, что сначала разрушение происходит в одной пространственной точке, а потом оно распространяется на остальные точки отрезка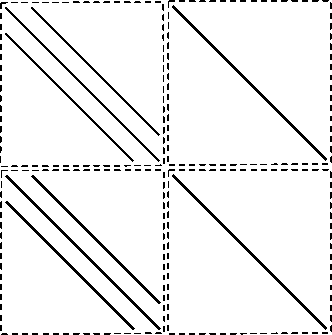

Список литературы Локальная разрешимость и разрушение решения одного уравнения с квадратичной некоэрцитивной нелинейностью
- Корпусов, М.О. Критические показатели мгновенного разрушения или локальной разрешимости нелинейных уравнений соболевского типа/М.О. Корпусов//Известия РАН. Серия математическая. -2015. -Т. 79, № 5. -C. 103-162.
- Korpusov, M.O. Blow-up for One Sobolev Problem: Theoretical Approach and Numerical Analysis/M.O. Korpusov, D.V. Lukyanenko, A.A. Panin, E.V. Yushkov//Journal of Mathematical Analysis and Applications. -2016. -V. 442, № 2. -P. 451-468.
- Korpusov, M.O. Blow-up Phenomena in the Model of a Space Charge Stratification in Semiconductors: Analytical and Numerical Analysis/M.O. Korpusov, D.V. Lukyanenko, A.A. Panin, E.V. Yushkov//Mathematical Methods in the Applied Sciences. -2017. -V. 40, № 7. -P. 2336-2346.
- Корпусов, М.О. О разрушении за конечное время решения начально-краевой задачи для нелинейного уравнения ионно-звуковых волн/М.О. Корпусов//Теоретическая и математическая физика. -2016. -Т. 187, № 3. -C. 447-454.
- Панин, А.А. О локальной разрешимости и разрушении решения абстрактного нелинейного интегрального уравнения Вольтерра/А.А. Панин//Математические заметки. -2015. -Т. 97, № 6. -C. 884-903.
- Hairer, E. Solving of Ordinary Differential Equations/E. Hairer, G. Wanner. -Berlin; Heidelberg: Spinger-Verlag, 2002.
- Калиткин, Н.Н. Численные методы решения жестких систем/Н.Н. Калиткин//Математическое моделирование. -1995. -Т. 7, № 5. -С. 8-11.
- Rosenbrock, H.H. Some General Implicit Processes for the Numerical Solution of Differential Equations/H.H. Rosenbrock//The Computer Journal. -1963. -V. 5, № 4. -P. 329-330.
- Альшин, А.Б. Схемы Розенброка с комплексными коэффициентами для жестких и дифференциально-алгебраических систем/А.Б. Альшин, Е.А. Альшина, Н.Н. Калиткин, А.Б. Корягина//Журнал вычислительной математики и математической физики. -2006. -Т. 46, № 8. -C. 1392-1414.
- Альшина, Е.А. Диагностика особенностей точного решения при расчетах с контролем точности/Е.А. Альшина, Н.Н. Калиткин, П.В. Корякин//Журнал вычислительной математики и математической физики. -2005. -Т. 45, № 10. -C. 1837-1847.
- Al'shin A.B. Numerical Diagnosis of Blow-up of Solutions of Pseudoparabolic Equations/A.B. Al'shin, E.A. Al'shina//Journal of Mathematical Sciences. -2008. -V. 148, № 1. -C. 143-162.
- Вычисления на квазиравномерных сетках/Н.Н. Калиткин, А.Б. Альшин, Е.А. Альшина, Б.В. Рогов. -М.: Физматлит, 2005.


