Магнитный момент квантового цилиндра со сверхрешеткой

(Работа поддержана грантом регионального конкурса ABO-РФФИ «Поволжье» 04-02-96505)

Исследования магнитного отклика различных низкоразмерных систем доставляют важную информацию об электронном энергетическом спектре и потенциале латерального конфайнмента в этих структурах [3; 6; 8]. Приложенное к наноструктуре магнитное поле может создавать дополнительный или усиливать имеющийся латеральный конфайнмент в наноструктуре, а также создавать гибридную связь движений вдоль и поперек поля в случае, когда поле направлено под углом по отношению к оси симметрии системы [3].

Магнитный отклик наноструктур с цилиндрической симметрией при Т = 0 ( Т - температура) изучался в [8] для случая слабого магнитного поля, которое рассматривалось как возмущение. В [3; 6] теоретически исследовался магнитный отклик свернутого в цилиндр двумерного вырожденного электронного газа в постоянном и однородном магнитном поле, параллельном оси цилиндра. В [2] было получено выражение для момента квазиодномерной сверхструктуры в наклонном магнитном поле.

В настоящее время развитие нанотехнологий сделало возможным изготовление из слоев напряженного GaAs/GaAlAs поверхностей различной кривизны [7], в том числе цилиндрических, обладающих необычными физическими свойствами [3]. Особое внимание исследователей уделяется квантовым наноструктурам, конфайнмент которых можно моделировать параболическим потенциалом [1].

Цель настоящей работы — теоретическое исследование магнитного отклика свернутого в цилиндр двумерного вырожденного электронного газа (квантовый цилиндр) со сверхструктурой в постоянном и однородном магнитном поле В, параллельном оси цилиндра. Показано, что зависимость наведенного магнитного момента от потока магнитного поля имеет осцилляционный характер.

Равновесные свойства электронного газа в наноструктурах в основном определяются электронным энергетическим спектром, который, в свою очередь, обусловлен геометрией системы [6].

Для квантового цилиндра со сверхрешеткой в приближении эффективной массы гамильтониан Н одноэлектронных бесспиновых состояний для векторного потенциала А, выбранного в виде А = (Ду/2 — Дх/2,0), в цилиндрических координатах запишется в виде d" ihco,. d    m*о" i ( nd A

H - - O ---1--₊ -----L. p- ₊ Д [ _ _cos £_  / ] X

2            2 V                             ¹

где toc = eS / me- циклотронная частота, ф - полярный угол, m* - эффективная масса электрона, р - импульс вдоль оси цилиндра, 8 = fi2/2т р2 - энергия размерного конфайнмента, р - радиус цилиндра, д - полуширина мини-зоны, d - период сверхрешетки.

Спектр гамильтониана (1) имеет вид

( Ф )

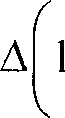
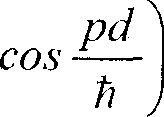
е тр

I Фо)

В (2) магнитное квантовое число т принимает значения т = 0, ±1,±2,..., поток поля В через сечение цилиндра ф = кр²В, Ф_о = hc/\e\ - квант потока. Воспользовавшись формулой (1) из [6], найдем наведенный магнитный момент по формуле

М _ Lm₀    ”г (ш + Ф/Ф₀)<ф>

Ив тАт*    j 1 + ехр[8тр - д/Т] ’ где /и0 - масса свободного электрона, рв - магнетон Бора, L - длина канала.

ИЗВЕСТИЯ ВГПУ

Далее воспользуемся формулой суммирования Пуассона [5]. После несложных преобразований получим

--= LCvM)sw 17rv"^~

Рв r=i          \ Фо.

о 7

где коэффициенты Фурье С (7) имеют вид сА*^ л Tim

^zsin(vz)dz J dp l + exp

о

о

Введем новые переменные: b = p,2N - sz"^л¹ \ , х = pd]2ti и учтем, что МД-со$2х)= =2\sin²x. При этом получим для С (7) выражение

2Lm0 ( n2dm* *

о

sin" x-b T

Для качественного исследования характера зависимости магнитного момента от потока магнитного поля рассмотрим случай, когда 7'= 0. В этом случае подынтегральный член (1 + ехДуш2 х-б/Т'])"' приобретает вид ©^sin2 X - б), где 0(х) - тэта-функция. Тогда

С(0) можно записать так:

2Lm0 [ л2 dm* *

о

В случае, когда // / 2 А < 1, получим для С (0)

сАоУ-^А л dm

м(т = о)

риМй

При // / 2 А >  1

м^т = о) цвМ0

О

= ^sin 2лу

имеем

2Lm0

K^dm

= У sin 2лу-- ф

>-I V ^0 .

'arcsin J---- —dz ,

V 2Д 8л-А

ф

Фп

о

. P EZ" \arcsmA---:—

V 2A 8zr2A

Prcsm 1----—dz

V2A 8tt²A

. p EZ" , Prcsm,--- 7— dz

V 2A 8tt²A

2^

(Ю)

(Н)

где обозначено Mo=2Lmdudm . Для реальных ситуаций обычно выполняется д>>£. Кроме того, из (11) видно, что достаточно провести исследование осцилляций в области, где 0 < Ф/Ф_о< 1. Отметим, что интегралы в (8) и (10) не выражаются через табулированные функции.

Дальнейший анализ зависимости наведенного магнитного момента от потока магнитного поля проведем с помощью типичных параметров: m₀ = т*=10²⁹ г, А =0.01 эВ, L = 2лр, р = 5 40'⁶ см, =10⁶ см.

График зависимости наведенного магнитного момента квантового цилиндра от потока магнитного поля для первого случая представлен на рис. (а), для второго - на рис. (б) Сравнивая графики зависимости магнитного момента квантового цилиндра с графиками, приведенными в [1], представленными на рисунке, видим появление дополнительных осцилляций, которые можно объяснить наличием дополнительного периодического потенциала сверхрешетки.

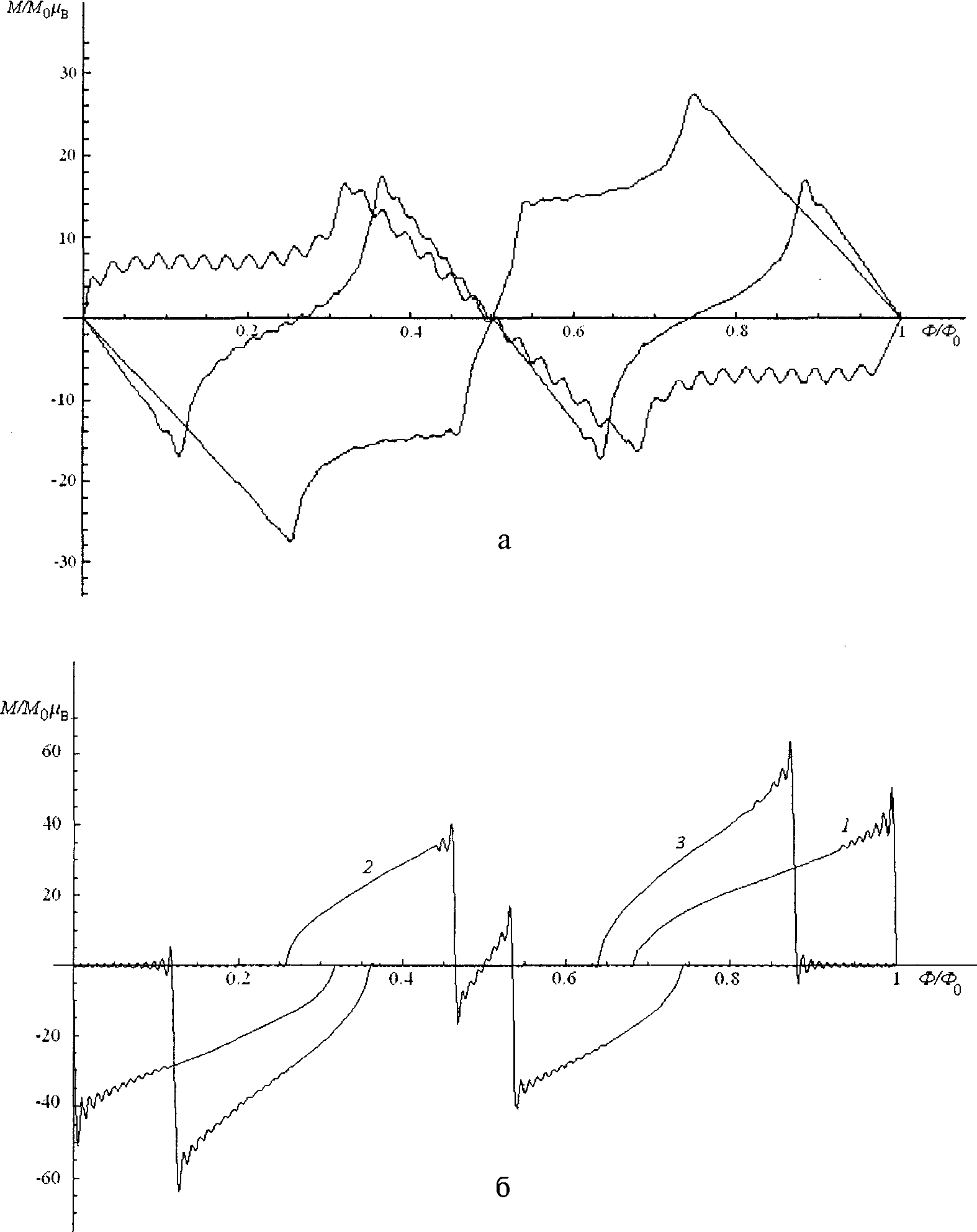
Зависимость наведенного магнитного момента квантового цилиндра со сверхструктурой от потока магнитного поля. Кривая 1 соответствует случаю, когда соотношение ц/е = 11, кривая 2 — 14 и кривая 3 — 19

ИЗВЕСТИЯ ВГПУ