Математическая модель дизель-генератора переменного тока со статической нагрузкой

Эксплуатация надводных кораблей и неатомных подводных лодок в современных условиях сопряжена с необходимостью нивелирования противоречия между максимально полным использованием имеющихся в наличии кораблей и необходимостью сбережения имеющегося ресурса технических средств [1-3]. В этих условиях процедуры технического диагностирования становятся необходимым условием обеспечения надежной эксплуатации энергетической установки корабля [4, 5].

Техническое диагностирование дизель-генераторной установки позволяет определять оптимальные сроки технического обслуживания и ремонта в соответствии с объективным фактическим состоянием технических средств и учетом директивных ограничений, которые определяются нормами эксплуатации и ремонта оборудования [6, 7]. Встроенные средства контроля технического состояния энергетического оборудования в большей степени ориентированы на предупреждение аварийных ситуаций, а не на диагностирование состояния объектов [8]. Поэтому для углубленного технического диагностирования на борту надводных кораблей и неатомных подводных лодок целесообразно использовать переносные диагностические комплексы, реализующие современные методологические подходы, основанные на применении цифровых технологий. Переносной диагностический комплекс должен включать необходимые измерительные приборы, датчики и программное обеспечение сбора и обработки информации [9, 10]. Но ключевым его

Одинаев В.А., Шигапов И.И., Математическая модель дизель-генератора Долгов В.А., Саськов К.Г. переменного тока со статической нагрузкой элементом должна быть математическая модель дизель-генератора, учитывающая условия его эксплуатации, техническое состояние и влияние внешних условий.

Целью исследования являлась разработка математической модели дизель-генератора переменного тока со статической нагрузкой неатомной подводной лодки типа 28ДГ, состоящего из корабельного дизеля 8ЧН26/26 и генератора СБГД-1000. Отличительная особенность этого ди-зель-генератора состоит в том, что, выступая на корабле в качестве источника постоянного тока, генератор одновременно является синхронной электрической машиной, которая работает на выпрямитель.

Математическая модель дизель-генератора

Имитация функционирования приводного дизеля 8ЧН26/26 из состава дизель-генераторной установки осуществляется на основе агрегированной базовой математической модели функционирования корабельного двигателя внутреннего сгорания (БММ), разработанной коллективом научной школы профессора П.М. Гацака [11, 12]. В основе модели лежит аналитическое описание влияния на параметры функционирования корабельных дизелей не только факторов режима (сочетание частоты вращения коленчатого вала и эффективной мощности), но и параметров внешних условий (барометрическое давление, температура и относительная влажность атмосферного воздуха, температура забортной воды), технического состояния и регулировки отдельных элементов, влияющих на воздухоснабжение, газообмен, индикаторные процессы, механические потери и др. Такая математическая модель успешно применяется в научных исследованиях [12].

Основной особенностью БММ функционирования двух- и четырехтактных двигателей внутреннего сгорания (ДВС) с различными схемами воздухоснабжения на установившихся и неуста-новившихся режимах является ее целевая функция - поиск точки совместной работы всех агрегатов дизеля, т. е. нахождение такого количества воздуха, прошедшего через газовоздушный тракт дизеля, которое удовлетворяет всем заданным условиям (параметров режима, внешних (атмосферных) условий, технического состояния и регулировки). В качестве критерия сходимости та- ких итерационных расчетов с заданной точностью грв принято условие [11]:

G V 0 - G ВЫХ G ВЫХ

— £(  ,

G _В

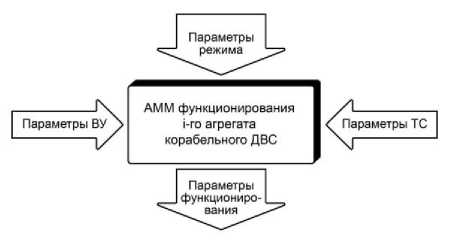
Рис. 1. Схема автономной математической модели агрегата ДВС (АММ – совокупность автономных математических моделей, ВУ – внешние условия, ТС – техническое состояние)

^{где G}ВЫХ = ^GГЦ + G yT   G T .

Агрегированная БММ состоит из совокупности автономных математических моделей (АММ) агрегатов дизеля, представляющих собой совокупность алгебраических, трансцендентных, регрессионных уравнений и различных функциональных ограничений. Существующие между автономными моделями отдельных агрегатов прямые и обратные функциональные связи реализуются в основной управляющей модели.

В автономных математических моделях агрегатов используются известные уравнения из теории ДВС, а также зависимости, описывающие индикаторные процессы, газообмен, составляющие механических потерь, показатели агрегатов турбонаддува и т. д., полученные за последние десятилетия [11–16]. Схема автономной математической модели агрегата ДВС представлена на рис. 1.

Основная задача частной математической модели «Отдельный цилиндр ДВС» сводится к вы- числению численных значений основных и дополнительных переменных, которые соответствуют реальному объекту при поддержании постоянными идентичных входных (основных и дополнительных) характеристик. К основным характеристикам относятся параметры газа на выходе из цилиндров дизеля (давления, температуры Тгц, газовой постоянной R^ и массового расхода GГц).

Одним из самых сложных трансцендентных уравнений частной математической модели «Отдельный цилиндр ДВС» является выражение для определения среднемассовой температуры газовоздушной смеси на выходе цилиндра [11]:

Математика

Т гц = L о • а С • G t • 0,24 • ( Т кц - 273) - G yT ^Z • 0,24 • (Т срУТ - 273) + 0,445 • G k • ( Т кц - 273) +

+

Hu^GrJl -ni-Z cm- Cs^ N™ '^^

0,228 + 1,64 - 10 - ² a c

+

^ 2,625 - 10 — ⁵ + 6 - 10 — ⁶ ^

a c

• ^ТГЦ

4,18 •

ч RT* - 1 1 - 0,18 ) 29,3

+ 273.

^a £ c  J

• ^GГЦ

Газовая постоянная R ГЦ на выходе из цилиндра определяется с помощью известного выражения [11], а массовый расход газа через поршневую часть двигателя определяется как

GГЦ = Gvy + GT, где Gvц – массовый расход воздуха после выпадения конденсата в воздухоохладителе, кг/ч. Из дополнительных выходных переменных оценка часового расхода топлива Gт кг/ч может быть определена по формуле [4]:

G _T = 632,3-- ^e— ,

Hu • n e

Рис. 2. Структурная схема математической модели функционирования корабельного ДВС с осреднённой поршневой частью

где n _e — эффективный КПД двигателя вычисляется как произведение механического КПД п м и индикаторного КПД n i , ^т - е. П е = П _м • n i , при этом, механический КПД определяется как П м = Ne / N i' , а индикаторный КПД - с помощью произведения относительных сомножителей, полученных в результате натурных и расчетно-экспериментальных исследований [5, 11, 12, 17–19]:

П і = П іб • П т • ⁿ ia • П л • ⁿi _£ • ⁿZ _cm • ^Піп _д • ⁿir • ⁿiG k ^-П

В свою очередь индикаторная мощность двигателя N i , кВт, определяется по формуле

• 1     e ⁺ трд     нх      тк '

Принципиальным моментом БММ является ее инвариантность к типу главной энергетической установки или к проекту корабля. Универсальность БММ обеспечивается возможностью ее настройки применительно к заданной версии или типу двигателя и проверяется сравнением расчетов на БММ функционирования ДВС с соответствующими результатами стендовых заводских или корабельных испытаний.

Версии агрегированной БММ для приводного дизеля 8ЧН26/26 позволяют адекватно моделировать рабочие процессы в «осредненной» поршневой части, «развернутой» по отдельным блокам и цилиндрам, а также учитывают особенности схем воздухоснабже-ния, газоотвода и др. Эти требования выполняются уже на этапе формирования структуры версии БММ функционирования среднеоборотных ДВС размерности 26/26.

Топологическая структурная схема математической модели функционирования корабельного ДВС с осреднённой поршневой частью, приведенная на рис. 2, состоит из шести моделей-модулей: впускного устройства VPU 1; компрессора COMPR 2; воздухоохладителя CLV 3; осредненной поршневой части двигателя CLND 4 с включенным в него механизмом изменения угла опережения подачи топлива; осредненного выпускного коллектора VIPK 5; газовой турбины TURB 6. Каждый модуль имеет четыре типа перемен ных (два типа входных и два типа выходных переменных). Схема математической модели i-го модуля дизеля аналогична представленной на рис. 2, то есть V0, V1 , V2, V3, V4, V5, V6 – входные и выходные параметры воздуха (газа); Z11 … Z13, Z21 … Z27, Z31 … Z36, Z41 … Z437, Z51 … Z59, Z61 … Z68 – дополнительные входные переменные, характеризующие параметры нагрузки, технического состояния, конструктивные данные, внешние условия; P21…P27, P31, P41…P450, P61…P64 – дополнительные выходные переменные, характеризующие параметры

Одинаев В.А., Шигапов И.И., Долгов В.А., Саськов К.Г.

Математическая модель дизель-генератора переменного тока со статической нагрузкой рабочего процесса каждого агрегата. Некоторые выходные параметры функционирования ДВС являются диагностическими параметрами. Для определения выходных параметров используются соответствующие математические зависимости из исходной математической модели функциони- рования корабельного ДВС.

Структурная схема (см. рис. 2) в полном объеме обеспечивает решение параметрического диагностирования газовоздушного тракта (ГВТ) дизеля 8ЧН26/26 в составе ди-зель-генераторной установки ДГУ-28ДГ, но накладывает ограничение на её применение для моделирования рабочих процессов с дифференциацией по блокам и отдельным цилиндрам двигателя.

Для обеспечения задачи углубленного диагностирования блоков и цилиндров дизеля используется математическая модель функционирования корабельного ДВС 8ЧН26/26 с дифференциацией рабочих процессов по i -му блоку и j -му цилиндру.

Топологическая структурная схема математической модели приведена на рис. 3. Моделирование многоцилиндровой поршневой части производится в результате многократного обращения к математической модели отдельного i -го цилиндра, включения прямых и обратных связей между математическими моделями других агрегатов ДВС, а также определения точки совместной работы всех агрегатов ДВС по массовому расходу

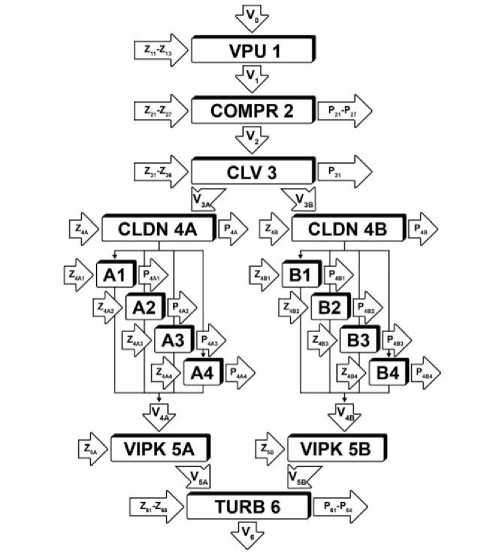
Рис. 3. Топологическая структурная схема математической модели корабельного ДВС с дифференциацией рабочих процессов по блокам и цилиндрам применительно к дизелю 8ЧН26/26

воздуха.

В представленной на рис. 3 топологической структурной схеме: А1...A4, B1…B4 – модели отдельного цилиндра в i -м блоке главного двигателя; V3A, V3B, V4A, V4B – входные и выходные параметры воздуха (газа) осредненной по i -му блоку поршневой части двигателя; V3A1...V3A4, V3B1...V3B4 – параметры воздуха на входе в каждый цилиндр i -го блока; V4A1...V4A4, V4B1...V4B4 – параметры газа на выходе из каждого цилиндра i -го блока; Z3A1...Z3A4, Z3B1...Z3B4 – дополнительные входные переменные для каждого цилиндра, характеризующие параметры нагрузки, технического состояния, конструктивные данные, внешние условия; P3A1...P3A4, P3B1...P3B4 – дополнительные выходные переменные, характеризующие параметры рабочего процесса в каждом цилиндре.

Математическая модель синхронного генератора

Генератор представляет собой шестифазную синхронную машину с бесконтактным возбуждением. На статоре размещены две трехфазные обмотки, соединенные по схеме «звезда», которые сдвинуты относительно друг друга на 30°, с изолированной нейтралью. Выходы каждой обмотки подключены к трехфазному выпрямителю по схеме Ларионова (рис. 4). L

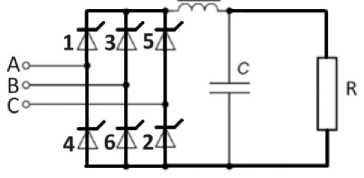
Рис. 4. Выпрямитель, подключенный к клеммам А, В, С трёхфазной обмотки статора (А, В, С – клеммы трёхфазной обмотки статора, R – нагрузка, LC – сглаживающий фильтр на выходе выпрямителя, L – индуктивность, С – ёмкость)

При математическом моделировании приняты следующие допущения ввиду незначительности их влияния на моделируемые процессы: потери в стали (явления гистерезиса и вихревые токи) не

Математика

учитываются; насыщение магнитопровода не учитывается; считается, что воздушный зазор между телом ротора и статором неизменный, как и магнитная проводимость; высшие пространственные гармоники магнитного поля не учитываются, то есть распределение магнитного поля каждой из обмоток вдоль окружности ротора и статора принято синусоидальным; статор имеет симметричные трехфазные обмотки.

Математическая модель генератора реализуется системой дифференциальных уравнений [20, 21] с учетом влияния взаимной индуктивности между обмотками. Уравнения потокосцеплений для первой обмотки статора (первой «звезды») имеют следующий вид:

ш. = L .I,+ m  i + m  i,+ m   i,+ m  i,, + m  i,+ mi a 1       a 1 a 1       a 1 b 1 b 1       a 1 c 1 c 1       a 1 a 2 a 2       a 1 b 2 b 2       a 1 c 2 c 2       a 1 fdfd

• w,. = LI + m  i.+ m  i.+ m  i,+ m  i., + m  i,+ mi

r b 1       b 1 b1       b1 a 1 a 1       b1 c 1 c 1       b 1 a 2 a 2       b 1 b 2 b 2       b 1 c 2 c 2       b1 fdfd

• w. = L .I.+ m  i + m  i.+ m  i,+ m  i,,+ m  i,+ mi

t c 1       c 1  c 1       c 1 b 1 b 1        c 1 a 1 a 1        c 1 a 2 a 2        c 1 b 2 b 2        c 1 c 2 c 2        c 1 fdfd где w — потокосцепление обмотки; индексы 1, 2 - номер «звезды»; i - ток фазы; L - собственная индуктивность обмотки; m - взаимная индуктивность между обмотками с соответствующими индексами; f - символ обмотки возбуждения; d - символ продольной оси ротора.

Уравнения потокосцеплений y a ₂ , y_{b 2} , y_{c 2} для второй обмотки статора (второй «звезды») записываются аналогично. Уравнение потокосцепления обмотки возбуждения имеет вид:

Wfd = LfdIfd + mfda 1 ia 1 + mfdb1 ib 1 + mfdc 1 ic 1 + mfda2 ia2 + mfdb2 ib2 + mfdc2 ic2 , а система уравнений синхронного генератора имеет следующий вид:

_ dWa 1 _» Ra 1 dt Ia1 = Ul  - d^a^ - R2 ■ I2 a1                      a 2    a 2 dt = ua 2 _ dWb 1 Rb1' dt Ib1 d' U b 1,         ,      Rb 2  Ib 2 dt =ub 2, dWc 1   „ ---R^ ‘ dt Ic1 = U - W - R^ c1                       c 2    c 2 dt =uc 2, w+'d'R dt rd dw„ = 0,    . + I^Rq = 0, dt dw f —f-+If' Rf dt      f    f 2 u f, J —Y = M - M, f       dt2      м где U - напряжение в фазе обмотки статора; I - ток фазы обмотки статора; R - сопротивление фазы обмотки статора; rd - символ демпферной обмотки ротора, расположенной по его продольной оси d; rq - символ демпферной обмотки ротора, расположенной по его поперечной оси q; ү -угол поворота ротора, радиан; dY/dt - синхронная скорость вращения ротора и магнитного поля машины, равная rns; d2ү/dt2 - ускорение ротора; Мм - крутящий (вращающий) момент дизеля; М -электромагнитный момент (момент сопротивления) генератора.

Каждая «звезда» генератора работает непосредственно на мощный выпрямитель, выполненный по схеме Ларионова (см. рис. 4). В процессе математического моделирования вентили выпрямителя представляются в схеме замещения сопротивлениями R VD в прямом и бесконечно большим сопротивлением в обратном направлениях. Звено выпрямителя рассматривается совместно со схемой замещения [21] одной «звезды» синхронного генератора (рис. 5).

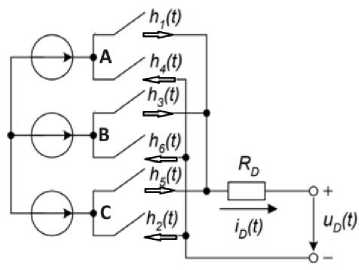
Рис. 5. Звено выпрямителя совместно со схемой замещения одной «звезды» статора: ( h 1 (t), h 2 (t), h 3 (t), h 4 (t), h 5 (t), h_s(t) - ключи, эквивалентные состоянию вентиля [0>закрыт, 1>открыт]; i_D(t) - выпрямленный ток; u_D(t) - выпрямленное напряжение; R_D= 2 R_VD, стрелки – направление тока, протекающего через каждый вентиль)

Нумерация вентилей соответствует порядку их включения в схеме Ларионова. Открытие вентиля происходит в небольшом промежутке времени, когда на нём действует прямое напряжение.

Одинаев В.А., Шигапов И.И., Математическая модель дизель-генератора Долгов В.А., Саськов К.Г. переменного тока со статической нагрузкой В этом промежутке подаётся импульс на управляющий электрод S (если это тиристор) или напряжение на открытие затвора G (если это транзистор IGBT). Закрытие вентиля происходит, когда напряжение на нём меняется с прямого на обратное.

Временной график функционирования выпрямителей представлен на рис. 6. Здесь столбцы, помеченные VZ1, относятся к первой «звезде» и к первому выпрямителю, а столбцы, помеченные VZ2 – ко второй «звезде» и ко второму выпрямителю; l 1 ( t ) , l 2 ( t ) , l 3 ( t ) , l 4 ( t ) , l 5 ( t ) , l 6 ( t ) – промежутки времени, в которые подаются импульсы на открытие вентилей первого выпрямителя; k 1 ( t ) , k 2 ( t ) , k 3 ( t ) , k 4 ( t ) , k 5 ( t ) , k 6 ( t ) – промежутки времени, в которые подаются импульсы на открытие вентилей первого выпрямителя; Т = 360° – период синусоиды напряжения (физически это 10 мс при частоте тока 100 Гц).

В нижней части рис. 6 представлен график выпрямленного напряжения (без учета действия сглаживающего фильтра). Таким образом, в генераторной установке используется двенадцати-пульсная система выпрямления переменного тока.

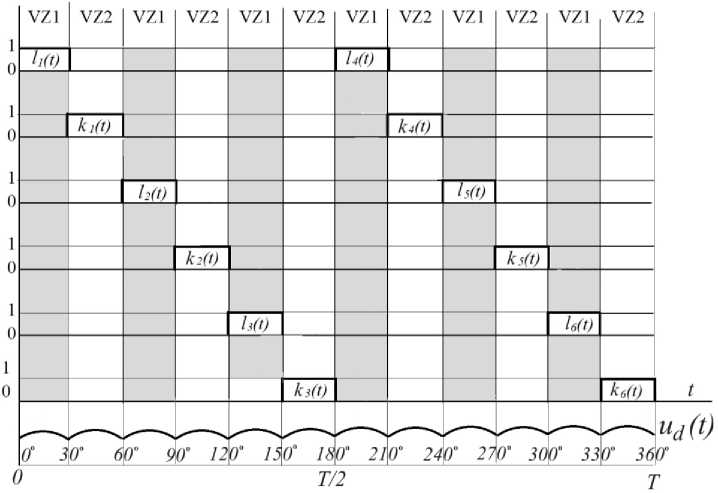
Рис. 6. Промежутки времени, в которые подаются импульсы на открытие вентилей; выпрямленное напряжение u D ( t ) на протяжении одного периода синусоиды Т = 360° (10 мс)

Направления тока и замкнутые ключи в течение одного периода синусоиды Т = 360º (10 мс)

Фрагмент синусоиды	Направление тока	Замкнутые ключи
От 0° до 30°	От клеммы А 1 к клемме В 1	h 1 и h 6 первого выпрямителя
От 30° до 60°	От клеммы А 2 к клемме В 2	h 1 и h 6 второго выпрямителя
От 60° до 90°	От клеммы А 1 к клемме С 1	h 1 и h 2 первого выпрямителя
От 90° до 120°	От клеммы А 2 к клемме С 2	h 1 и h 2 второго выпрямителя
От 120° до 150°	От клеммы B 1 к клемме C 1	h 3 и h 2 первого выпрямителя
От 150° до 180°	От клеммы B 2 к клемме C 2	h 3 и h 2 второго выпрямителя
От 180° до 210°	От клеммы B 1 к клемме A 1	h 3 и h 4 первого выпрямителя
От 210° до 240°	От клеммы B 2 к клемме A 2	h 3 и h 4 второго выпрямителя
От 240° до 270°	От клеммы C 1 к клемме A 1	h 5 и h 4 первого выпрямителя
От 270° до 300°	От клеммы C 2 к клемме A 2	h 5 и h 4 второго выпрямителя
От 300° до 330°	От клеммы C 1 к клемме B 1	h 5 и h 6 первого выпрямителя
От 330° до 360°	От клеммы C 2 к клемме B 2	h 5 и h 6 второго выпрямителя

При расчётах учитывается, что в каждый момент времени через статическую нагрузку идёт только один ток (см. табл., столбец 2), а численное интегрирование для решения системы уравнений выполняется при замкнутой одной паре ключей (см. табл., столбец 3), остальные ключи разомкнуты.

Анализ кривых напряжения и тока генератора, полученные с использованием осциллографа Fluke 190 во время испытаний постов дистанционного контроля на подводной лодке «Кронштадт», и спектры напряжения и тока генератора, полученные с использованием программного

Математика

обеспечения прибора Fluke 190 методом дискретного быстрого преобразования Фурье, позволяет сделать вывод о большом вкладе 5-й, 7-й, 11-й, 13-й и 17-й гармоник в процесс формирования несинусоидальных тока и напряжения генератора, включённого на мощный выпрямитель. Это соответствует разработанной математической модели и вполне характерно для систем выпрямления, не имеющих схем пассивной компенсации высших гармоник.

Совокупность собранных диагностических параметров, результатов работы математических моделей оценивания технического состояния и прогнозирования составляет цифровой портрет дизель-генератора (его цифровой двойник на этапе эксплуатации).

Разработанная математическая модель дизель-генератора переменного тока со статической нагрузкой позволяет: на первом этапе (прямая задача диагностирования) – получить количественную оценку и провести категорирование технического состояния дизель-генератора на основе анализа отклонений фактических значений диагностических параметров от «эталонных» (приведенных к текущим параметрам режима и внешних условий), а на втором этапе (обратная задача диагностирования) – получить количественную оценку технического состояния дизель-генератора и его элементов с моделированием возможных неисправностей объекта диагностирования для последующего сравнения с накопленным массивом параметров технического состояния и определения возможных рисков отклонения от режима нормального функционирования.

На этапе диагностики технического состояния дизель-генератора собранные фактические и расчетные параметры технического состояния передаются в диагностическую систему для принятия управленческих решений. Для этого широко применяют беспроводные и цифровые технологии [22–26], а компенсация помех и искажений при регистрации и передаче характеристик состояния дизель-генераторов обеспечивается за счет применения методов теории оптимальных динамических измерений [27, 28].

Заключение

Разработанная математическая модель дизель-генератора переменного тока со статической нагрузкой является основой единой цифровой платформы функционирования переносных диагностических комплексов информационной поддержки жизненного цикла энергетических установок, эксплуатируемых на борту надводных кораблей и неатомных подводных лодок. Ее применение позволяет рационально планировать техническое обслуживание корабельных энергетических установок по фактическому состоянию. Кроме этого, предложенная математическая модель эффективно применяется в составе компьютерных учебных комплексов профессиональной подготовки экипажей надводных кораблей и неатомных подводных лодок.