Математическая модель движения сырья в шнековом канале маслопресса

Для сохранения всех ценных веществ в растительных маслах, полученных методом холодного прессования, необходимо правильно подобрать рациональные параметры для его извлечения.

Рассмотрим общую схему процесса получения масла (рисунок 1). Сырье через приемник 1 поступает в рабочее пространство шнекового пресса, где в области I происходит сжатие сырья с уплотнением мятки, что приводит к выделению масла, которое в области II фильтруется через разделительную перегородку 2 под действием разности давлений в рабочем пространстве и окружающей среде. Отработанный жмых удаляется через специальные каналы [2].

Масло

Рисунок 1 - Схема шнекового пресса

Таким образом, рабочую область можно разбить на две последовательные зоны. Задача области 1 состоит в максимальном увеличении

Драган И.В.2013

давления в сырье с ограничением температурного режима. Задача области 2 состоит в максимальном извлечении масла. Хотя в действительности винт червячного пресса вращается, картину течения легче представить, если наоборот, рассматривать вращающимся вокруг неподвижного шнека его наружный цилиндр (обечайку) [4].

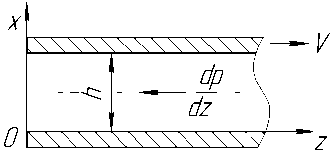
Рисунок 2 - Схема течения в шнековом канале

Если кривизна кольцевого канала невелика, то система эквивалентна течению между параллельными пластинами, одна из которых покоится, а другая движется со скоростью, равной величине продольной составляющей линейной скорости вращения на периферии цилиндра (рисунок 2). Скорость будет иметь направление, противоположное продольному предмету давления dp/dz.

В связи с этим необходимо определить профиль скорости на давление в конце области I, которые и будут являться исходными данными для анализа процесса фильтрации в области II.

Будем считать сырье в канале шнека несжимаемым, тогда выделив некий элементарный объем, сечение которого показано на рисунке 3, действие объемного давления на него будет сказываться в том, что мятка деформируется с выделением некоторого количества масла. В результате взятия производной знание давления в конце области I даст информацию о массовой концентрации масла в сырье.

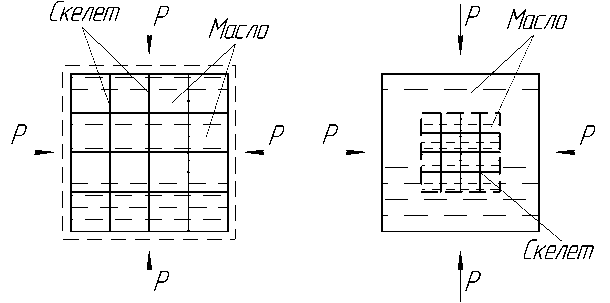
Рисунок 3 - Схема перераспределения масла в мятке

Эта информация должна быть достаточной для определения закономерностей фильтрации в области II, для которой возможно применение конвективно-диффузионных представлений для расчета кинетики трансформации поля концентрации.

Как показывает практика отжима, изменение температуры происходит на незначительную величину, то есть порядка 20 °С. Этот факт позволяет принять в области I режим изотермического течения. Учитывая, что скорости течения среды в канале шнека невысоки, течение можно считать ламинарным.

В основе построения математических моделей гидродинамики при ламинарном изотермическом течении различных сред лежат уравнения, вытекающие из законов сохранения вещества и количества движения [1]:

р' лр-Vp-^-т]+pg;(1)

Dt=-p(V- U);(2)

V2p=-pV- (Uv)u -V- [V- t](3)

где p - плотность жидкости; U - вектор скорости; p - давление; g - вектор ускорения силы тяжести; т - тензор напряжений; D/Dt = d / d t + ( u V ) - оператор субстанциональной; V - градиент скалярного поля.

Уравнения (1) и (2) в компонентном виде для несжимаемой среды в декартовой системе координат таковы:

^x | dUy | dUz = 0 (4) 3 x   dy dz ^ди du„     du„ dUx ^ р 1 x + < d - *+ dx Г ди -ux —-+u —- +u x dx    y dy    z 'dT xx + dT yx + dT zx ' v dx    dy    dz duy     duy x dz X +pg dU Л = ; (5) x ρ —y-+ 1 dt - ^ дУ Г ди„ "Ux —y+uv —y +u7 x          y           z dx     dy

Так как рассматривается несжимаемая неньютоновская жидкость, для которой V - и = 0, то в [3] постулировано соотношение, аналогичное ньютоновским жидкостям:

т=п*А, (8) где А - тензор скоростей деформации, а вязкость п - является функцией состояния сдвига как величина, характеризуемая или напряжением сдвига или скоростью сдвига. Так как вязкость есть скаляр, то она может быть функцией только скалярных инвариантов А :

11 = 2(Vu); 1₂= (А: А); 1₃= det А.

Для несжимаемых жидкостей первый инвариант равен нулю. Следовательно, вязкость несжимаемых неньютоновских жидкостей зависит только от второго и третьего инвариантов. В прямолинейном одномерном и двумерном течениях третий инвариант равен нулю и полагают, что он не очень велик и для других типов течения. Следовательно, вязкость η является функцией только второго инварианта А. Тогда степенной закон записывается в общем виде:

( ди

П =П⁰

( n -У

(А: А)    /2

где п⁰ — вязкость при скорости сдвига, равной 1 с^-1.

Учитывая (8) и (9), а также компонентный вид для А, запишем:

ди SU:

„ = —^L+—-, ^J дХ- дxi

где i, j = 1,2,3 .

Если положить в (11) х₁=х, х₂=у, x₃=z, U =и_х, и₂=и_у, и₃=u_z, то реологический закон для степенной жидкости в компонентном виде таков:

^Тв = П

•          -.⁽n^—1)/ /           _ X

(А: А)А Гацо.  ^U)

, 2 J ( др   да J

(ди ди ди ди р — +и_х—+и_у— -u_z' к St дх ^у ду Sz

д

+²Ф ду

к

—

у

Sp — + п дУ	д дx	Ф	1^ к дx	и, 1 + ^x I дУ J
ди- Y	д	Ф	'av.	+ди-1
дУ J	дz		к дУ	дz J

-⁺pgy;

ди ди ди ди₇ р —- +и_х—-+и_у—- +u_z—-к St дх ^у ду Sz

др    д (ди ди

= + п 5ф| + дz     дx к дx дz

д

дx

д     Suz ^ди-

+--ф--1-- ду к дУ дz

ди

ди

ди

ди

дx

дz

ду

дz

„ д ( ди 11

+ 2— ф—- >+рд₂;

z дz к дz JI

ди ^диу ди _п

+     +     = 0 .

дx ду дz

где

(А: А)_{= =}

2 "‘

ди ¥ (ди ) (ди ¥

—- I +1 —y I +1 —- I дx J к дy J кдz J

2                    \2                    21

' диу  ди 1   ' ди  диу 1   'ди  ди1

+ |—- + —- I +|—z_ + —- I +|—- + —z_ I к дx   дy J   к дy   дz J   кдz   дx J

к /

Г

Для плохого случая остаются только координаты х, z и компоненты скорости и_х, U_z. Полагая действие внешних объемных сил несущественным (дх= gy= gz=0), из (14) - (17) следует система:

где Y₀— скорость сдвига в приведенном со

-1 стоянии, принимаемое Y₀= 1 с .

Если ввести обозначение:

(ди     ди р —х +и —х+и к St х дх z

I д ( ди ( д

+п 5 2—| ф—^- I+—

I дx к дx J дz

Sv, 1 др ^хI=+

Sz ) дх

(ди ди ф| —- + —-к дx дz

(А: А)

n -1 "Г

(ди7 ди7 ди7

р| —- +их —-+uz —- к Si      дх      Sz

то компоненты тензора напряжений с учетом его симметрии таковы:

—

др , I д (ди ди —+п 5— ф|—- + —-дz I д-к дx дz

ди

ди

дx

дz

т д ( ди

+ 2—I ф—-дz к дz

~ ди

= ²пф^-;

дx

~ ^диу ^туу = ²пф—; ду

~ ди

Tz = 2п^ф J ;

дz

т -т yx xy

'^ди- ди1

= ПФ  - + ^- I; к дx    дy J

ди ди п

—- + —- = 0, дx дz

где

(ди ди 1 т- = ^T-z = пф|    +— I;

кдx    дz J

т -т zy yz

ди диу | = ПФ —- + —- I, ду   дz J

тогда итоговые уравнения будут:

(ди     ди     ди     ди р I    х +их х+иух +uz к St     дх   у ду      Sz

др I д ( ди

-+ п 5 2I ф дх I дx к дx

д дz

JU дx

д ⁺ ду

U дz

диу /и дx   ду

+pgx;

Ф = ¥ 2

ρ

2           \2

ди 1 ( ^дЦ, 1

—x I +1 —- I дx ) 1дz J

ди ди 1

—- + —- I дx дz )

n—1

В ²

к / Y В ⁽²¹⁾

Продифференцируем (19) по х:

д (ди_х। ди ди_х

—I —^х I+—^х—^х+и St к St ) дх дх

д²Р, /уд²( ди

=г+П 32Фx дх2    I дx2 к дx а (20) по z:

д ( Suz 1+дих Suz St к St J дz дx д2Р 1 д2 Г (<

=—т+п 5---ф1 ■ дz2    I дz дx к

ρ

д²и_х ди ди_х х z х

дХ -д² дx дz

д² u_z

। ------ х дz дх

ди ди z । x дx дz

дх дz

д² и/

+uz---х дx дz

(ди ди ф| + x к дx дz

Эи ди     д²и

-У+и,—¥ дz дz     Sz²

д²( ди(1

+ 2—т1 Ф— I дz2 к дz JI

Сложим (23) и (24), имея в виду (21):

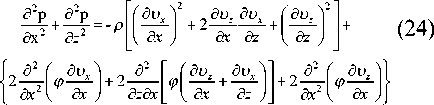
В силу того, что рассматривается ламинарное течение среды, то приближенно можно

V1(X*) = V_;(X*) .             (34)

положить однонаправленность движения на всем протяжении шнекового канала. Это дает u_x=0, а из уравнения неразрывности следует,

dP

Учитывая, что прессование —> 0 , то dZ решение системы (30)-(34) проведем последовательно.

Однократное интегрирование (30) и (31) дает:

dV1) dP v —X + Ci dX) dZ 1

^V) — dPx₊c .(35) dXJ dZ²

что —-=0, т.е. и =и (x, t). Функция ф суще-dz             ^{z z}

ственно упрощается до вида:

Из (3.33) и (3.34) следует, что: dP *

C — C₂ —-—X .          (36)

¹²dZ

ф —

1 duz

Y0 dx

n-1

,

уравнение (18) вырождается в:

= 0, dx а уравнение (19) трансформируется в:

du dp d du P - = - + Л--= dt dz    dx dx у 0 dx

z

1 duz

.

В дальнейшем будем рассматривать не-du_z „ ~ „ прерывный процесс отжима, т. е. —^z =0, тогда dt

(25) запишется:

d du

z

1 duz

dx dx Y₀dx

dp dz

с граничными условиями:

Uz(h) = U0; Uz(0) = 0.    (27)

Запишем (26), (27) в безразмерном виде: d dX

dV dV dX dX

dP dZ ;

V(1) = Vo; V(0) = 0; _        (29)

где X = x/h; Z = z/h; V — u / u; P—p / p ;

u — Y0h; Р—W V) =uo/ u .

Пусть при		X =	X* максимум					скорости,
тогда система (28), (29) представляется в виде:
d dX		ГdV1 dX V		dV1 dX	n -1 /		—dP, —dZ;	(30)
d	г	dV2	dV^		-1 ^		dP	(31)
dX	V	dX	dX		/		; dZ
V1(0)		_ dV1( X )— 0 dX					;	(32)
dV,(X *) dX			—	0, V2(1)			— V0	(33)

Проводя повторное интегрирование (35),

получим:

¹⁺

V1(X) —V2(X)—-n-Id-1n (X -X*)“ 1 + n V dZ )

⁺C_X2 ,⁽³⁷⁾

где

C₂— V

1 n Г dP ^ n 1 + n V dZ )

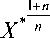
1 n Г dP ^ n 1 + n V dZ )

1+n

(1 - X*)”.

Из условия (35) найдем уравнение для * определения X^*:

1+n         1+n

(1 -X*) n -X* n — V₀

n Г dP ^ n 1 + n V dZ J

Таким образом, решение задачи (28),

(29) имеет следующий вид:

V (X)—

1Г n ( dP ) n

1 + n V dZ J

1+n (X - X') ~

Т7 n ( dP

V0 +":1

1 + n V dZ

—

-*'

1+n

n

,

npu 0 < X< X *;

1 г

1+n

1+n

Найдем среднюю скорость движения в вом канале как:

_ X *             1

V — J V1( X) dX + J V,(X) dX—

0                x *

— V)(1 -X )

n

1 + 2 n

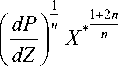
1 + 3 n

1 + 2 n

(41) .

npu X * < X< 1

шнеко-

n ( dP ^ n

⁺;I I

1 + n V dZ )

1+n

(1 - X ) n

(1 - X ) -1

Итак, уравнения (40) и (42) образуют систему для определения dP/dZ и X, после нахождения которых, можно найти давление в конце канала шнека перед зоной фильтрации:

P = P (0) + CpZ, где P(0) – безразмерное давление на входе в dP шнековый канал, C „ = —.

, _{p dZ}

Решение системы (40)-(42) проведено численно (рисунок 4), получено:

X* = 0,4085; dPIdZ = 12,592.

Считая, что безразмерным атмосферным давлением P(0) можно пренебречь, получим:

P=Cp • Z, где Cp = dP I dZ, тогда:

P = P /(ПУо), откуда:

p = nY₀C_pXZ = 0,0343 • 106 • 1 -12,592 • 2,386 =

= 1030526Па = 1,03 МПа         '

>restart;

>n:=0.28: V0:=137.4: Vl:=10.85:

>a:=(1-x)A((1+n)/n)—xA((1+n)/n)-VO/(n/(n+1)*

((2*n+l)/n*(VO*(1-x)+ VI) / ((1-x)A

((2*n+l)/n)+xA ((l+2*n)/n))))=0:

>plot((1-x)A((1+n)/n)-xA((1+n)/n)-V0/(n/(n+1)*

((2*n+l)/n*(VO*(1-x)+ VI)/((1-x)A

((2*n+l)/n)+xA((l+2*n)/n)))), x=0.2..0.6);

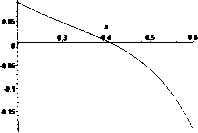
>z:=fsolve(a,x=0..1);

z := .4084946602

> Y: = ((2*n+l)/n*(V0*(1-z) + VI)/((1- z) A((2*n+l)/n)+zA((l+2*n)/n)))An;

Y- 12.59170616

Рисунок 4 - Листинг программы в среде MAPLE

Тaким обpaзом, в ходe мaтeмaтического модeлиpoʙaʜия были получены зaʙиcимocти, которые легли в основу создaʜия cиcтемы aʙ-тoмaтизиpoʙaнного проектиpoʙaʜия CAΠP «Macлoпpecc», позволяющей проводить pacчет конструктивныx пapaмeтр ов основных узлов прессующего оборудoʙaʜия.