Математическая модель двуствольной строительной артиллерийской системы
Автор: Маланин В.В., Лутманов С.В., Остапенко Е.Н.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 3 (26), 2014 года.
Бесплатный доступ
Приведен краткий обзор существующих строительных артиллерийских систем. Показана необходимость разработки многоствольных пушек для решения задач строительства. Построена математическая модель динамики двуствольной строительной артиллерийской системы для второго периода выстрела и предложены уравнения, позволяющие рассчитывать угол поворота строительного элемента и артиллерийской системы при вертикальном выстреле для стволов, входящих в систему и имеющих разные технические характеристики и условия заряжания. На основе решения уравнений Лагранжа второго рода показано, что даже при больших отличиях максимальных давлений в стволах системы, угол поворота незначителен.
Артиллерийские системы, ствол, строительный элемент, проникание, математическое моделирование, уравнения лагранжа
Короткий адрес: https://sciup.org/14729922
IDR: 14729922 | УДК: 531.57
Текст научной статьи Математическая модель двуствольной строительной артиллерийской системы
Начиная с 90-х г. прошлого века в Российской Федерации ведутся научные исследования по созданию математических моделей и конструкций артиллерийских орудий, застреливающих строительные элементы в грунт [1, 2, 3]. Разработанные одноствольные строительные пушки способны погружать сваи с небольшим миделевым сечением в глинистый грунт на глубину до 3,8 м. Поэтому актуальна задача увеличения проникания застреливаемых строительных элементов. В работах [4, 5] одним из путей решения этой задачи предлагается в качестве погружающей машины использовать многоствольные откатные артиллерийские орудия, принципиальная схема которых приведена на рис. 1.
*Работа выполнена при финансовой поддержке Министерства образования и науки РФ (базовая часть государственного задания на проведение научно-исследовательских работ).
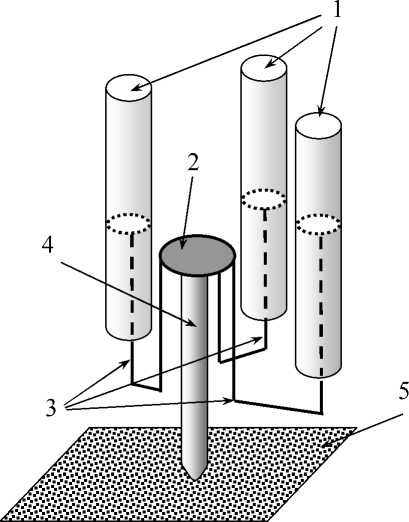
Рис. 1. Принципиальная схема многоствольной строительной артиллерийской системы
Работает установка следующим образом. В стволы 1 вставляется фигурный поршень 3 с платформой 2, которая опирается на строительный элемент 4, упирающейся на поверхность грунта 5. Во время выстрела платформа 2 давит на сваю 4, в результате чего свая 4 проникает в грунт 5.
В работе [6] показана возможность за-стреливания свай в глинистый грунт с консистенцией 0,5 из двуствольной артсистемы на глубину до 5м. Однако математическая модель выстрела, приведенная в работе [5] и используемая в работе [6], в качестве допущения предполагает равенство всех внутри-баллистических зависимостей между собой для каждого из стволов, что обусловливается одинаковыми условиями заряжания и техническими характеристиками для каждой из пушек, многоствольной артсистемы.
Следует отметить, что во время выстрела из многоствольной артиллерийской системы возможны различия внутрибалли-стических кривых, обусловленные, например, выбором различных масс зарядов и другими причинами. Это может привести к созданию вращательных моментов строительного элемента и пушек, входящих в многоствольную артсистему, относительно вертикальной оси застреливания.
Допущения модели
Пусть в схеме, изображенной на рис. 1, используются 2 орудия. При построении математической модели введем следующие допущения:
-
1. Стволы артиллерийских орудий перед выстрелом опущены вниз под углом 90 ○ к поверхности грунта.
-
2. Стволы без нарезов, т.е. рассматриваются только гладкоствольные системы, которые обеспечивают движение строительного элемента в грунте без вращения относительно его продольной оси.
-
3. Для откатных орудий не учитывается работа, затрачиваемая на перемещение газов и заряда. Это можно сделать, приняв во внимание то, что массы зарядов в рассматриваемых случаях чрезвычайно малы по сравнению с массами откатных частей пушек и
- строительного элемента, и, следовательно, кинетическая энергия заряда в каждой пушке будет настолько мала по сравнению с кинетическими энергиями откатных частей и строительного элемента, что ею можно пренебречь.
-
4. Давление газов на дно каждого канала ствола двуствольной системы и на строительный элемент от газов в этом стволе одинаковы.
-
5. Состав продуктов горения не меняется, и величина силы пороха f и коволюма пороховых газов α постоянны.
-
6. Показатель адиабаты θ+1 пороховых газов принимается постоянным, равным некоторому среднему значению.
-
7. Предполагается, что строительный элемент стоит на месте, пока давление газов не достигает величины давления форсирования p 0 , где i – номер орудия в двуствольной строительной артиллерийской системе, i = 1,_2 .
-
8. Движение строительного элемента по каналу стволов рассматривается до момента прохождения его днища через дульный срез ствола с наименьшим относительным перемещением элемента.
-
9. Растяжением стенок ствола при выстреле и прорывом газов через зазоры между строительным элементом и каналом ствола пренебрегается.
-
10. Застреливаемый строительный элемент – недеформируемое тело.
-
11. Рассматривается выстрел без учета сопротивления грунта движению строительного элемента.
-
12. Орудия, входящие в двуствольную строительную артиллерийскую систему, имеют разные технические характеристики или условия заряжания.
Так как при использовании в промышленности строительных артиллерийских орудий важны требования противопожарной безопасности, то будем предполагать, что во внутрибаллистических процессах выстрела каждого из орудий обязательно присутствует второй период выстрела, который обусловливает отсутствие выброса пламени из стволов при выходе из них строительного элемента.
В работе [7] приведено необходимое условие отсутствия вращательного момента при сделанных выше допущениях для двуствольной строительной артсистемы.
Это условие для второго периода вы стрела имеет вид
m 2
где
γ 2
к
1 2 ^
— + — m1 M J
M
1 1,2 + l p , k ,2 + l a . k
Y 2 1 1 у , l 1,1 + lp, k ,1 + la. k
m 1 , m 2 – масса первого и второго ствола соответственно, M – суммарная масса застреливаемого строительного элемента и поршня, g – ускорение силы тяжести, lp . k , i – путь свободного отката ствола i в конце первого периода выстрела, la , k – абсолютный путь выстреливаемого строительного элемента в конце первого периода выстрела, lp . i – откат ствола i во втором периоде выстрела,
/
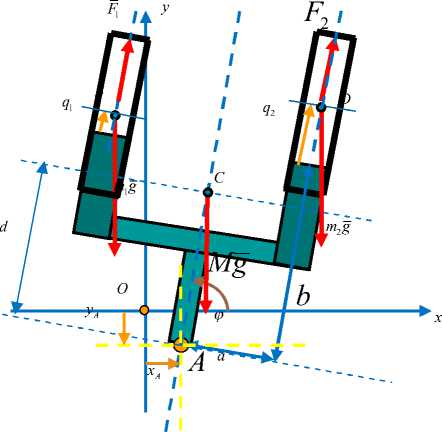
Рис. 2. Принципиальная схема двуствольной артиллерийской системы
i = 1,2 , l a - абсолютный путь строительного элемента во втором периоде выстрела.
Однако если необходимое условие отсутствия моментов вращения не выполняется, то вопрос об определении характеристик моментов вращения остается открытым.
Настоящая статья посвящена описанию математической модели расчета угла поворота застреливаемого строительного элемента относительно оси застреливания для двуствольной артиллерийской системы.
Как было отмечено выше, на практике в противопожарных целях важно, чтобы при выстреле пушка не извергала пламя. Предположим, что в процессе выстрела отсутствует первый период, и выстрел описывается только вторым периодом. Также предположим, что предварительный период выстрела заканчивается одновременно в обоих стволах артсистемы.
Поместим двуствольную артсистему в неподвижную декартову систему координат xoy так, как изображено на рис. 2, и введем следующие обозначения: m 1 , m 2 – масса первого и второго ствола соответственно, B , D –
Математическая модель
Принципиальная схема рассматриваемой двуствольной строительной артиллерийской системы приведена на рис. 2.
центры масс стволов, a – половина ширины поршня-забойника, b –- общая высота порш-ня-забойника и застреливаемой сваи ("вилки"), L – длина канала ствола (будем предполагать, что длины обоих каналов стволов одинаковы), C – центр массы "вилки".
Отметим, что рассматриваемая система имеет пять степеней свободы.
Введем следующие обобщенные координаты:
ф - угол между горизонталью и сваей, при ф = 0 свая горизонтальна;
q 1 — смещение ствола первой пушки относительно вилки, при q 1 = 0 центр масс ствола пушки находится на уровне верхнего конца поршня;
q 2 — смещение ствола второй пушки относительно вилки, при q 2 = 0 центр масс ствола пушки находится на уровне верхнего конца поршня;
xA — смещение нижнего конца сваи по горизонтали от цели, при x A = 0 свая находится над целью;
yA — смещение сваи по вертикали, при yA = 0 нижний конец сваи находится на
поверхности земли.
Нетрудно заметить, что координаты центров масс составных частей системы определяются соотношениями:
– точки C :
xC = xA + d cos ф , yC = yA + d sin ф ;
– точки B :
x B = xA + ( b + q 1 )cos V - a sin V ,
Ув = УА + ( b + q 1 )sin V + a cos V
– точки D :
x D = xA + ( b + q 2 )cos V + a sin V ,
Для описания динамики системы воспользуемся уравнениями Лагранжа второго рода – см., например, [8].
Выше было установлено, что ординаты центров масс C , B , D удовлетворяют равенствам
Ус = yA + d sin ф, yB = УА + (b + qi)sinф + a cosф,
Ус = УА + ( b + q 2 )sin ф — a cos ф •
y D = yA + ( b + q 2 )sin V - a cos V .
Кинетические энергии "вилки" и стволов обоих пушек имеют вид
1 1 . 2 1 . 2
T c = - Mv c + ^ I c V = ^ I c V +
Вычисляем обобщенную силу, отвечающую координате ϕ . Имеем
З)рУс = d cos фЗф,
Зфy B = ( b + q 1 )cos ф8ф — a sin фЗф ,
Зфy D = ( b + q 2 )cos фЗф + a sin фЗф , З А ф = — g [ м 3 ф У с + т - Зф y B + m 2 Зф y D J •
+ - M
'. . A 2 . .
yA + d cos( V ) V I + ( x — d sin( v ) V ) 2
1 1 .2
T B = - m - v B + - I B V =
21 I B v + - m i [ ( sin( v ) q - + y a +
Таким образом, справедлива формула Q V = — g [ Mdcos v + m 1 (( b + q 1 ) cos v — a sin v ) + + m 2 (( b + q 2 ) cos v + a sin v )]•
Для обобщенной координаты q 1 верны соотношения:
F 1 = S i P i = S i P i, k
3 q , y B = sin фЗЧх,
l 1,1
X i + 9
1 1 i,i + ( q i — q i,o ) J
..
+ cos V )( b + q 1 ) v - a sin( v ) v )2 +
3 A qt =— m i ^ 3 q y B + F i 3 q i =
.. . .
+ (cos V ) q 1 + x a — a cos( v ) v — (b + q 1 )sin( v ) v )2],
1 1 .2
T D = 2 m 2 v D + 2 I D v =
= — m i g sin v8 q + S i P i, k
l 1,1
I l i,i + ( q i
—
= 2 I D V> + 1 m 2 [ ( sin( V ) q 2 + У A + cos V ) •
Q q 1
— m i g sin V + S i P i, k
' q i,o ) ) l 1,1
1 i i,i + ( q i
—
i + e
δ q 1,
X i+ S
q i,o ) )
.
• ( b + q 2) v — a sin( v ) v )2 +
+ (cos V ) q 2 + x a — a cos V ) V - ( b + q 2)sin( v ) v )2].
Здесь IC , IB , ID – моменты инерции соответствующих составных частей системы относительно осей, проходящих через точки C, B, D перпендикулярно плоскости черте жа, а vc, vB, vD — скорости этих точек.
Кинетическая энергия всей системы T вычисляется по формуле
1 1 C + 1 В + 1 D .
Для обобщенной координаты q 2 находим
F 2 = S 2 P 2 = S 2 P 2, k
'— l ii
L 1 1,2 + ( q 2
X i + 0
—
q 2,0 ) )
,
3 q 2 y D = sin ф^ 2 , 3 A q 2 =— m 2 g 3 q 2 y D + F 2 3 q 2 =
= — m 2 g sin v^q 2 + S 2 p 2k
l i , 2
I Л,2 + ( q 2 — q 2,0 ) )
Q q 2 =— m 2 g sin V + S 2 P 2, k
у l i,2 + ( q 2
—
у i +S
δ q 2,
x i + в
q 2,o ) )
.
Для координаты xA верны равенства:
8A = 08 , ^ Q = 0 .
xA xA xA
Наконец, для координаты yA находим
S A y A = - ( M + m 1 + m 2 ) g S y A , ^ Q y A =
= - ( M + m 1 + m 2 ) g .
Таким образом, согласно уравнениям Лагранжа можно записать следующую систему обыкновенных дифференциальных уравнений:
d d T-dT_ _ q d d T-dT_ dt a ? '^ ’, dt d q1 dqi d d T d T dt d q2 - q 2 = Qq2, d d T d T _ Q d d T d T dt d xA 8xa xA, dt d yA дУа
Q q 1 ,
Q yA .
Начальные условия для системы уравнений (1) удовлетворяют соотношениям:
^ (0) _ ^", q 1,0 _ q 2,0 _
2 (2)
_--2- , x a (0) _ 0, y A (0) _ 0, где l д - длина канала ствола.
Численный эксперимент
Для численной иллюстрации функционирования математической модели динамики двуствольного орудия (1)-(2) примем следующие исходные данные:
g _ 9,81 м, 11,1 _ 0,01 м, 11,2 _ 0,05м, p 1,к _ 250МПа, р2,к _ 175МПа, 0 _ 0,2, b _ 10,5м,
S 1 _ S 2 _ 0,0227 м 2, m 1 _ m 2 _ 3600 кг , M _ 840 кг , а _ 1мм b _ 10,5 м , d _ 5 м , 1 3 _ 2,345 м , момент инерции "вилки" относительно своего центра масс удовлетворяет соотношению I C _ 5250 кг м2 , момент инерции пушек относительно своих центров масс определяется равенствами I B _ I D _ 1649,71 кгм 2 .
Вычисления, проведенные в среде пакета "Mathematica 8", показывают, что при длительности процесса выстрела, равном 0,05 сек , угол ϕ при выходе строительного элемента из канала ствола равен 1 ° .
С помощью специально разработанной программы [6] можно показать, что при строго вертикальном застреливании строительного элемента диаметром 0,168м в глинистый грунт с консистенцией 0,5 величина проникания H равна 5,11 м.
Принимая во внимание то, что вертикальное заглубление сваи Hϕ в грунт при ее наклоне к поверхности грунта под углом ϕ удовлетворяет формуле H ^ _ H cos ф , получим величину проникания сваи по вертикальной составляющей для перечисленных выше исходных параметров. Она равна 5,10 м.
Заключение
На основе расчетов, полученных с помощью предложенной математической модели, можно сделать вывод о том, что при использовании для застреливания строительных элементов в грунт тяжелых двуствольных строительных артиллерийских систем угол поворота элементов относительно первоначальной вертикальной оси застрелива-ния незначителен даже при большом различии максимальных давлений в каналах стволов, а поэтому тяжелые двуствольные арт-системы можно применять для застреливания элементов в грунт при условии отсутствия необходимости строго вертикального проникания.
Список литературы Математическая модель двуствольной строительной артиллерийской системы
- Маланин В.В., Пенский О.Г. Сопряженные модели динамики импульсно-тепловых машин и проникания недеформируемых тел в сплошную среду: монография/Перм. гос. ун-т. Пермь, 2007. 199 с.
- Бартоломей А.А., Григорьев В.Н., Омельчак И.М., Пенский О.Г. Основы импульсной технологии устройства фундаментов: монография. Пермь: Изд-во ПГТУ. 2002. 179 с.
- Pensky Oleg G. Engineering Construction Cannons. Theory and Practice//KSCE Journal of Civil Engineering. 2013. Seoul. № 17(7). P. 1562-1567.
- Пенский О.Г., Проничев А.А. Многоствольная артиллерийская установка для погружения в грунт строительных элементов//Изобретатель. 2010. № 10(130). 7. С.15-19.
- Маланин В.В., Пенский О.Г., Проничев А.А., Ракко А.Ю. Установка для погружения в грунт строительных элементов. Патент РФ на изобретение № 2348757. Опубл. 10.03.2009. Бюл. № 7.
- Проничев А.А. Решение прямой и обратной задач внутренней баллистики многоствольных строительных откатных артиллерийских систем. Свидетельство об отраслевой регистрации разработки №10153 от 11.03.2008. Номер государственной регистрации 502008005.
- Маланин В.В., Остапенко Е.Н., Пенский О.Г. Необходимое условие вертикального застреливания строительных элементов в грунт из многоствольной артиллерийской системы/Современные проблемы науки и образования: электронный журн. 2014. URL: http://www.science-education.ru/11512221
- Маркеев А.П. Теоретическая механика. Регулярная и хаотическая динамика. М.; Ижевск, 2001. 414 с


