Математическая модель электродвигателя постоянного тока рулевой машины жидкостного ракетного двигателя

Проведение системного анализа электромеханической следящей системы управления вектором тяги жидкостного ракетного двигателя пилотируемого транспортного корабля предполагает выполнение её декомпозиции на законченные функциональные элементы и идентификацию их параметров. В структуре электромеханической рулевой машины может быть выделен источник механической мощности — приводной магнитоэлектрический двигатель (МЭД) (электродвигатель постоянного тока с возбуждением от постоянных магнитов). В соответствии с теорией электрических машин [1], связь между электродвижущей силой якоря E _я и угловой скоростью вращения вала МЭД ω, а также между вращающим моментом M и током якоря I , определяется единым электромагнитным коэффициентом

k

э

pN

= Φ, 2π a где N — полное число проводников обмотки якоря; p — число пар полюсов машины; а — число пар ветвей; Ф — магнитный поток полюсов.

Тогда E _я = k _эм ω; M = k _эм I , а динамический процесс работы МЭД в общем случае, в соответствии с теорией электрических машин, описывается следующей системой дифференциальных уравнений [1]:

L-T- + RI + к ю = U; а эм dω k I – M = J , эм c dt где L — индуктивность обмоток якоря; R — активное сопротивление якоря; U — напряжение питания, подаваемое на МЭД; J — момент инерции вращающихся частей, приведённый к валу двигателя; Мс — статический момент или момент сопротивления, который в общем случае равен сумме нагрузочного момента M и момента сухого трения МЭД Mст (Мс = M + Mст); ω — угловая скорость вращения вала МЭД.

В некоторых публикациях [2] для моделирования МЭД используются два разных коэффициента, Cе и Cм, однако использование такой модели предполагает знание значения магнитного потока полюсов Ф, который не входит в перечень паспортных данных МЭД.

В других публикациях [3] пользуются разными обозначениями коэффициента электромагнитной скоростной связи МЭД K _э и коэффициента моментной характеристики МЭД K _м , однако в системе единиц измерений СИ эти коэффициенты считают равными.

Как показывает опыт работ по моделированию большого количества рулевых машин [4–6], параметры реальных МЭД часто отличаются от номинальных заявляемых данных. Повысить точность математической модели МЭД возможно путём применения вместо одного единого электромагнитного коэффициента двух различных коэффициентов математической модели: электромагнитной скоростной связи МЭД K _э и моментной характеристики МЭД K _м . Скорее всего, эти коэффициенты будут иметь близкие, но не равные значения. В этом случае математическую модель МЭД можно представить следующим образом:

dI

L d- + ri + К э й = U ;          (1)

d ω

K м I – M – M cт = J_dt .         (2)

Методы идентификации параметров L и J математической модели МЭД, влияющих только на динамические процессы работы МЭД, хорошо отработаны и общеизвестны [7], поэтому настоящая работа посвящена разработке метода идентификации параметров, влияющих на статические режимы работы МЭД.

метод идентификации параметров уточнённой математической модели электродвигателя постоянного тока с возбуждением от постоянных магнитов

Метод идентификации параметров K _э , K _м и других удобно продемонстрировать на примере идентификации этих параметров МЭД марки ДП32-25-4-27-IM3681-P11-Д31 [8] с возбуждением от постоянных магнитов.

Статические характеристики электродвигателей определяются с помощью экспериментальной установки, включающей в себя специальный нагрузочный стенд, позволяющий создавать на валу электродвигателя постоянные моменты сопротивления вращению. Схема такой экспериментальной установки представлена на рис. 1.

Температура и напряжение питания электродвигателя при проведении экспериментов считались постоянными ( T = const; U = const).

В процессе экспериментов определялись зависимости скорости вращения выходного вала и тока, потребляемого электродвигателем, от момента сопротивления на валу в виде следующих комплексов пар данных:

ω _i = ω( M_i ); (3)

I_i = I ( M_i ). (4 )

Экспериментальные данные МЭД ДП32-25-4-27-IM3681-P11-Д31, полученные с помощью экспериментальной установки, после статистической обработки, приведены в таблице.

экспериментальные данные статических характеристик мэд

М , Н·м	ω , рад/с	I , А
0	437	0,13
0,01	433	0,32
0,01	430	0,50
0,03	427	0,72
0,04	425	0,87
0,05	421	1,06
0,06	419	1,25

Статические характеристики МЭД при Ф = const, согласно теории электрических машин, представляют собой прямые линии, наклоненные к оси абсцисс, описываемые следующими соотношениями:

ω = ω ₀ – K _ω M ;              (5)

I = I ₀ + K_IM ,                 (6)

где ω ₀ — максимальная угловая скорость при отсутствии момента сопротивления, создаваемого на валу МЭД; K _ω — коэффициент изменения угловой скорости под воздействием момента, создаваемого на валу МЭД; I ₀ — минимальный потребляемый ток при отсутствии момента, создаваемого на валу МЭД; K_I — коэффициент приращения потребляемого тока под воздействием момента, создаваемого на валу МЭД.

Для определения входящих в выражения (5) и (6) параметров ω ₀ , K _ω , I ₀ , K_I воспользуемся методом наименьших квадратов [9].

Составляем минимизируемые функционалы:

n

F1 = ∑ г - 1

ω _i – ω ₀ + K _ω M_i = min;

F 2 = ∑ I i – I 0 – K I M i

г - 1

= min,

где n — количество экспериментальных пар данных зависимостей (3) и (4).

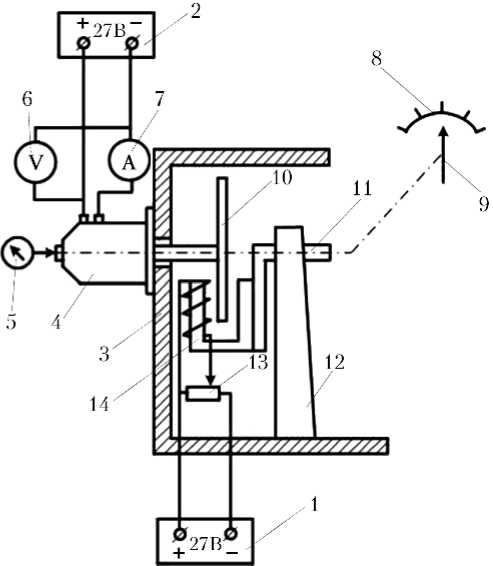
Рис. 1. Схема экспериментальной установки для снятия статических характеристик электродвигателей: 1, 2 — стабилизированные источники напряжения; 3 — нагрузочный стенд; 4 — МЭД; 5 — бесконтактный тахометр; 6 — вольтметр; 7 — амперметр; 8 — шкала; 9 — стрелка; 10 — медный диск; 11 — вал; 12 — стойка; 13 — регулировочный потенциометр; 14 — поворотный электромагнит

Необходимым условием существования минимумов выражений (7) и (8) является равенство нулю частных производных от F ₁ и F ₂ по каждому из входящих в эти выражения идентифицируемых параметров, т. е.

∂ F 1 ₌ ∂ω ₀

n

∑ ω i – ω 0 + K ω M i (–1) = 0;

г - 1

∂ F ₁

∂ K ω

n

= ∑ ω _i – ω ₀ + K _ω M_i M_i = 0.

г - 1

∂ F ₂ ∂ I 0

∂ F ₂

∂ K_I ⁼

n

∑ I i – I 0

г = 1

n ∑ г - 1

– K_IM_i (–1) = 0;

I_i – I ₀ – K_IM_i M_i = 0.

Таким образом, для идентификации всех искомых параметров необходимо решить следующие системы уравнений:

nn

-Уо. + n о_п - К У У, = 0;

^^ г       0 о ^^ г ¹

г - 1                                   г - 1

n  nn

У о У. - ю_п У У, - К  У ² = 0;

^^ г г 0 ^^ г о ^^ г ¹

г = 1                          г = 1                      г = 1

nn

– ∑ I i + nI 0 + K I ∑ M i = 0;

i = 1                            i = 1

nnn

IM – I M – K M ² = 0. ii 0 i I i i = 1                    i = 1                  i = 1

Решение полученных систем уравнений возможно методом Зейделя [10], но удобнее для определения параметров ω ₀ , K _ω , I ₀ , K _I воспользоваться программой 5.18 «линейная регрессия» из работы [11]. В результате вычислений получаем:

ω ₀ = 436,32 рад/с;

K _ω = 296,428 рад/с·Н·м;

I ₀ = 0,1346 А;

K _I = 18,61 А/Н·м.

С другой стороны, математическая модель статического режима работы электродвигателя постоянного тока, получаемая, если приравнять нулю производные в уравнениях (1) и (2), и соответствующая режиму снятия характеристик исследуемого электродвигателя, описывается следующими уравнениями:

RI + Kэω = U.(9)

M + Mст = KмI.(10)

Преобразуем уравнения (9) и (10) к виду

U МR R ю = ^ -1<1г-КПГм• э эм эм

М 1

I = _K ^ст + _K M ^. мм

Тогда, сравнивая выражения (5) и (11), (4) и (12), параметры ω ₀ , K _ω , I ₀ , K_I можно определить следующим образом:

U	М ст R	(13)
ω 0 = K – э	K э K м ;
R		(14)
K ω = K э K м	;
М ст I 0 = K м ;		(15)
K I = K 1 .		(16)

Из полученных уравнений (13)–(16) после преобразований получаем выражения для идентифицируемых параметров:

Kм = 1 ;(17)

I

Mст = I0Kм;(18)

Kэ = ω + K М ;(19)

0 ω ст

R = KωKэKм.(20)

Проводя вычисления по формулам (17)–(20), осуществляем идентификацию параметров K _э , K _м , R и М _ст :

электродвигателей устанавливают в якорную цепь дополнительное сопротивление, создавая тем самым у МЭД искусственную статическую характеристику. При этом параметры статического режима работы МЭД с такой искусственной характеристикой отличаются от параметров статического режима работы МЭД с естественной характеристикой. Поэтому всегда необходимо проверять применяемый МЭД на наличие искусственной статической характеристики. Это легко сделать, проведя непосредственное измерение сопротивления якорной цепи МЭД. Если оно отличается от полученного в результате идентификации, то МЭД имеет искусственную статическую характеристику.

Для идентификации параметров статического режима работы МЭД, имеющего искусственную статическую характеристику, необходимо выполнение тех же действий, что и при идентификации параметров статического режима работы МЭД, имеющего естественную статическую характеристику. Затем выполняются следующие действия:

• •    идентифицируют параметры K _м и М _ст по выражениям (17) и (18);

• •    осуществляют непосредственное измерение активного сопротивления якорной цепи МЭД при нескольких положениях выходного вала

электродвигателя;

K _э = 0,0616 В⋅с/рад;

K _м = 0,0537 Н·м/А;

R = 0,98 Ом;

М _ст = 0,00723 Н·м.

Параметры K _э и K _м , как это и ожидалось, имеют близкие, но не равные значения. Если бы в результате идентификации эти параметры оказались практически равными, то это подтвердило бы правильность теории электрических машин, но этого не произошло.

Однако следует отметить, что разработанный метод пригоден только для идентификации параметров статического режима работы МЭД, имеющего естественную статическую характеристику. Очень часто для снижения пускового тока МЭД производители

• •    определяют максимальное значе-

  ние активного

  
  

  цепи R

  max

  
  

  ;

  
  

  • вводят

  
  

  в

  
  

сопротивления якорной якорную цепь МЭД дополнительное сопротивление, составляющее 1% от Rmax;

• •    подают на МЭД номинальное напряжение питания U и осуществляют осциллографирование пускового тока I _п по сигналу с дополнительного сопро-

• тивления;

• •    определяют по осциллограмме пусковой ток I _п ;

• •    идентифицируют параметры R и K _э по выражениям

^R = 4 ;                (21)

п

U – IR

K э =       ⁰ .                 (22)

ω ₀

Последнее уравнение получено подстановкой М _ст , получаемого из выражения (18), в выражение (13) и разрешением его относительно K _э .

Для МЭД ДП32-25-4-27-IM3681-P11-Д31 оказалось, что измеренное активное сопротивление его якорной цепи примерно в два раза выше полученного при идентификации по выражению (20). Следовательно, этот МЭД имеет искусственную статическую характеристику. В результате осциллографи-рования пускового тока было определено его значение I _п = 13,17 А. В результате вычисления по выражению (21) было определено значение активного сопротивления якорной цепи МЭД ДП32-25-4-27-IM3681-P11-Д31 R = 2,05 Ом.

Окончательное значение коэффициента электромагнитной скоростной связи было получено вычислением по выражению (22) K _э = 0,061175 В·с/рад.

Графики зависимости скорости вращения вала электродвигателя и тока, потребляемого МЭД ДП32-25-4-27-IM3681-P11-Д31, от момента, создаваемого на его валу, полученные в результате моделирования статического режима работы МЭД с параметрами, определёнными в процессе идентификации, а также данные экспериментов приведены на рис. 2.

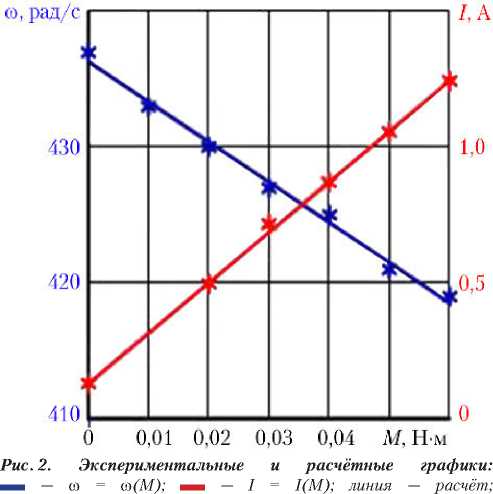
* — эксперимент

Как видно из рис. 2, расчётные графики и данные экспериментов практически совпадают, что указывает на корректность уточнённой математической модели МЭД, а также на высокую точность и эффективность разработанного метода идентификации её параметров.

заключение

В итоге описанных в настоящей статье разработок и исследований получены следующие основные результаты:

• •    разработана математическая модель МЭД, где вместо единого электромагнитного коэффициента применены два различных коэффициента математической модели: электромагнитной скоростной связи K _э и моментной характеристики K _м ;

• •    разработаны методы идентификации параметров уточнённой математической модели МЭД, имеющих естественную и искусственную характеристики.

Вывод по результатам проведённых исследований: для повышения точности моделирования МЭД вместо единого электромагнитного коэффициента следует применять два различных коэффициента математической модели, а именно — коэффициент электромагнитной скоростной связи и коэффициент моментной характеристики.