Математическая модель оценки стоимости программы путем сравнения с аналогами

Построение экономики развития, выход ее на технологические рубежи, практическая реализация концепции экономической модернизации предполагают разработку методологических подходов и развитие теоретических положений института собственности. Важнейшей задачей государства в посткризисный период является совершенствование институтов инноваций. Измерение истинной стоимости активов методом математического моделирования позволит снизить его субъективность (минимизировать человеческий фактор) и использовать предложенный подход при формировании информационной базы кадастровых расчетов оценки.

Анализ исследований отечественных авторов по оценке объектов интеллектуальной собственности [1–11 и др.] указал на отсутствие в них адекватных рыночным условиям процедур определения стоимости программ для ЭВМ и баз данных, актуальность и необходимость проведения которых возрастает. Отметим, что лишь в [12] подробно рассмотрена оценка программ для ЭВМ и баз данных и приведены учебные примеры расчета их стоимости, но математическая модель оценки не построена.

Необходимость разработки указанной модели связана с тем, что при продаже или лицензировании программ для ЭВМ и баз данных требуется определить их рыночную стоимость, а количество зарегистрированных в России договоров о передаче исключительного права на эти объекты росло даже в кризисные 2008–2009 гг. [13]. Кроме того, регистрация при бюджетных вузах и организациях академий наук хозяйствующих обществ, внедряющих результаты интеллектуальной деятельности, требует оценки вклада в уставной капитал объектов интеллектуальной собственности (включая программы для ЭВМ и базы данных) [14].

Целью работы является построение математической модели оценки стоимости программы путем сравнения ее характеристик с характеристиками и ценами аналогов.

Постановка задачи

Пусть имеется объект оценки A ₀ (программа для ЭВМ или база данных) и m его аналогов A 1 - A m . При этом объект и аналоги имеют n характеристик X 1 - X n . Характеристики со своими весами ® 1 - to n определяют известные стоимости аналогов C 1 - C m и неизвестную стоимость C 0 объекта оценки. Известны также численные значения всех характеристик для аналогов ( x_ij ) и объекта оценки ( x i 0 ) (табл. 1). Требуется найти стоимость объекта оценки C ₀ .

Значения некоторых характеристик у ряда аналогов и объекта оценки могут быть равны нулю, если эти функции у них отсутствуют.

С ростом значения одних характеристик стоимость программы возрастает, а с ростом значения других - убывает. Назовем первые характе-

Таблица 1

Характеристики и их значения для аналога и объекта оценки

Характеристики (функции, возможности) программы Вес Величины характеристик Аналоги Объект оценки A1 A2 Aj Am A0 X1 to1 x 11 x12 x 1 j x1m x10 X2 to 2 x21 x22 x2j x2m x20 Xi toi xi1 xi2 xij xim xi0 Xn ton xn1 xn2 xnj X nm xn0 Стоимость C1 C2 Cj с m с 0 - ? ристики позитивными, а вторые - негативными. Предлагаем преобразовать все негативные характеристики Xi и их величины xij в позитивные характеристики Yi и их величины у у как Y = 1, Xi и У у = 1 xij .

Возможно, что ряд характеристик имеет по l дублирующих характеристик. Из расчетов необходимо исключить все эти характеристики кроме одной. Иначе, будем присваивать веса всем дублирующимся характеристикам, тем самым повысим в l раз вес одной характеристики (выраженной разным образом), а веса других (недублирующихся) характеристик будут уменьшены. Отметим, что в [12], к сожалению, есть ошибка, связанная с присутствием в расчетах двух дублирующихся характеристик - «пропускной способности канала» и «времени переходного процесса», так как вторая является ограничивающей для первой [15].

Расчет стоимости программы для ЭВМ по цене программ аналогов

Пусть теперь все характеристики X1 – Xn позитивные и не дублируют друг друга. Баллы качества характеристик Xi аналогов Aj и объекта оценки будут определяться как qij = xij ^i I max ( xi0, x1, xi2 • " xim ) , где в числителе - сумма произведений значений характеристик программы на веса этих характеристик, а в знаменателе - максимальное значение характеристики среди аналогов и объекта оценки (табл. 2).

К примеру, балл качества второй характеристики ( i = 2) у первого аналога ( j = 1) будет

nn q 2 = 2 qi2 = 2

i = 1           i = 1

_____________xi2 toi_____________ max ( xi0, xi1, xi2 • xim ) .

Стоимость одного балла качества Q_j , опреде-

ленная по аналогу A_j составит

Q j ⁼ , = - q j ₂

i = 1

x ij ^to i

,

max ( x i0 , x i1 , x i2 • x im )

а усредненная стоимость одного балла качества по всем аналогам

A

m

1 ^m

m

n

V i = 1

C

x ij ^to i

max ( x i 0 , x i1 , x i2 • x im )

.

Стоимость одного балла качества есть, по существу, отношение цена/качество. Подобрать аналоги так, чтобы отношение цена/качество у них было близко к объекту оценки можно по близости набора их функций и значений характеристик. Если это отношение для ряда аналогов заметно отличается от остальных аналогов, это означает, что данные программы принадлежат другим классам качества. Эти программы нужно исключить из расчетов.

Тогда стоимость объекта оценки, набравшего суммарный балл качества

n q о =2

i = 1

x i0 ^to i

max ( x i0 , x i1 , x i2 • x im )

будет

A

x 21 to 2

q 21 =      7                       7 .

max ( x 20 , x 21 , x 22 x 2 m )

Тогда суммарный балл качества, набранный аналогом или объектом оценки A_j :

0 = ^Qq 0

m

=12

m j = 1

n

V i = 1

C

x ij ^to i

max ( x i 0 , x i1 , x i2 ••• x im )

nn qy = 2 qy = 2

i = 1          i = 1

______________xij toi_______________ max ( xi0, xi1, xi2 • xim ) .

n

- 2

i = 1

_____________ x i 0 ^to i ______________ max ( x i0 , x i1 , x i2 ••• x im )

Так, суммарный балл качества для аналога A ₂ ( j = 2) будет

или в других обозначениях

Таблица 2

Баллы качества аналогов и объекта оценки

Характеристики	Баллы качества
	Аналоги				Объект оценки
	A 1	A 2	A j	A m	A 0
X 1	q 11	q 12	q 1 j	q 1 m	q 10
X 2	q 21	q 22	q 2 j	q 2 m	q 20
Xi	q i 1	q i 2	q ij	qim	q i 0
X n	q n 1	q n 2	q nj	q nm	q n 0
Суммарный балл качества	q 1	q 2	q j	q m	q 0

Любимов С.В., Тарасов О.А.

m

C 0 =¹ Z m j = i

C j

A Mmax i у

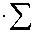
xi0 to maxi

где max i = max ( x i ₀, x i 1 , x i 2 . . x_im ) - максималь-

ное значение характеристики среди аналогов и объекта оценки в строке табл. 1.

Данную формулу можно использовать для оценки любых объектов, если стоимость объекта и

где Д q , и Д q ₀ - поправки к суммарным баллам качества аналогов и объектов оценки, соответственно, внесенные в уравнение (1), а Q _д и q _{0 Д} - усредненная стоимость одного балла качества по всем аналогам после внесения поправок и стоимость объекта оценки после внесения поправок.

Из (2) видно, что внесение поправок Д q , к

суммарным баллам качества аналогов q _j вызыва-

ет изменение усредненной стоимости балла каче-

его аналогов растет прямо пропорционально зна-

чениям их характеристик.

Веса характеристик

Согласно (1) увеличение абсолютного значения весов для аналогов и объекта оценки в одно и

то же число раз N не сказывается на стоимости

ства по всем аналогам, даже если вносится только одна поправка. Внесение же поправки к суммарному баллу качества объекта оценки изменяет только его суммарный балл качества. Однако изменение суммарного балла качества программы (все равно - аналога или объекта оценки) эквива-

объекта оценки, так как оно взаимно сокращается.

лентно тому, что при тех же характеристиках про-

Действительно

граммы, веса ее характеристик изменились, по

сравнению с весами тех же самых характеристик у

m

1Z

m , = 1

c j z x i, to N

A i = 1 ^max i

11 ^m mN ^Z

m

=1 z m ,=

_x ■ ^Xi0 to ^N i = 1 ^max i

А

cj

Z x ij ® i a Mmax i у

■ N Z - i ⁰— i i =1 max i

C

n

Z x ij ® i

A i = 1 max i у

max _i

Таким образом, сумма весов характеристик не обязательно должна быть равна 100 % или 1 (это просто удобнее), а может быть любым положитель-

ным числом.

Поправки к баллам качества

В журнале Computer Bild [16] часто вносят поправку к баллу качества программы (как аналога, так и объекта оценки) после того, как баллы

определены на основании значения характеристик

и весов характеристик в стоимости программы. Докажем состоятельность подобной поправки.

Стоимость объекта оценки C _д , определенная

при внесении поправок, в общем случае будет

иметь вид

или

( m

C д=¹ Z

m

C j

( q , ^+д J

)

■ ■ ( q 0 + ^д q 0 ) = Q д - q 0 д ,    ⁽²⁾

других программ. Разумеется, делать такие поправки нельзя. Действительно, балл качества указанной программы будет

q , ^+д q , =1 Z

A i = 1

x ij ^ i max _i

л      Z x ij ® iД

^+д q , = z---- i - 1 max i

где to _{i Д} - веса характеристики у j -й программы

после внесения поправки к суммарному баллу качества этой программы

С другой стороны, поправку к баллу качества

программы можно рассматривать как поправку за характеристику (модуль, возможность), которой нет у других аналогов или объекта оценки. В этом случае поправки не вносят изменений в веса ос-

тальных характеристик, т. е. такие поправки делать можно. Действительно, балл качества такой

программы будет

I n q,+д q, =1Z

A i = 1

x jj ^to i max _i

n + k

+ д q, = Z i=1

x ij ^to i max _i

где k - число дополнительных характеристик по всем аналогам и объекту оценки, по которым вносятся поправки к баллам качества этих программ. Если для данной программы при заданном номере характеристики в диапазоне [ n + 1, n + k ] поправка

не вносится, то значение соответствующей характеристики у этой программы принимается равным нулю. Внесение таких поправок, по существу, приводит лишь к изменению числа характеристик,

по которым и производится суммирование, с n до

( n + k ). То есть переобозначив n * = n + k , мы сно-

ва получим формулу (1):

m

C 0 =¹ Z m , = 1

A

Z x ij ^to i

A M max i ,

^ n*. xi0 ®i i=1 max i ’

в которой не вносятся изменения в значения характеристик и их весов для характеристик с i ∈ [1, n ].

Разработанная математическая модель может быть использована при реализации экономически эффективной инновационной политики хозяйствующих субъектов.