Математическая модель процесса экструзии зерновых культур при неизотермическом течении их расплава до температуры начала реакции Майяра

Методы

Для повышения продуктивности крупного рогатого скота (КРС) необходимо увеличить в сыром протеине долю защищенного белка, т. е. белка, устойчивого к воздействию ферментов микрофлоры и неспособного к распаду на составляющие – аммиак и углеродную цепочку [2, 7, 9, 11].

Отличительной особенностью моделирования процесса экструдирования зерновых культур при производстве комбикормов с защищенным белком для крупного рогатого скота является то, что смесь белка и редуцирующих сахаров нагревают до температуры начала реакции Майяра, т. е. до 120–125 °C, не допуская при этом ее развитие [1, 5, 6, 8, 10, 13, 14]. Баротермомеханическая обработка исходных компонентов в экструдере позволяет поучить комбикорма с защищенным белком.

При выборе математической модели были выбраны следующие ограничения и допущения: течение движущейся вязкой среды принимается ламинарным и установившимся; силы инерции и гравитации по сравнению с силами трения и давления настолько малы, что ими можно пренебречь; вязкая среда (расплав) представляет собой несжимаемую жидкость, характеризующуюся постоянными теплопроводностью и температуропроводностью; изменением теплопроводности в продольном направлении пренебрегали в связи с тем, что конвективный перенос теплоты в направлении течения выше, чем переноса теплоты теплопроводностью; теплопередача в направлению перпендикулярном течению расплава происходит только за счет теплопроводности;

Математическая модель неизотермического течения расплава зерновых культур включала:

уравнения движения р Г д vx     д vx     д vx     д vx + v    + v    + v _  дp —--- Г да xx да +--yL да zx L + р^г ( дт     дx   у ду     дz у дx ( дx ду дz x р Г д vy     д vy     д vy     д vy + v    + v    + v L дp ( да xy да + __Л да + _zL I+рд„ (дт     дx   у ду     дz )    ду ( дx ду дz Г дv7      дv7      дv7      дv7 ^ _  дp даxz да да77 Л р + vx     + v„     + v7 +---yL + рд2 (дт     дx   у ду     дz ) дz v дx ду дz у уравнение неразрывности

др   др    др   др

--+ v--+ v--+ v — дт     дx   у ду     дz

= - р

Г д vx   д vy   д vz)

x ^y z

( дx   ду   дz у уравнение энергии (теплового баланса)

р с р

д T    д T

— + v. — + vy дт     дx у

д T д T ) — + vz — I ду дz )

(дqx ,дqy ,дqz) т(др) 11— T

(дx   ду   дz )   (д T )

Г дv_x    ^д v y   д v_z )

+    +     I —

( дx   ду   дz )

—

^ xx

(

д v_x

^{+ а} уу д x

д v y

⁺ ^ zz д у

д v

д z

—

^ x»

^Г д v_x   ^{д v}y )

+     I + ^ zx

( ду   дx )

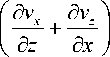
yz

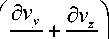
д z    д у )

Результаты и обсуждение

С учетом ранее принятых допущений уравнения неразрывности (1), движения (2) и энергии (3) можно упростить, так как компоненты течения в направлении одной или двух осей координат можно считать несущественными. Для неизотермического течения расплава в кольцевом канале экструдера значимыми являются только компоненты скорости в направлении оси x, а градиенты скорости и температуры имеют ненулевые значения только в направлении оси у. Это означает, что члены уравнений (1)-(3) с компонентами vy, vz и их производными по координатам x и z можно пренебречь.

Поэтому уравнение движения (1) [4] с учетом того, что дvx / дх = 0, так как движение является установившимся; vSvх / дх = 0, так как v = 0 ;  vz Svх / дz = 0, так как  vz = 0 ;

д^ / д х = 0 , так как нормальными напряжениями вследствие деформации сдвига пренебрегаем; да_и / д z = 0 , поскольку ширина кольцевого канала B значительно больше высоты кольцевого канала H , то влиянием боковых стенок на величину напряжений сдвига о_хх пренебрегаем;

pg_x = 0 , так как влиянием сил гравитации пренебрегаем, можно записать следующим образом

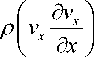
дp  доух дх ду

Уравнение неразрывности (2) [4] с учетом того, что др / дх = 0 - так как плотность постоянна и не меняется со временем; д / ду (pv,) = 0 - так как  vy = 0 ; д / дz(pvz) = 0, поскольку vz = 0;    если    член    уравнения(2)

Учитывая, что о = о_ух и q_y = —Лд Т / д у (закон

Фурье), имеем:

, д (д т )

Л — — =— дх ^ дх ) у ду

Уравнения (5–8) дополним начальными условиями vx0 = vx (х, у ,т = 0), vyo = vy (х, у,т=0) ’             (9)

Т, = Т ( х , у ,т = 0 )

и граничным условием по температуре: при прилипании расплава к стенкам канала тепловой поток в слое, прилегающем к стенке, определяется следующей формулой

5 T ) = _Bi ^Т к ^{— Т} т .         (10)

(ду J         § ст

Температура расплава, контактирующего со стенкой, принимается равной температуре стенки, то есть T к = T ст .

Вязкость зернового расплава при неизо- д / дх(pvx ) = 0 = рдvx / дх + vx / др / дх, а в нем

v_x / др / д х = 0 - так как р = const, то из него сле

дует, что pSv_х / д х = 0 и поэтому дv_x / д х = 0 .

термическом течении его в витках экструдера описывается уравнением в виде обобщенного степенного закона [4]

Принимая допущение о несжимаемости расплава (т. е. о постоянной плотности расплава), левая часть уравнение неразрывности (2) становится равной нулю, и оно приводится к виду:

( 1) m ( дvv | m о = —  —- yx

^ ф ) ^ д у }

,

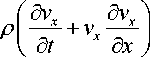
д p д х

дт yx

. д у

Решая совместно упрощенные с учетом принятых допущений уравнение неразрывности (4) и уравнение движения (5), получаем

где ф - эффективная вязкость расплава при начальных условиях; m – постоянных коэффициент расплава зерновых культур.

С учетом уравнений (8) и (11) изменение температуры расплава по высоте канала шнека описывается следующим уравнением

^д Р   ^да ух ₀

д х д у

_д(д Т б у W

Ф ( д p \ Л (д х }

у^т +¹

Таким образом, для уравнения энергии (5) были приняты следующие упрощающие допущения как течение является: д Т / д t = 0 - так установившимся; v д Т / д у = 0 - так как v _y = 0; v₇д Т / д z = 0 - так как v_z = 0;   дq_x / д х = 0 -

Z                                                             —4           х вследствие того что Т # f (х) ^ qx = 0; дqz / дz = 0 - так как дТ / Sz = 0; по условиям

Интегрируя уравнение (12) и учитывая, что при у = 0 ( д Т / д у ) (профиль температуры по высоте канала шнека является симметричным),

получаем

(^ т )

(бу }

/ - х m +1   _m+2

Ф ( д p ] у

Л \д 5х } m + 2

задачи предполагается, что все члены уравнений (1)-(3), содержащие n_z и v _y и их производные

по x и у , равны нулю.

После упрощения уравнения (5) получаем

Интегрируя уравнение (13) и определяя постоянную интегрирования, получаем

ф( m ^{+ 1} (0,5 HY ^{+ 3} — у^{т + 3}

Т = Т_и + ^Ф I ^ p I         )----—, (14)

Л (д х }    ( m + 2) ( m + 3) ^{v 7}

0 =

^д q y

—

д у

до xy

д v_x д z

где Т ст – температура стенки, ℃; x, y – координаты, м; Н – высота канала шнека, м; λ – теплопроводность расплава, Вт / (м×К).

Однако, учитывая, что теплота уносится вместе с потоком расплава, т. е. необходимостью учитывать передачу теплоты конвекцией, а также принимая во внимание закон теплопроводности Фурье и уравнение (11), оконча- тельно получаем f d Т

P ^CP v x I V V d x

.^{9 2} T

= <   + n ⁽ y )

d y

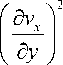
В уравнении (15) член в левой части уравнения описывает конвективную теплопередачу в направлении x, первый член в правой части уравнения – теплопередачу в направлении y за счет теплопроводности, и второй член в правой части уравнения – диссипационную энергию вязкого течения за счет существования градиента скорости в направлении y.

Для решения системы уравнений движения (4) и энергии (15) с учетом конвективной теплопередачи был использован численный метод конечных разностей, сущность использования которого заключалась в том, что рассматриваемая область (в данном случае канал экструдера) разбивается на расчетные ячейки с помощью сетки. Сетка состояла из прямоугольных ячеек с постоянным шагом между узлами, которые точно лежат на границах области интегрирования. При этом дифференциальные уравнения преобразовывались в разностные уравнения путем замены производных в точке конечными разностями по границам ячейки [3, 4, 12, 15–20].

Это означает, что касательная в точке заменяется хордой. Тангенс угла наклона касательной, который соответствует частной производной, заменяется тангенсом угла наклона секущей, то есть конечно-разностным отношением. Такие разностные схемы аппроксимируют производные более точно, чем так называемые граничные схемы – конечно-разностные схемы для передней или задней границы и точки внутри расчетной области [4]. Центральная разностная схема может быть построена, только если доступны узлы сетки по обе стороны от текущего (центрального) узла. Если точка сетки х п лежит на границе или так близко к ней, что точки сетки по другую ее сторону не существует, то производная аппроксимируется с помощью передней или задней разностных схем (соответственно с шагом вперед или назад):

Порядок решения математической модели (5)–(15) рассматривается на равномерной сетке. С этой целью разобьём область D = {0 < X < 1, 0 < Y < 1} на сетку с шагом hx и hY по переменным X и Y соответственно, с размерностью 13x17.

Для решения математической модели процесса экструзии зерновых культур при неизо-

Pascal 7,0. Исходные данные для расчета приведены в таблице 1.

Таблица 1.

Исходные данные для расчета процесса экструзии зерновых культур при неизотермическом течении их расплавов

Table 1.

Initial data for calculating the process of extrusion of grain crops in the non-isothermal flow of their melts

Переменная Variable Значение Value Шаг, м Step, m 0,0180 Глубина винтового канала, м Screw channel depth, m 0,014 Диаметр шнека, м Screw diameter, m 0,0220 Зазор между корпусом и шнеком, м Clearance between body and auger, m 0,0005 Частота вращения шнека, 1/с Screw speed, 1 / s 1,0000 Удельная теплоемкость продукта, Дж / (кг×К) Specific heat capacity of the product, J / (kg × K) 1590,0000 Плотность расплава продукта, кг/м3 Density of product melt, kg / m3 1270,0000 Коэффициент теплопроводности, Вт / (м×К) Thermal conductivity coefficient, W / (m × K) 0,2210 Вязкость, Па×с Viscosity, Pa × s 20000,0000 Избыточное давление, МПа Overpressure, MPa 4,5000 Начальная температура продукта, ℃ Initial product temperature, ℃ 20,0000 Температура стенки винтового канала, ℃ Screw channel wall temperature, ℃ 135,0000 Внутренний диаметр корпуса, м Inner diameter of body m 0,0225 Угол подъема винтового канала рад The angle of elevation of the screw channel is rad 0,2379 Угловая скорость (Vо) м/с Angular velocity (Vo), m / s 0,0660 Скорость по оси Z (Wz), м/с Z-axis speed ,(Wz) m / s 0,0641 Скорость по оси X (Wх), м/с X-axis speed, (Wx) m / s 0,0155 Число Рейнольдса Reynolds number 6,4 Е-0005 Число Эйлера Euler's number 8,80 Е + 0005 Число Эккерта Eckert number 1,79 Е-0008 Число Пекле Peclet number - термическом течении их расплавов составлена программа на алгоритмическом языке Turbo

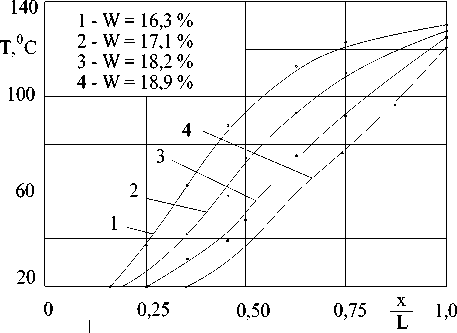
Рисунок 1. Изменение температур расплава зерновых культур по относительной длине рабочей камеры экструдера при различной начальной влажности зерновых культур

Figure 1. Changes in the melt temperatures of grain crops along the relative length of the working chamber of the extruder at different initial moisture content of grain crops

Учитывая тот факт, что повышение температуры расплава зерновых культур происходит за счет эффекта диссипации, т. е. преобразования механической энергии в тепловую за счет сил трения, то максимальная температура расплава наблюдается у поверхности шнека. Температура расплава у неподвижной стенки корпуса рабочей камеры может быть ниже, чем у шнека, на 10 ℃. Температура расплава в пристенной зоне (у боковых стенок корпуса рабочей камеры) возрастает, что вызвано влиянием эффекта охлаждения расплава в центральной части канала вследствие адиабатического расширения.

Сравнительный анализ расчетных значений температуры по модели (5)–(15) с аналогичными моделями других авторов [3, 4] показал, более высокую точность описания поля температур расплава при его неизотермическом течении в экструдере: среднеквадратичное отклонение не превышало 12,7% (рисунок 1).

Заключение

• 1.    Получена неизотермическая математическая модель процесса экструзии зерновых культур при температурах начала реакции Майяра, т. е. до 120–125 ℃, которая позволяет выявить характер изменения температуры по длине экструдера.

• 2.    Сравнительный анализ результатов численного решения и экспериментальных данных показал хорошую сходимость: среднеквадратичное отклонение не превышало 12,7%, что позволило сделать вывод о возможности получения экструдата с защищенным белком и использования полученной модели при разработке и проектировании экструдеров.