Математическая модель процесса коэкструдирования пищевых масс

В работах [1, 2] рассмотрен механизм и физическая картина получения комбинированных фаршевых изделий методом коэкс-трузии. В данной работе будет представлена математическая модель данного процесса.

Процесс формирования готовой продукции происходит в камере коэкструзион-ной насадки машинной системы Vemag893.

Камера формирования (рисунок 1) представляет собой полость цилиндрической формы, куда подается фаршевая оболочка. Коаксиально в данную полость подается начинка через кольцевой цилиндрический канал с клапаном, регулирующим подачу. Внизу камеры формирования установлена диафрагма с ножом в виде лепестков.

Рисунок 1 – Нижняя часть коэкструзионной насадки

1 – насадка; 2 – начинка; 3 – клапан; 4 – оболочка; 5 – камера формирования; 6 - диафрагма

Процесс формирования готового изделия связан с началом раскрытия ножей (лепестков) диафрагмы. По мере раскрытия диафрагмы поднимается клапан, связанный

Зарудный В.А., 2013

с пневматическим исполнительным механизмом, и по цилиндрическому кольцевому каналу внутрь оболочки выдавливается начинка. Формирование готового продукта связано с полным раскрытием и закрытием диафрагмы и клапана.

На рисунке 2 схематично представлено движение начинки и оболочки в камере форми

рования. С индексом 1 связаны величины, характеризующие начинку, с индексом 2 - оболочку.

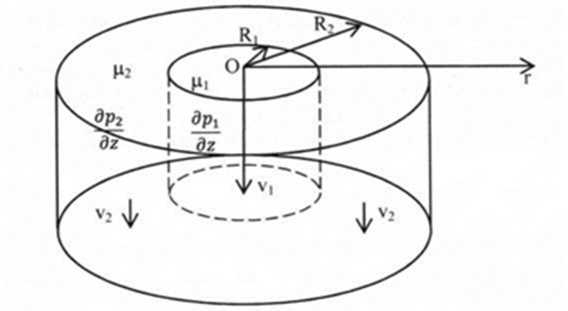
Рисунок 2 - Схема движения начинки и оболочки в камере формирования

За основу математической модели возьмем уравнение Навье-Стокса в цилиндрических координатах для движения очень вязких жидкостей [3] в трубе:

равную нулю.

Окончательно получаем обыкновенное дифференциальное уравнение:

Эр

Эt

i ЭР + ^ / Э² v + 1 Эг \ р Эг      Эг ²    г Эг

v ^ T U + ”Т ^{+ а} = 0         (5)

аг2   г аг уравнение для удобства интегрирования, представим в виде:

где v(r, t)- скорость, р - плотность, — — градиент давления, v - кинематическая вязкость.

Стационарная задача (^ = 0) коаксиального движения в трубе двухслойной жидкости при открытых клапане и диафрагме ранее была решена [4]. При решении нестационарного уравнения (1) используем зависимость градиента давления, меняющегося со временем по закону [5]:

- ^1Эр = а |sin(^t)| ,        (2)

р Эг а скорость представим как:

v(r,t) = |sin(wt)| •U(r),       (3)

Подставляя (2) и (3) в (1) и выделяя временную часть, получаем:

где U =

— (r—) + — = 0, аг аг v

( U i (r), 0 i ,

(U₂(r), R i 2,

а граничные условия:

f  U i (R i ) = U 2 (R i ),

U 2 (R 2 ) = 0,

R i V

dU t | ^аг R_t

au

= ^^ ,

a2u vau

a+v—7+^— dr2 г dr

MU

= |ct^(wt)|.

Уравнение (4) может иметь решение, если правая его часть равна постоянной величине. В нашем случае примем постоянную

где Ц 1 , ц₂ - динамические вязкости.

Решение уравнения (6) с условиями (7) будет иметь следующий вид:

— т² + С_А ln r + С₂,

4vt         i           2'

— r² + C₃ In r + C₄.

4V2         3          4

где C_i = 0 - из условия конечности скорости на оси трубы;

С₃ определяется, исход из третьего условия (7), С₄ - из второго, С₂ - из первого.

Г

С 2

1 dp i

4^_i dz

Rl +

1 ЭР 2

4^ 2 dz

Rl +

R² / dp i

2 к dz

—

dpr )'" ^R 1

^{1 9}P 2 R l

—

R l /ЭУ1

2 V dz

—

^ Ь R2-

V

C3

R

. 2

l

/ ^d p l к dz

—

®-

С 4 = ^— ^t^

+

R^j / dp i

2 к dz

—

at)'" 4

dp,    dp2    .

В (9) "d^¹ и "dz " - амплитуды градиентов давлений.

Окончательный вид нахождения скорости истечения жидкостей определяется подстановкой (8) и (9) в (3).

Объем жидкости (фарша), протекающий в единицу времени через поперечное сечение трубы, определим по формуле:

Q = 2 /J^1 2nw1dr + jRR2 2Hrv2dr). (10)

Коэффициент 2 получаем путем усреднения за время одного цикла функции |sin(^t)|:

т

-J02|sin[^t)|dt = -.              (11)

Среднюю скорость течения можно опре- делить по формуле:

Q

-R2"

Коэффициенты С 2 , С 3 , С 4 , обозначенные в уравнениях (9), находят, исходя из известных параметров процесса и конструктивных размеров коэкструзионной насадки.

В заключение, следует сделать некоторые выводы:

• -    получены уравнения, описывающие движение в цилиндрической трубе двух соприкасающихся вязкопластичных жидкостей;

• -    определены выражения для постоянных коэффициентов уравнений движения, зависящих от параметров процесса и конструктивных размеров коэкструзионной насадки.