Математическая модель процесса обеспечения качества технического сервиса
Автор: Редреев Г.В.
Журнал: Вестник Омского государственного аграрного университета @vestnik-omgau
Рубрика: Технические науки
Статья в выпуске: 3 (31), 2018 года.
Бесплатный доступ
Для своевременного выполнения полевых работ в АПК необходимо обеспечить определенный уровень безотказности сельскохозяйственных машин. Оценку безотказности наиболее целесообразно проводить на основе комплексного показателя - коэффициента технического использования. Величина коэффициента технического использования зависит от качества технического сервиса машин. Обоснованные практические рекомендации достижения требуемой величины этого коэффициента могут быть предложены на основе математического моделирования процесса обеспечения качества технического сервиса. Предлагается представить коэффициент технического использования в виде произведения его базового значения на коэффициент качества. Коэффициент качества определяется как произведение степеней соответствия: выполненных объемов работ технического сервиса - требуемым объемам; периодичности технического обслуживания (ТО) - нормативным значениям; технологий ТО и ремонта - обслуживаемым машинам; квалификации исполнителей технического сервиса - технологиям ТО и ремонта; квалификации исполнителей технического сервиса - обслуживаемым машинам...
Безотказность, коэффициент технического использования, коэффициент качества технического сервиса, степень соответствия, коэффициент разномарочности парка машин
Короткий адрес: https://sciup.org/142216234
IDR: 142216234 | УДК: 631.372
Текст научной статьи Математическая модель процесса обеспечения качества технического сервиса
При реализации процессов технического сервиса возникает задача обеспечения уровня качества, ожидаемого потребителем услуг технического сервиса. Поскольку качество технического сервиса не может быть проверено непосредственно по завершении
конкретной услуги, а выявляется по фактической безотказной наработке сельскохозяйственной машины или агрегата, необходима методика или процедура подтверждения уровня качества технического сервиса.
Уровень безотказности удобно оценивать посредством коэффициента технического использования, представляемого в виде произведения его базового значения на коэффициент качества технического сервиса: треб б
К ти — К ти К ти К ц , (1)
где Кби - базовое значение коэффициента технического использовании; Км - коэффициент качества технического сервиса, определяемый по зависимости n
K , = п А , (2)
при i = 1-5. Степени соответствия: , - выполненных объемов работ технического сервиса - требуемым объемам; , - периодичности ТО - нормативным значениям; , -технологий ТО и Р - обслуживаемым машинам; ,4 - квалификации исполнителей тех нического сервиса - технологиям ТО и ремонта; , - квалификации исполнителей технического сервиса - обслуживаемым машинам.
Требуемый объем работ по техническому сервису определится из выражения
K,L wtc- = Е amArSt т , (3)
TC k k l l k,l=1
где A k - обслуживаемые агрегаты, k = 1 + K ; MA k - количество машин в k -м агрегате; S i - количество подсистем (узлов, сборочных единиц) в машине, l = 1 + L ; т - длительность обслуживания l -й подсистемы (узла, сборочной единицы).
В соответствии с разработанным концептуальным проектом системы технического сервиса [1], объем работ, выполняемый группой работников сервисной службы, должен соответствовать требуемым объемам работ при техническом сервисе машин агрегатов:
N K , L
, i Е N . k N t — Е A k MA k S Ti , i = 1 k , l = 1
где N 1 - число работников сервисной службы; t - продолжительность технического обслуживания, ч; k N - поправочный коэффициент, учитывающий снижение продолжительности технического обслуживания при работе группы работников сервисной службы.
Вероятная восстанавливающая способность применяемого при технического сервисе перечня технологий ТО и ремонта определится из зависимости [2]:
M
R = Е TX j S j , (5)
j = 1
где TX j - j -я технология из общего перечня технологий ТО и ремонта, j = 1 + M ; 5 ] - степень восстановления работоспособности (наработки) j -й технологией.
В результате анализа отношений целенаправленной деятельности установлено, что при реализации выделяемых групп операций технического обслуживания и ремонта (ТО и Р) происходит увеличение безотказности технических устройств на определенное время, соответствующее увеличению наработки агрегата. В смысле безотказности как свойства сохранения работоспособности, величина восстанавливаемой наработки должна быть сравнена с требуемым временем безотказной работы [3-4].
ПФАКТ
^ 2 П Т-РЕБ .
Применяемые типы работ ТО и Р должны соответствовать процессам в узлах (подсистемах, сборочных единицах) машин агрегатов [5]: M K , L
И У TX j } ■ { Z 'MAS. } • (7)
j = 1 k , l = 1
Значения степени соответствия технологий ТО и Р процессам в подсистемах обслуживаемых машин могут быть определены методом экспертных оценок либо ранжированием [6-8].
При этом компетенции исполнителей работ технического сервиса должны быть достаточны для реализации технологий ТО и ремонта:
NM
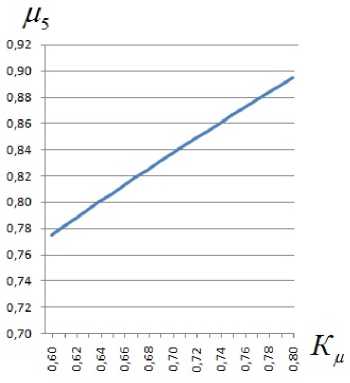
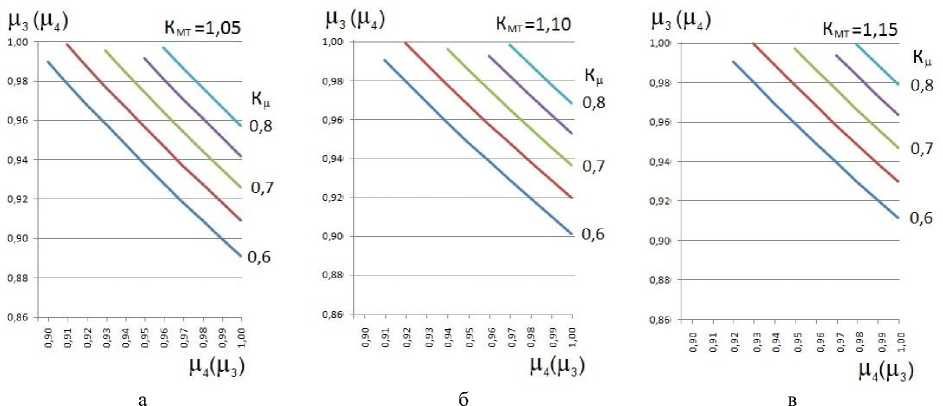
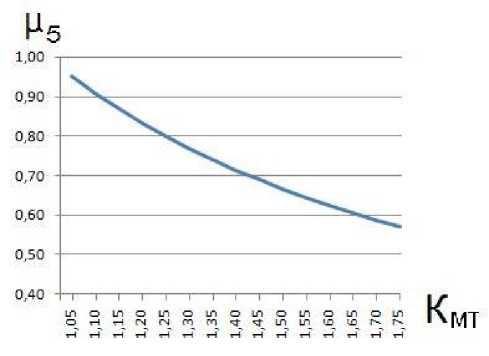
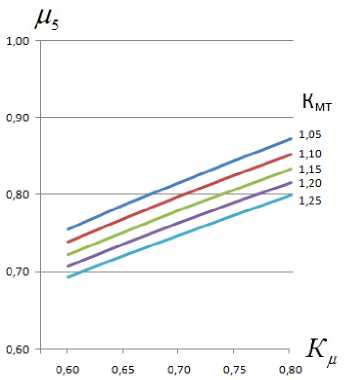
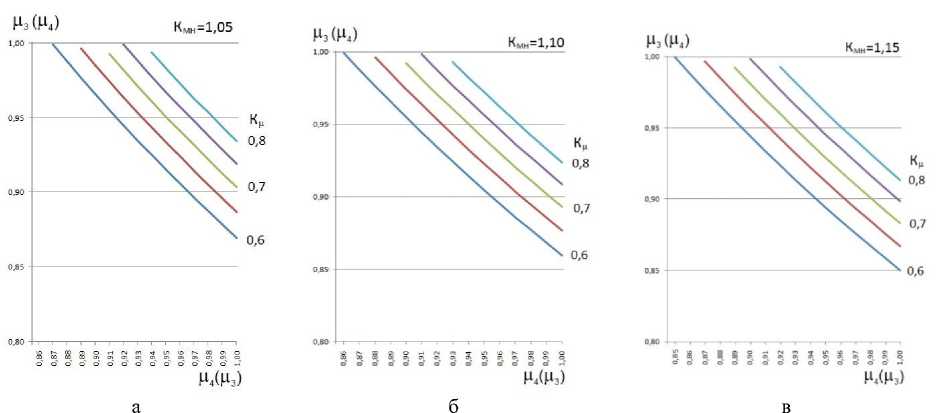
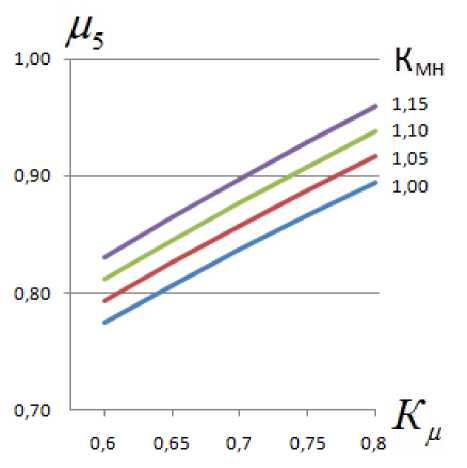
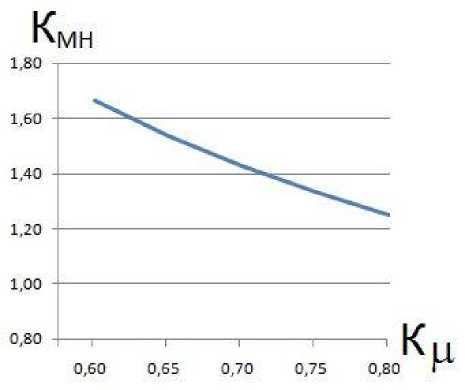
И. У NK} « i=1 где Ni - i-й исполнитель ТО и ремонта; Ki - компетентность i-го исполнителя. Перечень работ, потенциально выполняемых исполнителями технического сервиса, должен быть достаточен для обслуживания определенного вида МТА [9-10]: NK И, Z NK >Z A' MA-' •(9) i=1 k, l=1 Методы Для моделирования системы технического сервиса предлагается следующее ана- литическое описание ее состояния: NK, L М-Z N,--n ■ t = Z a- - MA. - Si Ti;(10) i=1 k, l=1 ПФАКТ = М2 ПТРЕБ ;(11) MK Из Z TXj = Z MA. - Si;(12) j=1 k, l=1 NM М4 Z NKi =Z TXj ;(13) i=1 NK И Z NK = Z ma. - Sl •(14) i=1 k, l=1 Задача выполнения требуемого объема работ по ТО при условии снижения длительности простоя машин решена с учетом обеспечения нормативной периодичности ТО [11]. Для обеспечения функционирования системы технического сервиса является важным установление рационального соотношения квалификации исполнителей технического сервиса, применяемых технологий и характеристик обслуживаемых машин. Примем для дальнейших рассуждений ц 1 = 1,0 и ц2 = 1,0. Это означает, что работы по ТО выполняются в полном объеме, периодичность ТО всех подсистем не превышает значений, указанных в нормативной документации на сельскохозяйственную технику. В таком случае математическая модель будет выглядеть следующим образом: MK Из Z TX, = Z ma. - Sl;(15) j=1 k, l=1 NM и. Z NK=Z TX;(16) i=1 NK и, Z NiK = Z MAk - Sl •(17) i=1 k, l=1 Подставив выражение для ΣТХ из (16) и выражение для Σ(МА⋅ S) из (17) в выражение (15), получим: µ3⋅µ4 = µ5.(18) Тогда (, ,4)2 = К,(19) или ,2 = К, .(20) Следовательно, минимальные значения отдельных степеней соответствия определятся: , а Кк"„(21) /<М) = -,-.(22) ,3(,4) Результаты В соответствии с данными СибИМЭ и результатами анализа практики, фактическое значение коэффициента технического использования находится в пределах 0,55 ± (0,02–0,03). Для целей теоретического исследования можно предложить следующие пределы изменения базового значения Кб и соответствующих минимальных значений коэффициента качества Кµ: Си = (0,7 - 0,9), Кµ = (0,8 – 0,6). Определим допустимые пределы изменения составляющих качества µi. Результаты расчетов для Кµ = (0,8 – 0,6) графически могут быть представлены следующим образом (рис. 1): М4(Мз) Рис. 1. Минимальные расчетные значения µ3, µ4 Исходя из возможного минимального значения µ3 (или µ4) на оси абсцисс, определяется минимальное значение µ4 (или µ3) на оси ординат при различных значениях Кµ – от 0,6 до 0,8 с шагом 0,1. Значение µ5 определится как произведение µ3 ⋅ µ4. Графическое изображение зависимости значений µ5 от Кµ представлено на рис. 2. Для того чтобы качество технического сервиса повысилось на 10%, необходимо повысить на 5% какую-либо одну из степеней соответствия: применяемых технологий обслуживаемым машинам, квалификации исполнителей применяемым технологиям или квалификации исполнителей обслуживаемым машинам. Того же эффекта можно добиться, повы- Рис. 2. Зависимость значений степени соответствия квалификации исполнителей обслуживаемым машинам µ5 от коэффициента качества Кµ сив на 2,5% степень соответствия применяемых технологий обслуживаемым машинам и степень соответствия квалификации исполнителей применяемым технологиям. Справедливо и обратное: снижение на 5% любой из степеней соответствия приведет к снижению на 10% качества технического сервиса [12]. Совокупность зависимостей (15)–(17) является общим случаем постоянного соотношения квалификации исполнителей, технологий сервиса и конструкций машин. Воз- можны, кроме представленного случая, семь временных вариантов производственных ситуаций. Рассмотрим три из них. Вариант 1. Применяемые технологии могут быть использованы для обслужива- ния разномарочного парка машин. MK µ3∑TXj≥∑MAk⋅Sl;(23) j=1 NM µ4∑NiKi=∑TXj;(24) i=1 NK µ5∑NiKi=∑MAk⋅Sl.(25) i=1 Для определения значений µi необходимо в зависимости (23) перейти к строгому равенству: MK µ3∑TXj =КМТ∑MAk⋅Sl ,(26) j=1 где КМТ – коэффициент разномарочности парка машин по применяемым технологиям. Очевидно, что КМТ > 1. Подставив выражение для ΣТХ из (24) и выражение для Σ(МА⋅ S) из (25) в выражение (26), получим: µ5 =µ3⋅µ4. (27) КМТ Соответственно: Кµ ^ К к МТ М3(М4) = М5 ' КМТ M Мз) Результаты расчетов для различных значений КМТ представлены на рис. 3. Рис. 3. Зависимости минимальных значений µ3 и µ4 Анализ показывает, что с ростом коэффициента разномарочности парка машин по применяемым технологиям степень соответствия технологий обслуживаемым машинам и степень соответствия квалификации исполнителей применяемым технологиям долж- на увеличиваться. Из выражения (27) следует: М ^ к КМТ Графически зависимость представлена на рис. 4. Рис. 4. Зависимость минимальных значений коэффициента µ5 от коэффициента разномарочности парка машин по применяемым технологиям Чтобы обеспечить обслуживание парка машин, разномарочного по применяемым технологиям, необходимо снижать степень соответствия квалификации исполнителей технического сервиса обслуживаемым машинам в К раз (рис. 5). Вариант 2. Квалификация исполнителей позволяет расширить перечень применяемых технологий технического сервиса. Квалификация исполнителей должна быть достаточна для реализации новых технологий технического сервиса. MK, L № £ ™,=£ MAk ■ Si;(31) =1 k, l=1 NM № £ NK^£ TX,;(32) І=1 NK № £ NK = £ MAk' Si.(33) i=1 k, l=1 Рис. 5. Зависимость минимальных значений коэффициента µ5 от коэффициента качества технического сервиса при различных значениях коэффициента разномарочности парка машин по применяемым технологиям Для определения значений µi необходимо в зависимости (30) перейти к строгому равенству: NM №4 £ NK = Ктн £ TXj, (34) i=1 j=1 где КТН – коэффициент новизны применяемых технологий технического сервиса. Очевидно, что КТН > 1. Аналогично, подставив выражение для ΣТХ из выражения (34) и выражение для Σ(МА⋅S) из выражения (33) в выражение (31), получим: и, = ^a-Sa ; (35) КТН и,=AКи-,; (36) КТН Из(И4) = ^ААКТН-. (37) И4( Из) Из выражения (35) следует: И, А -!-. (38) КТН Выражение (38) соответствует выражению (30). Таким образом, зависимости значений µi для различных величин КТН будут аналогичны зависимостям для различных величин КМТ. Чтобы освоить новые технологии технического сервиса, необходимо аналогично снижать степень соответствия квалификации исполнителей технического сервиса обслуживаемым машинам в К раз. Вариант 3. Квалификация исполнителей должна быть достаточна для обслуживания разномарочного парка машин. MK №з E TXj = ^ MAk ■ Si;(39) j=1 k, l=1 NM №4 E NK^E TXj;(40) I=1 NK № E NKi^E MAk ■ S .(41) i=1 k, l=1 Для определения значений µi необходимо в зависимости (39) перейти к строгому равенству: NK № E NKi= Кмн E MAk' Si,(42) i=1 k, l=1 где КМН – коэффициент разномарочности парка машин по квалификации исполнителей. Очевидно, что КМН > 1. Подставив выражение для ΣТХ из выражения (40) и выражение для Σ(МА⋅ S) из выражения (42) в выражение (39), получим: Соответственно КМН №5 №з • №4 №5 = 4 К№КМН №3(^4) = №5 КМН №4(№3^ Результаты расчетов для различных значений КМН представлены на рис. 6 и 7. Рис. 6. Зависимости минимальных значений µ3 и µ4 при КМН = 1,05–1,15 При обслуживании разномарочного парка машин по квалификации исполнителей необходимо допускать некоторое снижение степени соответствия технологий обслуживаемым машинам и степени соответствия квалификации применяемым технологиям. Рис. 7. Зависимость минимальных значений коэффициента µ5 от коэффициента качества технического сервиса при различных значениях коэффициента разномарочности парка машин по квалификации исполнителей Из выражения (44) следует (рис. 8): КМН 1 ≤ Кµ Рис. 8. Влияние коэффициента качества технического сервиса Кµ на величину коэффициента КМН разномарочности парка машин по квалификации исполнителей Качество технического сервиса увеличивается при снижении разномарочности парка машин по квалификации исполнителей. Выводы Произведено аналитическое описание условия функционирования системы технического сервиса как совокупности соответствий объемов базисных понятий. В качестве оценки безотказности техники АПК принят коэффициент технического использо- вания, представленный как произведение базового его значения и коэффициента качества технического сервиса. Аналитически коэффициент качества технического сервиса представлен как произведение степеней соответствия объемов базисных понятий. Определены взаимосвязи составляющих качества технического сервиса для различных условий функционирования систем технического сервиса: установлено, что коэффициент качества технического сервиса находится в квадратичной зависимости от степени соответствия квалификации исполнителей технического сервиса конструкциям обслуживаемых машин; степень соответствия квалификации исполнителей технического сервиса конструкциям обслуживаемых машин численно равна произведению степеней соответствия квалификации исполнителей технического сервиса применяемым технологиям и применяемых технологий конструкциям обслуживаемых машин. При изменении производственной ситуации система стабилизируется вводом в математическую модель коэффициентов учета увеличения разномарочности, различающейся для технологий и для исполнителей технического сервиса, и новизны технологий. По истечении некоторого времени система технического сервиса возвращается в основное состояние. Omsk State Agrarian University named after P.A. Stolypin, Omsk A mathematical model of the process of ensuring the quality of technical service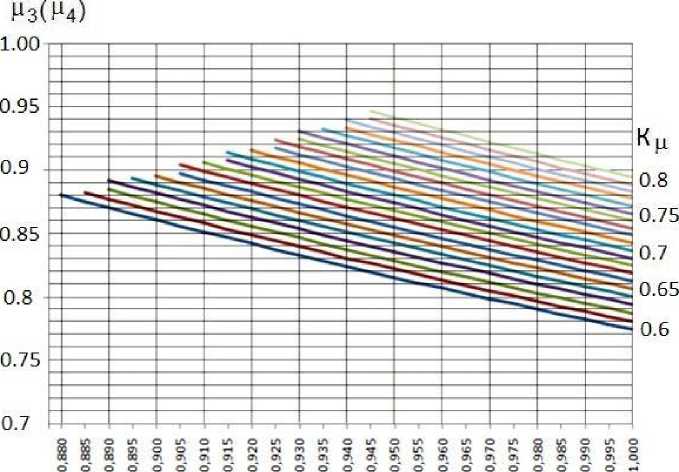
Список литературы Математическая модель процесса обеспечения качества технического сервиса
- Information System of Machines and Tractors Fleet Technical Service/G.V. Redreev, A.A. Luchinovich, E.I. Ustiyantsev, A.S. Laskin/Journal of Physics: Conference Series, Volume 1059, conference 1 -URL: http://iopscience.iop.org/article/10.1088/1742-6596/1059/1/012003.
- Байкельт Ф. Надежность и техническое обслуживание. Математический подход. Пер. с нем./Ф. Байкельт, П. Франкен. -М.: Радио и связь, 1988. -392 с.
- ГОСТ 27.002-89. Надежность в технике. Основные понятия, термины и определения. -М.: Изд-во стандартов, 1990. -39 с.
- Редреев Г.В. К вопросу о применении технологий ТО и ремонта при обеспечении работоспособности машинно-тракторных агрегатов/Г.В. Редреев//Современные проблемы науки и образования. -2014. -№ 5. -Режим доступа: www.science-education.ru/119-14864 (дата обращения: 11.07.2017).
- Мещеряков В.Т. Соответствие как отношение и принцип/В.Т. Мещеряков. -Л.: Наука, Ленингр. отд., 1974. -104 с.
- Бешелев С.Д. Математико-статистические методы экспертных оценок/С.Д. Бешелев, Ф.Г. Гурвич. -2-е изд., перераб. доп. -М.: Статистика, 1980. -263 с.
- Пытьев Ю.П. Возможность. Элементы теории и применение/Ю.П. Пытьев. -М.: Эдиториал УРРС, 200. -192 с.
- Редреев Г.В. Взаимодействие исполнителей ТО и ремонта при обеспечении работоспособности машинно-тракторных агрегатов/Г.В. Редреев//Современные проблемы науки и образования. -2014. -№ 2. -Режим доступа: www.scienceeducation.ru/116-12434 (дата обращения: 21.07.2018).
- Кэндэл М. Ранговые корреляции/М. Кэндэл//Зарубежные статистические исследования. -М.: Статистика, 1975. -216 с.
- Сковородин В.Я. Справочная книга по надежности сельскохозяйственной техники/В.Я. Сковородин, Л.В. Тишкин. -Л.: Лениздат, 1985. -204 с.
- Редреев Г.В. Обоснование процесса технического обслуживания тракторов группой исполнителей во время полевых работ: автореф. дис. … канд. техн. наук: 05.20.03/Редреев Григорий Васильевич. -Челябинск, 1996. -16 с.
- Редреев Г.В. Основы проектирования машин: учеб. пособие/Г.В. Редреев/Изд-во ФГОУ ВПО ОмГАУ. -Омск, 2009 г. -90 с.


