Математическая модель процесса обжарки каштанов перегретым паром

Для получения полной картины протекания процесса обжарки, инженерных расчетов и проектирования оборудования важно создание математической модели. Определение рациональных параметров обжарки дает возможность интенсифицировать процесс и снизить энергозатраты.

Рассмотрим математическую модель процесса обжарки перегретым паром плодов каштана европейского, разрезанных на кубики с размером a = 3…5 мм. Она может быть рассмотрена для слоя частиц, имеющих форму куба с эквивалентным диаметром d_экв . Принимая это допущение, эквивалентный диаметр частицы определяем по формуле:

3 ³ , (1) экв ч^ 4 _к ,( )

где а ч – линейный размер частицы каштана, м.

Основной задачей изучения теплопроводности и диффузии влаги является изучение пространственно-временного изменения температуры и влагосодержания или температурного поля и поля влагосодержания соответственно в объеме слоя частиц каштана.

Теплоноситель, перегретый пар, представляет собой среду процесса обжарки, температура которой принимается постоянной Т = 473 K. Частицы каштана в начале процесса обжарки имеют начальную температуру Т н , К, и влагосодержание u н , кг/кг, равномерно распределенные по объему частицы.

Рассматриваемый процесс обжарки частиц каштана является типичным нестационарным. В условиях взаимодействия частиц твердой фазы с теплоносителем изменяются концентрация влаги и температура в каждой частице как по координатам, так и по времени. Средняя по объему частиц концентрация распределяемого вещества, характеризуемая влагосодержанием, кг влаги/кг продукта, и температура в каждый момент времени определяются интегралами:

U ( т ) = - J U ( X, т ) dV ,

V ( V )

T ( т ) = - J T ( X, т ) dV , (2) V ( V )

где V - объем частиц, м 3 ; X = ( x , y , z ) - координата точки в объеме частиц; U - влагосодержа-ние, кг/кг; T - температура, K.

Поскольку распределение температуры и влагосодержания является постоянным по длине и ширине слоя продукта, то координата точки определяется ее высотой: X = x .

Рассмотрим процессы теплопереноса от перегретого пара к слою продукта и влагопере-носа, протекающего в обратном направлении.

Коэффициент диффузии влаги (коэффициент потенциалопроводности переноса влаги, коэффициент турбулентной температуропроводности), м2/с, вычисляется аналогично коэффициенту температуропроводности:

a

m

3^, cmP ’

где 3 m - коэффициент влагопроводности (тур-бул ентная теплопроводность), (ᴍ∙с)^-1; с m – коэффициент массоемкости, кг^-1.

Коэффициенты диффузии amи термо диффузии amT влажных тел связывает относительный коэффициент термодиффузии [1, 2]:

T

5 = a m a_m

Величины a_m и δ являются функциями влагосодержания и температуры [1, 2]. Рассмотрим частицу каштана как коллоидное капиллярно-пористое тело; связанное вещество жидкость – пар.

a — a + a , m mcap mk

TTT a — a + a у m    mcap    mk

5 -a + 5, • a ,

5   capap mmpap    k mk mcap mk

До достижения продуктом темп ературы 373 К (до перехода влаги из жидкого в газообразное состояние) удельная теплоемкость вычисляется по формуле:

c — c 0 + c 1 u 1 ,                    (8)

a после:

c — c 0 + c 2 u 2 ,                    (9)

где с 0 – удельная теплоемкость абсолютно сухого продукта, Дж/(кг∙К); с 1 – удельная теплоемкость пара, Дж/(кг∙К); с 2 – удельная теплоемкость воды, Дж/(кг∙К) (обозначение индексов: i = 1 – парообразная влага; i = 2 – жидкообразная влага).

При описании процесса обжарки каштанов были приняты следующие допущения: частицы каштана рассматриваются в виде куба; геом етрическая форма обжариваемого продукта постоянна; начальное распределение темпе- ратуры и влагосодержания по объ ему обжариваемого продукта постоянны; плотность потока теплоты и массы постоянны; разбиение на зоны позволяет достигать требуемой точности расчета температуры и влажности продукта.

Начальные условия:

T ( x , t )|^ — 0,0012 т ⁴ + 0,0807 т ³ - (₁₀) - 1,8278 т ² + 18,555 т + 295,39

u ( x , т ^ — 8 . 10 - 5 т ² - 0,0195 т + 0,6813 (11) ^T ( x - т ) , — 0 — T H (12) ^U ( x - ^Г )| _т „ ^— “ . ⁽¹³⁾

, d T

- 3—

Граничные условия третьего рода: для уравнения теплопроводности

— « ( T np - T n ) ( ¹⁴ )

x — X ( т )

d x

для уравнения массопереноса

- a , ^B!_x     — в ( T , - T . ) (15)

^d x x — X ( т )

где α – коэффициент теплоотдачи, Вт/(м²∙К); T пр , T п – температуры продукта и перегретого пара, К; β – коэффициент массоотдачи, м/с:

e—Nu^m, d экв

где Nu – критерий Нуссельта; d экв – эквивалентный диаметр частицы каштана, м.

Поскольку течение теплоносителя является ламинарным, то критерий Нуссельта определя ется по формуле:

Nu — 0,15Re 0, ³³ Pr 0,4 ³ Gr⁰ , ¹

Pr

Pr ст

£ i , (17)

где Re – критерий Рейнольдса; Pr – критерий Прандтля; Pr ст – критерий Прандтля для теплоносителя при температуре стенки; Gr – критерий Грасгофа; e l - коэффициент, зависящий от критерия Рейнольдса, линейного размера частицы и ее эквивалентного диаметра.

_ с и Pr — ^.^ ,

где с п – удельная теплоемкость перегретого пара, Дж/(кг∙К); μ п – динамическая вязкость перегретого пара, Па^с; 3 . - коэффициент теплопроводности перегретого пара, Вт/(ᴍ∙К).

Gr = gd^ Р п р п _А т ,          (19)

Рп где ρп – плотность перегретого пара, кг/м3; βп – коэффициент температурного расширения перегретого пара, K-1; ΔT – разница температур теплоносителя и стенки, K.

Полученная система уравнений (10-15) представляет собой математическую модель процесса обжарки каштанов.

Поскольку в процессе обжарки продукт изменяется в объеме, задачу (14-15) необходимо рассматривать, как задачу с подвижными границами [3, 4]. Вследствие усадки продукта высота его слоя h , м, изменяется в зависимости от времени τ , с, по следующему закону:

h = ( 2 - 10 - 6 т ² - 0,0121 т + 30,8 ) - 10 ^{- 3}. (20)

Влагоперенос парообразной ( i =1) и жидкообразной ( i =2) влаги описывается следующими соотношениями [1, 2]:

j = am.p0^u - amР0^T = -am.p0 (Vu + 5iVT) i = 1, 2,(21)

а суммарный перенос пара и влаги равен:

j = 1 ⁺ j 2 = ^{- a} m p 0 ^ u ^- a m P 0 ^{V T} =

= -amp (vu + 5VT)

Следовательно, система дифференциальных уравнений массопереноса будет иметь вид:

d U— p0 — = - div 11 + J1,(23)

дт дU— p0 — = -div J2 + J2,(24)

д т

Суммируя (23) и (24), получаем:

p0 — = - div j1 - div j2,(25)

дт

Подставив вместо j ₁ и j ₂ соответствующие выражения, получим:

p0 ?^ = ”^ Cam 1 p0V- + am 1 p0VT]+

⁺ div [ ^a m 2 p\ ^- + ^a m 2 p 0 ^{V T} ]

Дифференциальное уравнение переноса теплоты будет иметь вид:

c p 0 — = div ( AV T ) + Г 12 J 12 - £ cj V T , (27)

где r 12 – теплота парообразования, Дж/(кг∙К).

Источник жидкости J ₂ = J ₁₂ определяется из уравнения (25), для чего полагаем д - 1 /д т = 0 :

—

J 2 = J i2 = - J i =- div J 1 .          (28)

Следовательно:

д- cp0 — = di v (AV T) +

⁺ Г 12 div ( ^a m 1 p 0 ^{V -} + a m 1 p 0 ^V T ) ^- ^

i

— c j V T

Для зональной системы расчета [5], когда для каждого интервала (зоны) u и T коэффициенты переноса X , a_m i , a_{m 2}, a m 1 , a m ₂ полагаем постоянными, система дифференциальных уравнений тепломассопереноса будет иметь вид:

d^- = am v ² u + a^TT V ² T = am [v ² u + 5 V ² T ] (30) dт                      ^{L J}

-- = | a + a m 1 - 12 IV ² T + a m 1 - ¹² V ² u -

« т v c ; c             л n

\         -      - \     v T ⁽³¹⁾

-[ ( c 1 ^a m 1 ⁺ c 2 ^a m 2 ) ^V u ⁺ ( c 1 ^a m 1 ⁺ c 2 ^a m 2 ) ^{V T} ] ~

Так как перенос вещества происходит только в одном направлении, то градиент будет являться дифференциалом по координате x :

dud ² Td ²

= ^am    u ^{+ a}m    ^- = ^am

«т dx dx dT

« т

,       -12 | d -г a + am 1— I "TT - + am 1 c ; dx d2d2

—_ru + 5 —-T dx ²       dx ²

r 12 d ² cdx ²

u -

dT (33)

( c 1 ^a m 1

x du , _{T T} xdT _dx ⁺ c 1 ^am I ) , ⁺⁽ c 1 ^am 1 ⁺ cI ^amI j , dx                dx c

Дифференциалы, расписанные правые конечно-разностные отношения:	через
d- = - + 1 - - « т    N t	(34)
d- = -i + 1 - -i dx     N x	(35)
d2 - = - + 1 - 2T + - - 1 dx 2         A x 2	(36)
du _ u + 1 - u, « т    A t	(37)
d 2 u _ u , + 1 - 2 u , + u , - 1 dx 2         A x 2	(38)

Поставленная задача может быть решена методом конечно-разностной схемы, реализуемым через метод сетки. Это требует разработки программного модуля расчета, что позволяют сделать современные среды, применяемые для моделирования (Maple, MathCAD, Mathlab).

Используя приведенные выше переходы от дифференциальных уравнений к записи уравнений в конечно-разностной форме, исходные дифференциальные уравнения (7), (8) преобразуют к виду:

-

u n , к + 1

u n + 1, к ^- u n , к

'------- = а_т

A t

Tk+i- 2T к* T n, к + 1        n, к      n

- ² u , + u,

A x ²

T

+ a m

u n , к + 1

A x x

^{- 2} u n , к ⁺ u n , к - 1 a_m

A x ²

T n , к + 1 ^{2 1} n , к ⁺ T n

^{+ 5} am —-------

A x ²

T . , T n + 1, к

T и

A t

r_n ) T n , к + 1 — 2 T ,, к + T n , к - 1

a + am 1 — I-------71-------+ c )        Ax2

⁺ a m 1

Г 12 u n , к + 1 ^{- 2} u n , к ⁺ u n , к - 1 c         A x ²

В полученных дифференциальных уравнениях температура и влагосодержание представлены в безразмерном виде, т. е. определяются как отношение текущей величины к ее начальному значению (Т н = 293 К; и _н = 0,43 кг/кг).

На термодинамические характеристики процесса оказывает влияние температура продукта [1]:

a m = 2,1 . 10 - ¹⁵ T n³ , к               (43)

a m 1 = 0,3 . 10 ^{- 19} T n³_к            (44)

Зависимости коэффициентов температуропроводности а и теплопроводности X от температуры Т выведены эмпирически.

Значения теплофизических характеристик каштанов для интервала температур 293^353 К:

при и _н = 0,43 кг/кг:

Л = 0,137 + 0,00021;(45)

а = (4,08 + 0,00371) .10-8.(46)

при и _к = 0,04 кг/кг (обжаренный продукт):

Л = 0,084 + 0,00021;(47)

а = (3,9 + 0,00361) .10-8.(48)

—(c_Aa 1

1 m 1

⁺ c 2 a m 2

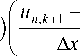
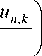
A x

c

,,

T n , к + 1

-Ci <2 T , + C^ T T --------— ----—----

1 m 12 v ' (Ax

где n - шаг разбиения по времени; к - шаг разбиения по координате.

После выражения из уравнений (39), (40) значений влагосодержания и температуры на

следующем шаге квантования по времени через предыдущий получим:

^u n , к + 1

и ,, = и , + a at------ n + 1, к      n , к      m

2a , +и , , n , к      n , к - 1

dx ²

t T n , к + 1 - 2T n , к + T n , к - 1

+am dt---------------- dx

T n + 1, к

= ^Tn , к

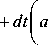
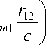
T n , к + 1 - 2 T n , к + T n , к - 1 dx ²

Коэффициент a m ₂ и относительный коэффициент термодиффузии 5 от температуры зависит незначительно [6], поэтому в расчетах они приняты постоянными: a m 2 = 0,4^10 " ⁶ м²/с; 5 = 1,149-10 " ³.

Влагосодержание оказывает незначительное влияние на термодинамические коэффициенты [7], которым можно пренебречь.

Метод конечно-разностной схемы в явном виде реализуется через метод сетки [3, 8]. Суть метода сетки заключается в том, что вся заданная пространственно-временная область разбивается на равные интервалы времени и пространства через выбранные интервалы дискретизации A t и A x , и затем находятся значения интересующего нас параметра в каждом узле сетки. Решение поставленной задачи требует представления исходного дифференциального уравнения в виде конечно-разностных отношений (39), (40).

Значения температуры и влагосодержания на каждом следующем шаге по времени вычисляются по схеме (рисунок 1).

Г 2 u n , к + 1 ^{- 2} u n , к ⁺ u n , к - 1

am 1--JI-------- c        dx

^- ( c 1 a m 1

. ( u n , к + 1 - u n , к M ^Tn , к + 1 - ^Tn , к ) dt

^{+ c} 2 a m 2 ) l — ’—, ---^ P----",----~

( dx ) dxc

- ( c 1 a m 1

T

⁺ c 2 a m 2

) (

Tn, к+1 - dx

T n , к | ( T n , к + 1 - T n , к ) dt ) dxc

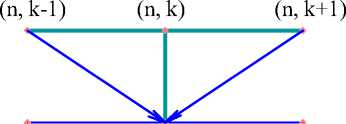
(n+1,k-1)    ( n +1,k)      (n+1,k+1)

Рисунок 1 - Шеститочечная явная схема

Задача (41 - 42) представляет собой краевую задачу тепло- и массопроводности с одной статичной и одной движущейся границей [2, 4] и решена с использованием функциональных преобразований методом конечных разностей [9]. Разработан программный модуль расчета процесса обжарки каштанов перегретым паром в системе Mathcad 15.

Поверхности, отражающие изменение температуры Т , K, и влагосодержания и , кг/кг, по ходу процесса т , мин, и по слоям продукта, представлены на рисунках 2 и 3.

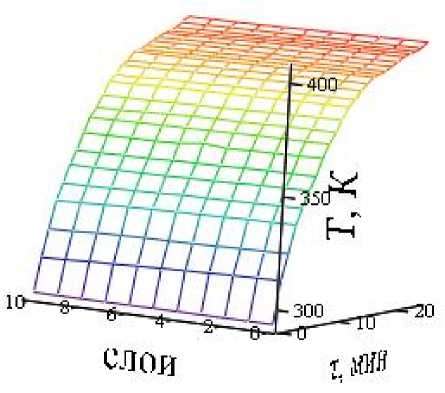
Рисунок 2 - Поверхность изменения температуры по ходу процесса и по слоям продукта

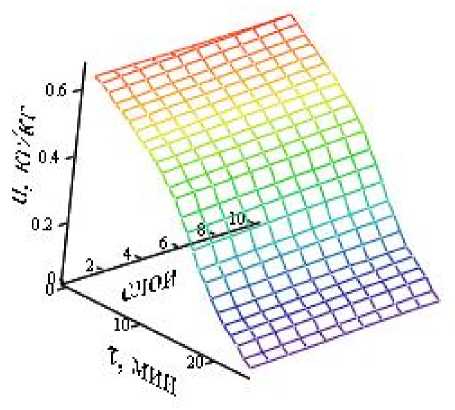
Рисунок 3 - Поверхность изменения влагосодержа-ния по ходу процесса и по слоям продукта

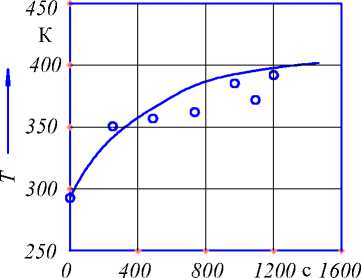
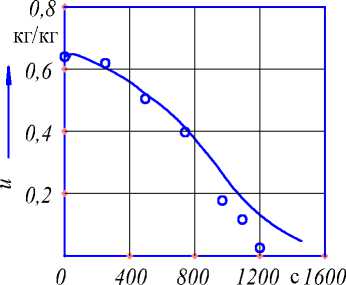
По сравнительному анализу результа-тов аппроксимации расчетных и экспериментальных данных (рисунки 4, 5) установлено, что их отклонение по абсолютному значению не превышало для температуры 3,5 % и для влагосодержания 11,0 %.

τ

Рисунок 4 - Термограмма тепломассопереноса при обжарке каштанов: сравнение расчетных () и экспериментальных (о) данных при обжарке перегретым паром, Т_п = 473 K; q_H = 9,8 кг/м ² ; v = 1,3 м/с

τ

Рисунок 5 - Кривая обжарки каштанов: сравнение расчетных () и экспериментальных (о) данных при обжарке перегретым паром, Т_п = 473 K; q_H = 9,8 кг/м ² ; v = 1,3 м/с

Таким образом, полученные результаты моделирования с достаточной для инжен ерных расчетов точностью отражают кинетические закономерности процесса обжарки каштанов перегретым паром как объекта с распределенными параметрами и могут быть использованы для анализа протекающих физикохимических изменений, расчета процесса, проектирования обжарочных аппаратов и разработки программно-логических алгоритмов управления технологическими параметрами.