Математическая модель связи гидрохимических показателей качества воды водоема-охладителя БГРЭС-1

Введение . Основой научного подхода к управлению качеством воды водного объекта является математический анализ зависимости процессов изменения качества воды, поступающей на выход из водоема, от качества воды на входе в водоем-охладитель. Характерная особенность процессов формирования качества воды в водоеме-охладителе БГРЭС-1 - их зависимость от большого числа управляемых и неуправляемых факторов (температура, время, морфология водоема, гидрометеорологические условия, содержание ингредиентов в речном стоке и т. п.) [1], многие из которых изменяются стохастически. Проведено математическое моделирование связей между параметрами качества воды стока и поступления аллохтонных, автохтонных биогенных веществ при антропогенных нагрузках и проанализировано их влияние на экосистему водоема-охладителя. Произведена количественная оценка вклада в изменение параметров качества воды притока рек, теплового сброса электростанции, поступлений органических и биогенных веществ из затопленных почв, торфа в процессе формирования качества воды водоема-охладителя за длительный период времени, что создает научную базу для прогноза экологического состояния водоемов-охладителей атомных и тепловых электростанций.

При моделировании должны учитываться такие факторы, как массо- и теплоперенос, гидродинамика, кинетика множества одновременно протекающих процессов, которые почти не поддаются разграничению в натурных условиях. Они характеризуют процессы формирования качества воды как диффузные, плохо организованные системы [2, 3]. Задачи исследования и оптимизации таких систем успешно решаются с использованием идей и методов многомерной математической статистики. При этом существенно меняются представления о математическом описании явлений: понятие «физический закон» заменяется более широким понятием «математическая модель». Одну и ту же систему можно описывать различными моделями, специально оговаривая степень адекватности описания и те критерии, которые привлекаются для оценки адекватности.

Цель исследования : с помощью математической модели связи гидрохимических показателей качества воды в стоке из водоема и его верхней части дать прогноз экологического состояния водоема.

Методы исследования. Основные химические превращения компонентов водной среды при формировании гидрохимического режима в принципе могут быть адекватно описаны системой дифференциальных уравнений, составленных на основе законов химической кинетики и термодинамики. Эти уравнения позволяют прогнозировать динамику превращения компонентов воды в широком диапазоне изменения переменных факторов (температуры, концентраций растворенных веществ) в водоеме, но для их получения требуется глубокий теоретический анализ протекающих процессов, создание уни- кальных компьютерных программ, большой объем вычислений.

Для решения оптимизационных задач более пригодны полиноминальные уравнения. При описании плохо организованных систем процессы фигурируют в виде «черного ящика» [3], а зависимости между входными и выходными параметрами представляются в виде уравнений регрессии. Коэффициенты регрессии интерпретируют как коэффициенты ряда Тейлора. Уравнения дают возможность с определенной точностью прогнозировать значения выходных параметров в области изученного факторного пространства, их можно использовать для оптимизации процессов. К достоинствам метода относится исключительная универсальность, возможность применять однотипные алгоритмы для моделирования и оптимизации разнообразных процессов [4].

Результаты исследований . Водоем-охладитель Березовской ГРЭС-1 сооружен в 1986 г. зарегулированием стока реки Береш в районе впадения в нее рек Базыр и Кадат. Мониторинг качества воды осуществляли отбором и анализом проб воды в течение десяти лет – с 1987 по 1996 г., с периодичностью 2 месяца (6 наблюдений в год); объем выборки составил 58 проб. На рисунке 1 представлена схема акватории водоема-охладителя, расположение и номера точек отбора проб.

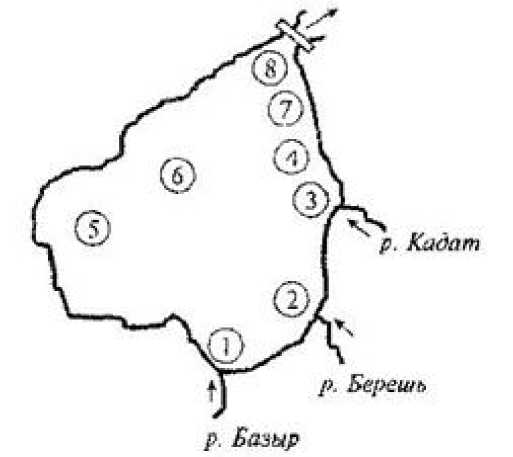
Рис. 1. Схема акватории водоема-охладителя и расположения точек отбора проб воды

Контрольные точки 1, 2 и 3 расставлены в устьях рек. По результатам анализов проб воды в этих точках можно судить о составе и количестве загрязняющих веществ, поступающих в водоем с речным стоком. Точка 4 расположена в устье сбросного канала теплоэлектростанции, точка 5 – в левобережье, в районе торфяного месторождения. Пробы в точке 6 характеризуют качество воды в самой глубоководной центральной части водоема. Здесь происходит усреднение свойств воды, поступающей из рек. В точке 7 контролируется качество воды в районе водозаборного канала электростанции. Пробы в точке 8 характеризуют качество воды в приплотинной части водохранилища; здесь происходит аккумуляция всех загрязнений, как аллохтонного, так и автохтонного происхождения.

В таблице 1 приведены характеристики выборки: контролируемые показатели, их минимальные ( Х min ) и максимальные ( Х max ) величины.

Таблица 1

Показатель	Обозначения показателей	Размах варьирования
		Х min	Х max
Температура, оС	Х 1	0,1	29,5
Перманганатная окисляемость, мг/дм3	Х 2	5,3	110,2
Цветность, градусы цветности	Х 3	0	240
Концентрация кислорода, мг/дм3	Х 4	1,2	18,1
Концентрация ионов аммония, мг/дм3	Х 5	0,05	6,54
Концентрация фосфат-ионов, мг/дм3	Х 6	0,01	0,75

Характеристика выборки показателей качества воды Х i

Математический анализ результатов наблюдений дает возможность установить характер изменения качества воды стока из водоема-охладителя (в приплотинном участке, точка отбора проб 8). Состав воды в значительной степени зависит от поступлений химических ингредиентов с речным стоком, а ряд других параметров, таких как температура, цветность, концентрация растворенного кислорода, – от теплового сброса электростанции и автохтонных процессов. Количественную оценку этих зависимостей произвели методом математического моделирования. В соответствии с задачами и программой исследования, в качестве независимых переменных (факторов) использовали характеристики воды Х 1 ... Х 6 , перечисленные в таблице 1, в точках отбора проб 1–7, а в качестве выходных параметров (откликов) – те же характеристики в точке 8.

Зависимости выходных параметров от переменных факторов аппроксимировали линейными уравнениями регрессии общего вида:

Х i ,8 = b 0, j + Σ b i,j X i,j , (1)

где первые подстрочные индексы i = 1, ..., 6 – номера факторов (см. табл. 1); вторые подстрочные индексы j = 1, ..., 8 – номера точек отбора проб (см. рис. 1). Численные значения свободных членов b 0, j и коэффициентов регрессии b i,j определили методом наименьших квадратов, статистическую значимость членов регрессии – методом дисперсионного анализа (пакет прикладных программ Statgraphics Plus for Windows V.5) [4]. Незначимые члены (при критическом уровне значимости 5 %) исключили из уравнений с пересчетом коэффициентов регрессии в оставшихся членах. Результаты вычислений приведены в таблице 2. Все члены с коэффициентами b i, 6 и b i, 7 оказались незначимыми, они не включены в таблицу 2. В последней строке таблицы 2 – дисперсионные отношения Фишера F эф , служащие для оценки эффективности моделей. Обычно полагают (хотя это формально не обосновано), что модели представляют практическую ценность, если F эф > 2. В обсуждаемом исследовании все математические модели продемонстрировали высокую эффективность.

Таблица 2

Статистически значимые коэффициенты регрессии и эффективности математических моделей

Коэффициент	Показатель
	Х 1	Х 2	Х 3	Х 4	Х 5	Х 6
b ..., 0	0,955	2,434	26,112	-4,398	0,101	0,020
b ..., 1	–	–	–	1,160	–	–
b ..., 2	0,438	0,315	–	-1,038	–	–
b ..., 3	0,282	–	–	0,966	0,040	0,369
b ..., 4	0,039	–	–	–	–	–
b ..., 5	0,198	0,268	0,225	0,604	0,604	0,211
F эф	12	46	38	18	32	13

Таким образом, уравнения регрессии (1) приобретают конкретный вид:

Х 1,8 = 0,955 + 0,438 X 1,2 + 0,282 X 1,3 +

+0,039 X1,4+ +0,198 X1,5;(2)

X2,8 = 2,434 + 0,315 X2,2 + 0,268 X2,5;(3)

X3,8 = 26,112 + 0,225 X3,5;(4)

X4,8 = –4,398 + 1,160 X4,1 – 1,038 X4,2 + +0,966 X4,3 + 0,604 X4,5;(5)

X5,8= 0,101 + 0,040 X5,3+ 0,604 X5,5;(6)

X6,8= 0,020 + 0,369 X6,3+ 0,211 X6,5.

Наглядное представление о качестве моделирования дают графики сопоставления наблюдавшихся натурных измерений и вычисленных по моделям значений выходных параметров. На рисунке 2 приведен один из таких графиков – температура Х 1,8 . Большинство измеренных значений расположено вблизи диагональной прямой (геометрическое место вычисленных значений температуры), в 95 %-м доверительном интервале, обозначенном пунктирными линиями с обеих сторон прямой. Мы не приводим здесь графики для пяти других выходных параметров, так как они имеют аналогичный вид. Результаты моделирования можно считать успешными, учитывая высокий уровень «зашумленности» на природном объекте.

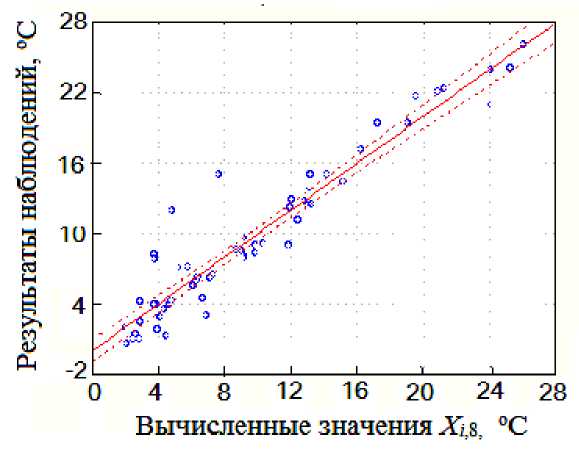
Рис. 2. Расчетные и экспериментальные значения температуры

В уравнениях регрессии присутствуют только члены первого порядка, что позволяет обсудить основные закономерности формирования качества воды в приплотинной части непосредственно по величинам коэффициентов регрессии.

Температура воды на выходе из водоема-охладителя Х 1,8 существенно зависит от температуры воды речного стока р. Береш: величина коэффициента b 1,2 в уравнении (1) – самая большая. Коэффициент b 1 , 3 , характеризующий степень влияния стока р. Кадат, по величине примерно в полтора раза меньше. Коэффициент b 1,6 , показывающий вклад температуры воды в центральной части водоема в формирование температуры на выходе, вдвое меньше, чем вклад стока р. Береш. Величина коэффициента b 1 , 4, отражающего вклад температуры воды в устье сбросного канала, на порядок меньше, чем влияние стоков рек Береш и Кадат. Проведенными ранее натурными исследованиями [5] установлено, что тепловой сброс электростанции непосредственно не повышает температуру воды в приплотинной части водоема. Все члены уравнения имеют положительные знаки, т. е. увеличение температуры в исходных точках приводит к повышению температуры на выходе из водоема.

Показатель перманганатной окисляемости Х 2,8 характеризует содержание растворенного органического вещества на выходе из водоема. Наибольшее влияние на него оказывает качество воды в устье р. Береш и в районе основного торфяника (точки контроля 2 и 5). Река Бе-реш имеет самый большой объем стока, который вносит существенный вклад в суммарное содержание растворенного органического вещества. Немного меньшее влияние оказывает растворенное органическое вещество, которое продуцируется торфяником. Действия этих факторов направлены в сторону увеличения показателя окисляемости.

Величина показателя цветности воды на выходе из водоема Х 3,8 обусловлена только процессами разложения основного торфяного месторождения и растворением окрашенных составляющих торфа – фульвокислот и гуминовых соединений.

Трансформация растворенного в воде кислорода имеет сложный характер. Его запасы пополняются за счет растворения атмосферного кислорода и снижаются из-за расходования на окисление содержащихся в воде органических веществ. Кроме того, этот фактор наиболее подвержен сезонным колебаниям. Детальное обсуждение всех нюансов выходит за рамки настоящего сообщения, оно имеется в публикации [1].

Содержание аммонийного азота на выходе из водоема Х 5,8 зависит, главным образом, от интенсивности его образования при разложении торфа, в значительно меньшей степени – от поступления со стоком р. Кадат.

Показатель концентрации фосфат-ионов Х 6,8 формируется за счет поступлений из затопленного торфяника (точка отбора проб 5) и заторфо-ванного устья р. Кадат (точка 3), а также за счет антропогенного загрязнения стока этой реки.

Выводы

• 1.    Между свойствами воды в характерных областях акватории водоема-охладителя тепловой электростанции, с одной стороны, и в приплотинной области стока, с другой стороны, существуют      аддитивные      причинно

• 2.    Математическое моделирование может служить методологической основой оптимизации качества воды водоемов-охладителей ТЭС для технологических целей и аквакультуры.

следственные зависимости, поддающиеся математическому моделированию методами регрессионного анализа.