Математическая модель течения расплава в канале гранулятора

DOI:

Введение. В процессе гранулирования углеводно-витаминно-минеральных добавок (УВМД) на основе мелассы качество гранул определяется давлением и температурой расплава, которые зависят от соотношения площади и размеров кольцевого канала [1]. В связи с тем, что обработка углеводно-витаминно-минеральных добавок (УВМД) на основе мелассы в грануляторе проводится при более высокой влажности (до 26 %), а разогрев продукта осуществляется за счет эффекта диссипации, то для стабильной работы гранулятора необходимо обеспечить создание достаточного давления в матричной зоне.

Материалы и методы исследований. Для описания неизотермического течения расплава в грануляторе используем следующие уравнения [3]:

• уравнение неразрывности:

др др др др     ( д v_x  ^д v    дv_z I

+ vx   +     + vz= -р| —+ + —y + дт   x дx   y дy   z дz     (дx   дy   дz ), ()

Система уравнений (1–5) не может быть решена в общем виде [1, 3, 5]. Поэтому для расчета полей скоростей и температур в грануляторе были приняты следующие допущения: течение расплава в грануляторе представляет собой установившийся (профиль скоростей потока не изменяется с течением времени) ламинарный (числа Рейнольдса Re = 2rvzP /n ” 2100) поток; по сравнению с силами трения и давления силами инерции и гравитации можно пренебречь; расплавы представляют собой несжимаемые жидкости; градиент скорости в направлении течения значительно меньше, чем в поперечном направлении; градиент давления по поперечному сечению канала постоянен; в каждом поперечном сечении канала течение является полностью гидродинамически развитым; влиянием эффектов на входе в канал и выходе из него можно пренебречь [4].

В связи с принятыми допущениями [5] уравнение неразрывности (1) принимает вид:

где v x , v y и v z – компоненты вектора скорости;

• уравнение движения:

d v d T	_ д р д x	( дт --л^ + ( д x	д т yx + д y	дт zx		+ р g x
				д z	7
dv 5 y	д р	( 6т xy	дт yy .	дт хХ	।	+ р§у
р—	=--	--+	+
d T	д y	( д x	д y	д z	7	y
dvz	д р	( дт^ +	дт yz	дт zz	I
р—-	=--		—— +			+ р§2
d T	д z	( д x	д y	д z	7	z

, (2)

+    ⁽ P ^Vx ) +    ⁽ P ^Vy ) + ⁽ P ^Vz ) = ⁰, ⁽⁸⁾

д t дx       дy       дz а после всех упрощений:

д /    \ n -   д v_x

(р^) = о = р—x дx            дx

др v x , д x

* V ^

=0 т . к . р = const

д v а р^ = ⁰, д x

Из уравнения (9) следует, что, поэтому:

здесь g – вектор ускорения свободного падения;

•реологическое уравнение:

д v_x а

—- = 0 д x

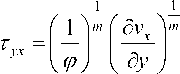
Если в процессе неизотермического течения наблюдается теплопередача, то для описания такого процесса необходимо включить следующие уравнения:

• уравнение энергии:

р— \ U +—v2 | = -Vq + р(vg) - dT (    2 J           ' '             (4)

- V p v - V ( t v )

здесь q - вектор потока теплоты (с компонен тами qx, qу, qz), a 2222; а диссипаци-xyz онный член равен:

„ -     dv,     dvy     dvz     ( дv дvyI xyzxy xx 7         yy    7 zz    7         xy II dx       dy       dz      l дy   дx)

,     \            x      ⁷ , (5)

( д vy   д v  |     ( д v   д

+ Tyz I      +      I + т„ I+ I y ( дz дy 7    ( дx дz 7

Комбинируя упрощенное уравнение неразрывности (10) с упрощенным уравнением

движения, получаем:

® p P^^ yx = 0

д x    д y

Уравнение энергии (4):

^{р с} _Р

< д T     д T      д T      д T )

\ — + v — + + v — + + v -- =

( д t     ^x д x      ^y д y      ^z д z 7

_ ( ^д C x ,^д q , ,^д C z I

= --11--

( д x д y    д z 7

( dpA ( д v ^д v, д v I

- T\ -P I      +    + z-

( д T 7 _р ( д x д y д z J

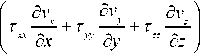
т

( д v   д v I xyP +

( д y   д x 7

+ т

xz

( д v д v | I + z " I ( д z д x 7

( д v y д v I

\    ⁺ ~Pz

( д z д y 7

,(12)

После упрощения уравнения (12) принимает вид:

—

^- q .

^^^^^^е

д у

dv дт -x- = о , xy - z

Уравнения (11)-(13) образуют замкнутую систему нелинейных дифференциальных уравнений в частных производных.

T напряжение сдвига x принимает нулевое значе- r = £R ние при        (рисунок 1), где скорость vz при нимает максимальное значение (vz)max.

Внешний радиус кольцевого зазора равен R. Таким образом:

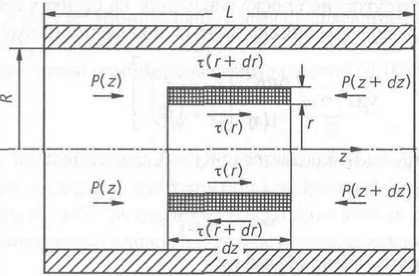
Рисунок 1. Равновесие сил, действующих на массовый элемент потока в канале круглого поперечного сечения

C =

4² A pR¹

2 L

Подставляя (19) в уравнение (18), получаем:

A pR

^{T r} ) = -LT

r 2R r " 4 7

Скорость сдвига для течения расплава в грануляторе рассчитывается по формуле:

d k = _— A pR r_ _— 4 R dr    2 p L L R r

Далее рассмотрим течение расплава в канале круглого поперечного сечения (с радиусом R и длиной l ), в котором влиянием эффектов на входе и выходе пренебрегаем. При этом считаем, что в выделенном элементе (рисунок 1) с толщиной слоя dr , движущегося со скоростью v_z , устанавливается равновесие сил [3]:

Интегрируя уравнение (21), получаем:

^- _z ^{( r} ) =

A pR 2 p L

— 2 4 In | R | + C 2

I r )

2 n rdr • [ p ( z ) — p ( z + dz )] + t • 2 n rdz —

— t ( r + dr ) • 2 n • ( r + dr ) • dz = 0

. (14)

Разложив выражение (14) в ряд Тейлора и отбросив все члены, кроме первого, вследствие их малости, получаем [3]:

- p p ( z + dz ) = p ( z ) +— dz

- z

-T , t ( r + dr ) = t ( r ) +— dr - r

Значения двух неизвестных величин ⁴ и С 2 можно определить, используя следующие граничные условия:

• при r = kR , v z = 0,

• при r = R, vz =0, здесь k = Ri /R - соотношение внутреннего и внешнего радиусов кольцевого зазора.

Тогда постоянная интегрирования:

С 2 =–1.             (23)

Подставив граничные условия и (23) в уравнение (22), получаем:

Поскольку течение является полностью развившимся, градиент давления можно считать постоянным:

к ² — 1

2ln k ,

- p _ A p

- z   L

Результаты исследований. Таким образом, распределение скоростей можно выразить следующей формулой:

Отбросив все члены высшего порядка, получаем следующее дифференциальное уравнение:

A p t d T 1 -

= ~ + ^T = ~ T^' r ).     (17)

L r dr r - r

^V z ⁽ r ) =

R ² A p 4 p L

r

^^^^^^»

R

+ 2

2ln k

— k2

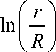
В результате интегрирования уравнения (17) получаем уравнение движения для течения

r = 4 R

Когда , получаем выражение для максимальной скорости потока ( v 2 ) max :

расплава в канале круглого сечения:

( ^Vz )

^z max

T r ) = C ^r + CL,           (18)

2 Lr

R² A p 1 1 _— к ² — 1 4 n L I 2ln к

1 — In

к — 1 I ч 2ln к )

Средняя скорость рассчитывается по

Чтобы решить уравнение (14) для данного случая, необходимо сделать предположение, что

уравнению:

— R ² A p 1 — к ⁴   к ² — 1

V =---- ---т-- z 4pL 1 — к2 2ln к

Вестник ВГУИТ, №1, 201 6

Умножая выражение для средней скорости на площадь поперечного сечения кольцевого зазора, получаем уравнение для определения объемного расхода Q :

Q = nR ²(1 - k ²) ■ V_z =

= 1 1 4 [ (1 — k ⁴) — 0,7( k 2 — 1) 3/2 ln k ] A p ^ . ⁽²8)

Среднее время пребывания расплава в канале обратно пропорционально средней скорости:

Проведен сравнительный анализ характера течения реологического раствора при различных значениях индекса течения n = 1, 3, 5 (рисунок 3).

Установлено, что средняя скорость течения расплава вдоль оси убывает на участке до 2/3 длины канала, а затем возрастает.

Результаты расчетов по полученным уравнениям хорошо согласуются с экспериментальными данными, отклонения изменялись в диапазоне 16–19 %.

t ® LI V z

8 n L

R ² A p

1 - k⁴

1 - k^г

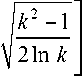
Были также получены:

– уравнение для определения напряжения сдвига τ:

Ap т=-L- • x;                  (30)

– уравнение для определения скорости сдвига γ:

2( m + 2) ■ Q n DH²

– уравнение для определения потери дав-

( A p I L )

ления ^p :

A p = 12 p Q L    n DH³ "

Уравнения (30), (31) и (32) были получены на основе вышеприведенных допущений и упрощений.

Обсуждение результатов. Исходные данные для выполнения расчетов приведены в таблице 1.

Т а б л и ц а 1

Исходные данные для расчета скорости течения расплава

Наименование параметра	Обозначение	Значение
Плотность расплава, кг/м3	р	1190
Динамическая вязкость, Па∙с	п	12800
Индекс течения	n	1, 2, 3
Объемный расход, м3/c	Q 0	0,543∙10-5
Угловая скорость, с-1	to	8,5
Радиус матрицы на входе, м	R n 2	6,0∙10–3
Радиус матрицы на выходе, м	R k 2	12,5∙10–3
Длина матрицы, м	L	20,0∙10–3
Число узлов сетки	K	11

Расчет осевой скорости так же проводился для N участков, результаты расчетов приведены на рисунке 2.

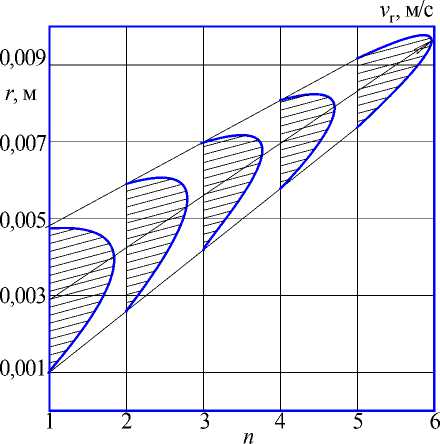
Рисунок 2. Распределение осевых скоростей течения расплава в цилиндрическом зазоре гранулятора на его разных участках аппроксимации

Полученные сведения о характере перемещения расплава в грануляторе позволили разработать методику расчета для проектирования рациональной конструкции формующего

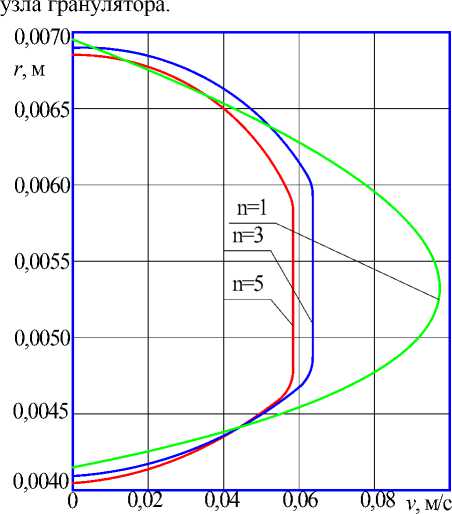
Рисунок 3. Распределение осевых скоростей течения расплава в цилиндрическом зазоре гранулятора при различных индексах течения на одном из участков