Математическая модель тепло- и массопереноса при вакуумной сушке арахиса с комбинированным теплоподводом

Арахис является ценным сырьем для пищевой промышленности. От выбора способа сушки и режимных параметров этого термолабильного материала существенно зависят интенсивность сушки, исключающая потери материала из-за его порчи, способность высушенного материала к длительному хранению, а также его качественные показатели [1–5]. Использование «мягких» температурных режимов положительно сказывается на качестве материала при его последующей обжарке. Это и определило выбор вакуумного способа сушки с комбинированным теплоподводом, в полной мере отвечающего всем перечисленным требованиям [6–10].

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License

Материалы и методы

Считаем, что процесс протекает в сушильной камере, содержащей пар удаляемой жидкости и незначительное количество посторонних газов (в том числе воздуха), которые непрерывно удаляются из камеры так, что в ней поддерживается постоянное давление p ≈ p = const .

Камера снабжена нагревателями, их температура T является управляемым параметром. Передача теплоты от нагревателей к материалу может быть кондуктивной, конвективной, радиационной или совокупной. В последнем случае теплота передается всеми тремя способами одновременно, то есть имеет место сложный теплообмен.

Составим математическое описание обоих периодов сушки: периода поверхностного испарения (1-го периода сушки) и периода внутреннего испарения (2-го периода сушки) при комбинированном теплоподводе.

Результаты

Период поверхностного испарения (1-й период сушки). В этом периоде испарение влаги локализовано на поверхности материала и скорость ее испарения определяется интенсивностью внутреннего и внешнего подвода теплоты к поверхности испарения. Поэтому уравнение кинетики сушки имеет вид:

du_x ( т ) / d T = - ( rM ) ^{- 1} x

x [ kF (T 1 ( T ) - T_s ) + k a F m (T c - T s ) ] ,    ⁽¹⁾

Температуру насыщенного пара (она равна температуре поверхности продукта) принимаем T = const . В уравнении (1) и далее по тексту индексы 1 и 2 у переменных и ( т ) и T (т ) относят его к 1-му и 2-му периодам сушки.

Уравнение теплового баланса:

kaF (Tc - Ts) = м(С + cвU1 (т)) x xdT (т) / dт - rMdu1 (т) / dт.

где левая часть представляет тепловой поток от нагревателей к поверхности материала, а первый и второй члены правой части – тепловые потоки, направленные, соответственно на изменение средней температуры материала и на испарение влаги. Коэффициент теплопередачи k учитывает различные виды внешнего теплообмена – контактную теплопроводность, конвекцию и излучение (в линейном приближении), а коэффициент k представляет механизм внутреннего теплопере-носа путем обычной теплопроводности и перемещения влаги в порах (капиллярах). Оба эти коэффициента условно приведены к общей поверхности теплопередачи F .

Известно, что значения удельной теплоемкости различных материалов и удельной теплоты испарения в зависимости от температуры изменяются в довольно узком диапазоне. Поэтому в дальнейшем считаем, что величины c, cB, r не зависят от температуры в пределах ее изменения в данном процессе. Кроме того, принимаем приближенно смн = c + cBUi ~ с + си ■         (3)

мн           в 1           в н

Такое допущение оправдано, поскольку производная dT (т)/ d т существенна лишь в начальной стадии первого периода, когда величина и (т ) незначительно отличается от начального влагосодержания материала u . В этом случае система уравнений (1), (2) становится линейной.

Введя безразмерные комплексы K_r, К^, K_a и перейдя к безразмерным переменным t = T / T , t_c = T / T_s и F = Кт , получим решение системы (1), (2):

U 1 F ) = U н + K _a K-_r' o - к;\ t н - 1) x

^θ               (4)

• ^x [ 1 ^- e^XP^{( -} K ^{F )} ] ^{- K} a ^K r J t с ^{( F -} n ) d n ;

t 1 F) = 1 + ( t н - 1)exp( - K F).      (5)

• ^U 1⁽⁰⁾ = ^U н

• t 1 (0) = t н .

Безразмерный комплекс t_H = T / T , где T – начальная температура материала.

В частном случае, при t = const из (4) следует:

U 1 F ) = U н + K a K;^l(t с - 1) F -

• - к - ( t н - 1) [ 1 - exp( - K F ) ] ;

Период внутреннего испарения (2-й период сушки). Существенным признаком рассматриваемого периода является рассредоточение зоны испарения влаги по объему материала. Основным фактором, лимитирующим скорость сушки в этом периоде, является скорость внутреннего влагопереноса, и уравнение кинетики сушки имеет вид:

dU ( т )/ d т = - К ( u₂ ( т ) - u ),     (7)

Равновесное влагосодержание u зависит от давления пара и температуры материала, но при достаточно низком остаточном давлении оно практически близко к нулю. Тогда du, (т)/ dт = - К • и2 (т)         (8)

Уравнение теплового баланса запишем в виде:

k т F т ( T c - T ₂ ( т )) = M [ c + c в и ₂ ( т ) ] dT ₂ ( т )/ d т -

• - M [ r + c _n ( T ( т ) - T_s ) ] du₂ ( т )/ d т

Левая часть уравнения (9) представляет тепловой поток от нагревателей в объем материала, а второй член правой части – суммарный поток, идущий на испарение и перегрев пара. Коэффициент k учитывает как внешние, так и внутренние механизмы переноса теплоты.

Обычно величина c ( Т ₂( т ) - T_s ) , входящая в уравнение (9), мала по сравнению с r , и ею можно пренебречь. Кроме того, будем считать, что величины с , с_в, r не зависят от температуры в пределах ее изменения в данном процессе.

Разделив левую и правую часть уравнения (9) на M и объединив его с (8) получим систему уравнений:

к т f. ( T_c - T i d )) = ( c + С в и 2 ( т )) *

х dT ( т )/ d т - r x du₂ ( т )/ d r ;

du ₂( т )/ d r = - K x и ₂( т ); ⁽¹⁰⁾ и ₂( т ’) = и ₁( т ’) = и ’;

Т2(т ’) = Т(т’) = T \ где т* - момент времени, соответствующий переходу от режима поверхностного испарения в режим внутреннего испарения, с; и * - «критическое» влагосодержание материала, кг влаги/кг сухого материала; Т * - температура материала в конце 1-го периода сушки, K.

Уравнение (8) является дифференциальным уравнением с разделяющимися переменными. Результатом его решения является:

и ₂ ( т ) = и * exp( - К т ). (11)

Подставив (8) и (11) в уравнение (10) получим:

kтf: (тс - T2(т)) =(С + Св •и * exP(-Кт)) х хdT (т) / dт + r • К • и * exp(-Кт)

Тогда dT (т)/ ат =

₌ к _т f с (T — T 2 ( т )) - r • К • и *• exp( - К т ) .

c + c _в • и * • exp( - Кт)         ’(12)

*

и ₂ ( т ) = и ( т ) = и ;

T ( т *) = Т ( т *) = Т *.

В случае отсутствия 1-го периода сушки, начальными условиями будут и 2(0) = ин;                (13)

T 2 (0) = Т н .                (14)

Уравнение (12) является линейным дифференциальным уравнением 1-го порядка, решение которого можно найти методом Бернули или методом вариации произвольной постоянной. Однако при решении возникают интегралы, которые нельзя вычислить на классе элементарных функций. Поэтому были проведены вычислительные эксперименты в среде редактора MathCAD и получены решения уравнений (11) и (12) в виде графических зависимостей и (т ) и Т(т ) с известными начальными условиями и ( т ) и Т ( т ₀) . Поведение переменных параметров материала во 2-м периоде показано на рисунках 1–5.

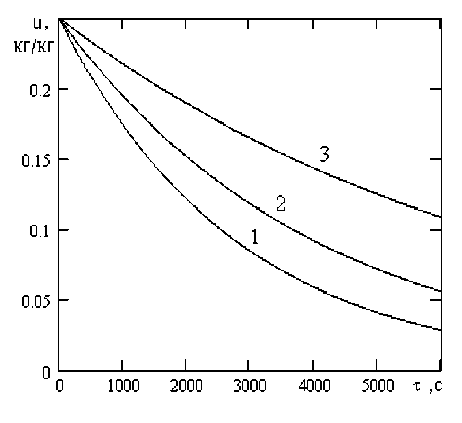
Рисунок 1. Расчетные кривые сушки арахиса при p = 9,8 кПа, Т с = 323 K, k т = 60 Вт/(м² K), f t = 0.16 м²/кг для различных значений коэффициента сушки K, ч^-1: 1 – 1,3; 2 – 0,9; 3 – 0,5

Figure 1. Calculated drying curves for peanuts at p = 9.8 kPa, T c = 323 K, k т = 60 W/(m²·K), f t = 0.16 m²/kg for various values of the drying coefficient K, h⁻¹: 1 – 1.3; 2 – 0.9; 3 – 0.5

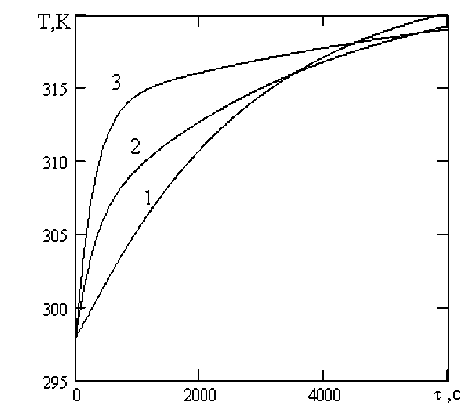
Рисунок 2. Расчетные температурные кривые процесса вакуумной сушки арахиса при p = 9,8 кПа, Т с = 323 K, k т = 60 Вт/(м² K), f t = 0.16 м²/кг для различных значений коэффициента сушки K, ч^-1: 1 – 1,3; 2 – 0,9; 3 – 0,5

Figure 2. Calculated temperature curves of the vacuum drying process for peanuts at p = 9.8 kPa, T c = 323 K, k т = 60 W/(m²·K), f t = 0.16 m²/kg for various values of the drying coefficient K, h⁻¹: 1 – 1.3; 2 – 0.9; 3 – 0.5

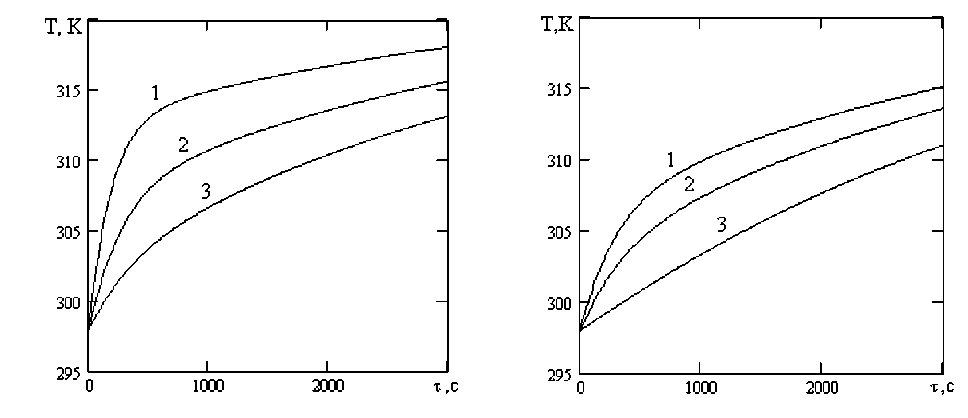
Рисунок 4. Расчетные температурные кривые процесса вакуумной сушки арахиса при p = 9,8 кПа, К = 0,87 ч^-1, Т с =323 К, f t = 0,16 м²/кг для различных значений коэффициента теплопередачи k т , Вт/(м² К): 1 – 60; 2 – 50; 3 – 40

Рисунок 3. Расчетные температурные кривые процесса вакуумной сушки арахиса при p = 9,8 кПа, K = 0,87 ч^-1, Т с =323 К, k т = 60 Вт/(м² К) для различных значений удельной поверхности теплопередачи f t , м²/кг: 1 – 0,25; 2 – 0,17; 3 – 0,13

Figure 3. Calculated temperature curves of the vacuum drying process for peanuts at p = 9.8 kPa, K = 0.87 h⁻¹, T c = 323 K, k т = 60 W/(m²·K) for various values of the specific heat transfer surface area f t , m²/kg: 1 – 0.25; 2 – 0.17; 3 – 0.13

Figure 4. Calculated temperature curves of the vacuum drying process for peanuts at p = 9.8 kPa, K = 0.87 h⁻¹, T c = 323 K, f t = 0.16 m²/kg for various values of the heat transfer coefficient k т , W/(m²·K): 1 – 60; 2 – 50; 3 – 40

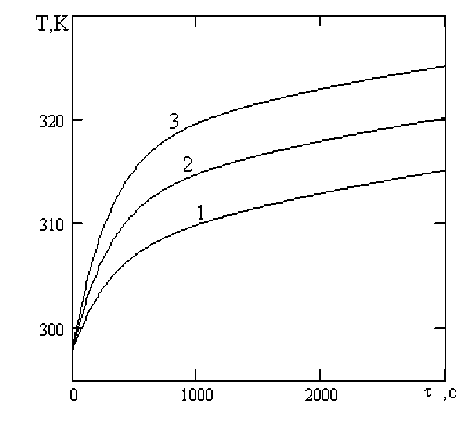
Рисунок 5. Расчетные температурные кривые процесса сушки арахиса при p = 9,8 кПа, K = 0,87 ч^-1, f t = 0,16 м²/кг, k т = 60 Вт/(м² К) для различных значений температуры нагревателя Т с , K: 1 – 323; 2 – 328; 3 – 333

Figure 5. Calculated temperature curves of the drying process for peanuts at p = 9.8 kPa, K = 0.87 h⁻¹, f t = 0.16 m²/kg, k т = 60 W/(m²·K) for various values of the heater temperature T c , K: 1 – 323; 2 – 328; 3 – 333

остаются качество продукта и продолжительность сушки. Первый из них обычно задают в виде ограничения на температуру материала (в некоторых случаях во избежание растрескивания и коробления материала ограничивают также градиенты температуры и влагосодержа-ния). Поскольку с повышением температуры материала скорость влагоудаления всегда возрастает, задача оптимизации сводится к управлению теплоподводом так, чтобы материал максимально быстро нагрелся до допустимой температуры, а далее его температура оставалась постоянной. Максимально быстрый нагрев материала можно обеспечить, максимально увеличив температуру нагревателя T в начале процесса. В этом случае T ограничена только допустимым градиентом температуры для данного материала. В ходе дальнейшего процесса температура материала должна оставаться постоянной и равной максимально допустимой для данного продукта, т. е.

T ( t ) = var;

.

T _x = T _m ax = const ci     max

T ₂ ( т ) = T_g = const ; T_c2 ( t ) = var .     (16)

Влагосодержание арахиса (рисунок 1) уменьшается с падающей скоростью, стремясь к равновесному значению, причем тем значительнее, чем выше значение коэффициента сушки K . Скорость повышения температуры арахиса в начале процесса (рисунок 2) напротив ниже при больших значениях коэффициента сушки, поскольку значительная часть передаваемой теплоты расходуется на испарение влаги из материала, а не на повышение его температуры. Однако по истечении определенного времени отмечается более интенсивное повышение температуры материала при более высоких значениях K . Температура материала повышается тем быстрее, чем больше значения удельной поверхности теплопередачи f (рисунок 3), коэффициента теплопередачи k (рисунок 4) и температуры нагревателя T (рисунок 5).

Оптимальное управление процессом вакуумной сушки. Основные критерии оптимизации сушильных процессов, мало зависящие от изменчивой конъюнктуры и сравнительно просто поддающиеся количественной оценке, таковы (в приоритетном порядке): качество получаемого продукта, удельные энергозатраты (на единицу массы испаренной влаги) и продолжительность сушки. При вакуумной сушке удельные энергозатраты слабо зависят от интенсивности процесса, поэтому главными критериями

Хотя T может изменяться при переходе от одного к другому режиму сушки, далее для простоты считаем ее постоянной. Следовательно, задача оптимизации процесса состоит в определении такой функции Tc (т) , которая обеспечивала бы выполнение условий (15), (16).

Будем считать, что процесс с самого начала вступает в стадию внутреннего испарения.

Для начального этапа уравнения (11), (12) запишутся в виде:

щ (т ) = u _H exp( - K t ) .

dT ( т )/ d r =

₌ k т f : ^{( T} max — ^{T ( t} )) — r ' ^K ' u н ' e^XP⁽ — ^{K t} ) ; c + c_B • u_H • exp( - K t )

После достижения температуры материала T ( t ) = T , что соответствует моменту времени т^ начинает выполняться условие dT₂ (т ) / d T = 0 . Найдем функцию Т ₂ ( т ) которая обеспечит выполнение условия dT ₂ ( т ) / d T = 0 .

k т f _? ( T c2 ( T ) - Т д ) - r • К • u н • exp( - K t ) _=q

c + c_B • u_H • exp( - K t )

Тогда:

^T c2 ^{( T} ) = T ⁺ r • ^К • u н • ^exp⁽ — ^{K T} ) / ^k т ^f т (18)

Практическая реализация оптимального теплового режима сушки путем непрерывного изменения температуры нагревателей в соответствии с формулой (18) требует специальной системы программного управления. Техническое решение этой задачи упрощается при ступенчатом изменении температуры нагревателей. Особенно просто такой режим теплоподвода осуществляется в аппаратах непрерывного действия, где по ходу перемещения материала устанавливаются нагреватели разной мощности.

В качестве примера проиллюстрируем кинетику процесса вакуумной сушки арахиса в аппарате с комбинированным теплоподводом при различных режимах теплоподвода (рисунок 6). Видно, что при оптимальном непрерывном и ступенчатом режимах сушка протекает существенно быстрее, чем при постоянной температуре нагревателей.

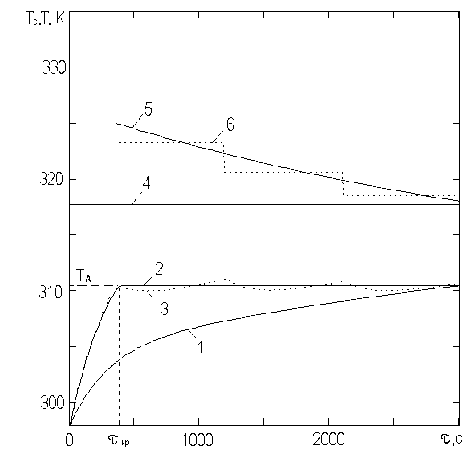
Рисунок 6. Расчетные зависимости температуры материала и нагревателей от времени в процессе сушки арахиса при p = 9,8 кПа: 1 – при постоянной температуре нагревателей Tс = 317 K; 2,3 – при непрерывном оптимальном и ступенчатом тепло-подводе; линии 4,5,6 – соответствующие функции

Figure 6. Calculated dependences of material and heater temperatures on time during the peanut drying process at p = 9.8 kPa: 1 – at constant heater temperature = 317 K; 2, 3 – with continuous optimal and stepped heat supply; lines 4, 5, 6 – the corresponding functions

Заключение

В представленной работе разработана математическая модель тепло- и массопереноса для процесса вакуумной сушки арахиса с комбинированным теплоподводом. Модель учитывает особенности двух основных периодов сушки: периода поверхностного и периода внутреннего испарения.

Проведённое математическое описание позволило получить аналитические и численные решения, описывающие изменение влагосодер-жания и температуры материала во времени. На основе модели исследовано влияние ключевых технологических параметров: коэффициента сушки (K), коэффициента теплопередачи (k т ), удельной поверхности теплопередачи (f t ) и температуры нагревателя (T с ). Результаты вычислительных экспериментов, представленные в виде графических зависимостей, наглядно демонстрируют кинетику процесса и взаимосвязь управляющих факторов.

Сравнение расчётных данных с экспериментальными результатами подтвердило адекватность предложенной модели.

На основе разработанной модели предложен подход к оптимальному управлению процессом сушки. Критериями оптимизации определены качество продукта (ограничение по максимально допустимой температуре материала) и продолжительность процесса. Показано, что оптимальный режим заключается в максимально быстром нагреве материала до допустимого температурного предела с последующим поддержанием этой температуры за счёт программируемого снижения температуры нагревателя. Доказано, что реализация такого режима – как непрерывного, так и упрощённого ступенчатого – позволяет существенно сократить время сушки по сравнению с изотермическим режимом.

Таким образом, работа вносит вклад в теорию сушки термолабильных материалов, предлагая обоснованную математическую модель и практические решения по интенсификации вакуумной сушки арахиса с сохранением его качественных характеристик. Полученные результаты могут быть использованы для расчёта, проектирования и автоматизации сушильных установок комбинированного действия в пищевой промышленности.