Математическая модель трафика с "тяжелохвостным" распределением на основе системы массового обслуживания Н 2/М/1

Известно, что теория массового обслуживания (ТМО) не дает точного ответа при анализе систем с входными потоками, описываемыми «тяжелохвостными» (далее без кавычек) распределениями интервалов между требованиями, то есть систем типа G/M/1/, а тем более систем G/G/1. Весомость хвоста распределения в свою очередь влияет на величину задержки. При этом под хвостом распределения будем понимать функцию Q(x): Q(x) = P(£ > x) = ^(k00)), где ξ – некоторая случайная величина.

Для описания трафика широко используют класс экспоненциальных распределений, включающий подкласс так называемых субэкспоненциальных распределений, куда входят распределения Вейбулла, гамма, логнормальное и гиперэкспоненциальное, имеющие коэффициенты вариации больше единицы (см. рис. 1) и относящиеся к распределениям с тяжелым хвостом (heavy-tailed distributions). На рис. 1 приведены фрагменты хвостов функций плотности этих распределений, а для сравнения приведено классическое экспоненциальное распределение с коэффициентом вариации cT = 1. Слева от классического экспоненциального распределения приведен хвост распределения, сдвинутого от нуля вправо экспоненциального распределения, с коэффициентом вариации cT = 0,5 – «легкого».

На рис. 1 для всех приведенных распределений средние значения равны m_T = 0,25 ; а дисперсии для распределений с тяжелым хвостом равны D_T = 0,25 ; что дает коэффициент вариации интервала времени c_T = 2,0 .

Как видно из этих графиков, даже при сравнительно небольшом коэффициенте вариации распределения c_T = 2,0 заметна тяжесть хвостов затухания приведенных выше функций плотностей по сравнению с экспонентой. Очевидно, что с увеличением параметра c_T весомость хвоста распределения только возрастет.

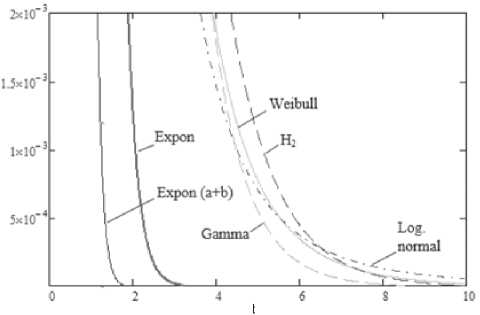
Рис. 1. Графики хвостов функций плотности из класса экспоненциальных распределений

Таким образом, рассматривая только статистические характеристики второго порядка, можно получить определенное представление об отличии распределения времени между поступлениями трафикового процесса от экспоненциального распределения, соответствующего пуассоновскому потоку. С учетом статистики третьего порядка это отличие может только усилиться. Из теории телетрафика известно, что задержки при использовании тяжелохвостных распределений в системах массового обслуживания намного выше, чем при пуассоновском потоке. И наоборот – при использовании распределений с легким хвостом задержки ниже, чем при пуассоновском потоке.

Распознавание закона распределения интервалов времени для его использования в моделях массового обслуживания вызывает большие проблемы, и к тому же трафик, как случайный процесс, имеет свойство постоянно меняться. Поэтому целесообразнее использование числовых характеристик распределения интервалов между пакетами. Для их определения предлагается использовать программу Wireshark [2], к которой авторами написано приложение, позволяющее определить моментные характеристики интервалов между пакетами входящего трафика. Удобство использования данного анализатора обусловлено тем, что он фиксирует моменты времени поступления пакетов агрегированного трафика на уровне долей миллисекунды. Для того чтобы воспользоваться этими результатами, необходим математический аппарат, представленный ниже.

Анализ и расчет среднего времени ожидания для СМО Н2/М/1

Из класса субэкспоненциальных распределений только для гиперэкспоненциального распределения 2-го порядка Н ₂ можно получить явное решение для среднего времени ожидания требования в очереди в системе. Следующим преимуществом данного закона распределения является возможность аппроксимации произвольных входных распределений с его помощью на уровне трех моментов.

Поэтому рассмотрим СМО Н ₂ /М/1, где Н ₂ (см. рис. 1) – обозначение гиперэкспоненциального распределения 2-го порядка времени поступления требований в систему с функцией плотности

a(t) = pX_xe~^x'* + (1 - p^X₂e”^x-^f, (1)

а M – обозначение экспоненциального закона обслуживания с функцией плотности

b(t) = ре”^ц*. (2)

Преобразование Лапласа функции (1) имеет вид

A*^ = p^— ₊ (1-^)J^,  (3)

S + Л|         5 + K^

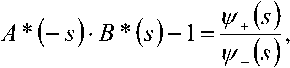
а функции (2) :

B*(s) = -^— s + p

Для исследования системы G/G/1, как известно например из [2], используется интегральное уравнение Линдли:

где ^(5) И (/_(k некоторые рациональные функции от s , которые можно разложить на множители. Функции У'+М И ^_(5) должны удовлетворять определенным условиям согласно [3]:

- для Re(s)> 0 функция (/+(k является аналитической без нулей в этой полуплоскости;

- для Re(s) <  D функция ^_ (^ ) является аналитической без нулей в этой полуплоскости, где D – некоторая положительная константа, опреде-

jp^y^₌< j^C^v м)АС(и), 0;

У ^ 0,

^<0,

где ^(v) – функция распределения вероятностей (ФРВ) времени ожидания требования в очереди; C(w) – ФРВ предельной случайной величины ^{t/ =} !¹S^t/” ^=x« -^ где в свою очередь X_H – время обслуживания n -го требования C

– интервал времени между поступлением требований C„ и c„+1.

Суть решения уравнения (5) спектральным методом сводится к тому, чтобы для выражения

ляемая из условия:

.lm < °° "                              (8)

r—>00 g

Кроме того, функции W₊{^s) и^_(^) должны обладать следующими свойствами:

для Re(s) > 0 lim —= 1;

для Re(s)< 0 lim = —1.

Выражение A * (- 5) • В * (5)-1 = — для распределений (1)-(2) с учетом (3)-(4) имеет вид (10), где коэффициенты

^*(-s)-S*(s)-l

найти представление в виде произведения двух множителей, которое давало бы рациональную функцию от s [2]. Таким образом, для нахождения распределения времени ожидания необходимо следующее спектральное разложение см. (7):

a₀ = 2j2₂ , a₁ = pX_x + (1 - р)Я₂.

В числителе правой части равенства (10) получился многочлен от s третьей степени, и нам остается определить его коэффициенты для разложения многочлена на множители.

Коэффициенты многочлена в числителе дроби приведены в таблице 1.

^n-k^' av-pvx’--U^-i=

\p _ (5)     A_x— s       A^—spAs

\pX_x (5 + Я₂)+(i - p)A₂ (5 + x_x)] • p - (x_x - sX^2 - kk + k k -^Xk -kk+k

p(a₀ -a_xs)-(X_x -sXk ^-5Хх^{/ + 5})

(л_х - ^Xk ^-5’Х/^/ + ⁵)

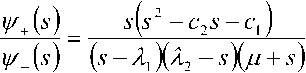
5(5 + 5, X^ — ^2 ) (5-^Xk -^X^+k

/  ^2          ^2 \ где          +  ~^

отрицательный

корень квадратн ого урав нения в числителе дро- 2

„      ^2 ,   / ^2    .                                    - би, ^2 ~--*" Л--*" C1 – положительный ко-

2    2 V 4      1

рень. На рис. 2 показано расположение нулей

(кружочки) и полюсов (крестики) на комплек сной s-плоскости для функции (11).                     К =          = lim 5 + 51 = Д s^°  5 SAlS-U LI

Таблица 1. Коэффициенты многочлена в числителе дроби (10)                                              О c

Степени слагаемых в числителе дроби	Коэффициенты многочлена
5°	0
s1	ц^Д-^+ХгР]-^!^ =
	^1 "^ ^2 — Ц ^ ^2
	-1

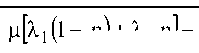
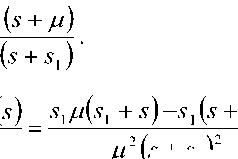
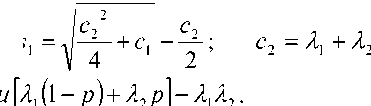
носится к распределениям с тяжелыми хвостами.

Например, у экспоненциального закона A_s = 2.

Файл Справка

Начальный момент 1-го	порядка:	5,097781е-003	А
Начальный момент 2-го	порядка:	3,325837е-004
Начальный момент 3-го Дисперсия: Коэффициент вариации: Асимметрия: Количество пакетов:	порядка:	5,505М9е-005 3,065963е-004 3,434807е+000 1,025441е+001 628183	V

Рис. 3. Результат работы программы-приложения анализа лог-файлов

Рассмотрим результат (13) на примере рассматриваемого входного распределения с весомым хвостом (см. рис. 3). С использованием преобразования Лапласа (3) определим начальные моменты распределения (1):

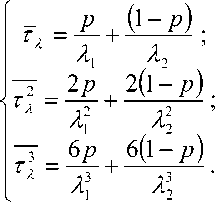
Подставив в систему (15) полученные результаты по начальным моментам распределения интервалов между пакетами (см. рис. 3), для определения неизвестных параметров входного распределения (1): Л], Я₂ и p , получим следующую систему уравнений:

^- + —^ = 5,0978е - 003 ; Х_х       Л-,

• X- + ^—¹ = 3,3258е - 004 ;

Я3      Я2

^ + ^-^ = 5,5050е - 005,

решив которые найдем эти параметры. Решение системы (16) в пакете Mathcad дает следующие результаты: р~ 0,950; Я, «417,985;

Я₂ «17,556. Промежуточные параметры: q «2,429х10³; с₂ «174,441; s₂ «12,962; среднее время ожидания в очереди W «0,073 с.

Определим для сравнения среднее время ожидания для системы М/М/1. В нашем случае загрузка канала составляла Р = 0,75, соответс т венно среднее время обслуживания пакетов г_д «0,0038; интенсивность обслуживания М ~ 263,2 . Тогда среднее время ожидания пакетов W = ^^«0,011 с.

1-/7

Таким образом, модель массового обслуживания с учетом весомости хвоста входного распределения демонстрирует задержку примерно в 6,6 раза большую, чем классическая модель.

Заключение

Для расчета характеристик реального трафика требуется обновленный математический аппарат. Полученные результаты свидетельствуют о том, насколько оптимистичные результаты дает классическая система М/М/1 по сравнению с рассмотренной системой Н2/М/1 в случае высокой весомости хвоста распределения входного потока. Поэтому данный результат с успехом может быть применен в современной теории телетрафика, где задержки пакетов входящего трафика играют первостепенную роль.

Заметим, что распределение (1), содержащее три неизвестных параметра Я], Л_э и p , позволяет с помощью метода уравнений моментов (14) аппроксимировать неизвестные входные распределения на уровне трех первых моментов.