Математическая модель вязкости геологической среды литосферы Земли

Вязкость геологической среды является труднооцениваемым в количественном отношении параметром, одновременно крайне необходимом для исследования и прогнозирования динамики современных геодеформационных процессов в литосфере [1–3]. Сложности, возникающие при его численном оценивании, связаны с непростой взаимозависимостью вязкости, температуры, прочностных, плотностных и других физико-химических свойств геологической среды [4–8].

Основные сложности и решения при создании модели

В ряде научных работ описаны существующие способы численной оценки вязкости, приведены соотношения, позволяющие выполнить эти оценки [1; 4–6; 9–11]. Однако они, как правило, характеризуются весьма неточными, а подчас противоречивыми результатами. В настоящей работе сделана попытка усовершенствовать метод оценки вязкости геологической среды литосферы и предложен новый подход к построению модели для определения величины вязкости. Модель базируется на следующем известном соотношении [8; 10], которое уточнено в целом ряде аспектов, связанных с физикой реальных геодинамических литосферных процессов:

n ( z ) = A k • exp

U a • exp

RT

' 2.5 • P \

VX + 2/3ц J

где z – ось, направленная вертикально вниз; R – универсальная газовая постоянная, равная 8,31 Дж ; зависящие от глубины z: T – температура, P – давление, U – энер-моль■ °К                                                                        a гия активации, λ и μ – прочностные характеристики геологической среды (постоянные Ламе, или модули упругости и сдвига, соответственно); Ak – некоторый коэффициент пропорциональности.

Поскольку в дальнейшем расчеты будут вестись до глубин 80 км, то кривизной Земли пренебрежем.

Определим, какие данные необходимы для осуществления численной оценки вязкости по формуле (1).

Начнем с давления P . Как известно, давление рассчитывается в соответствии с законом P = p gz . Учитывая, что плотность p и ускорение свободного падения g зависят от глубины z , получим:

^P ( z ) = Р ⁽ z ) • g ⁽ z ) • z .                                   (2)

Изменение ускорения свободного падения g с глубиной в слое литосферы от дневной поверхности до границы литосфера – литосферная мантия, т.е. в пределах оцениваемых нами глубин, пренебрежимо мало, поэтому для нашего случая эту величину будем считать постоянной. Следовательно, давление будем рассчитывать по формуле

^{P (} z ) = P ⁽ z ) • g • ^z . ⁽³⁾

В работах [12–14; 26; 27] рассмотрены математические модели и численные методы оценок температуры геологической среды на различных глубинах. Немаловажным фактором является то, для какого типа литосферы проводится расчет температуры – океанической или континентальной. В настоящей статье использованы модели для указанных типов литосфер, созданные в работах [12–14]. В зависимости от типа сформированы два различных подхода к решению задачи по оценке температуры литосферы и, соответственно, две различные математические модели. Температура шельфовой зоны определяется как «сшивка» решений двух моделей.

Рассмотрим прочностные характеристики геологической среды, представляемые модулями упругости и сдвига λ и μ, соответственно. Как известно, упругие модули, скорости сейсмических волн и плотность геологической среды связаны следующими соотношениями [15]:

Vs =

,

Л.

V P                  ,

V P где λ, μ – прочностные характеристики геологической среды (постоянные Ламе, или модули упругости и сдвига, соответственно), ρ – плотность геологической среды, Vp – скорость продольных, Vs – скорость поперечных волн.

Используя (4), нетрудно показать, что глубинное распределение прочностных параметров геологической среды определяется на основании следующей системы урав-

нений:

V j ( z ) =

V P ( z ) =

ц ( z ) P ⁽ z ^),

X ( z ) + 2 ц ( z )

P ⁽ z )

.

Разрешая эту систему, получим:

fp ^{( z} ) = P ^{( z} ) • V S ^{2( z} ),

Уточнение зависимости энергии активации в литосфере

Как известно из химической кинетики, энергия активации U_a представляет собой некоторую пороговую энергию, характеризующую возможность протекания химических реакций. Если энергия участвующих в реакции частиц меньше U_a , то при взаимодействии (столкновении) частиц реакции не произойдет, если же энергия превышает U_a , то реакция начнется [17; 18]. Экспериментально установлено, что существует зависимость, связывающая энергию активации U_a и температуру T :

U ₃ RT- ,

a 10 , где R – газовая постоянная, T – температура (в °K).

Для некоторых однородных слоев геологической среды из экспериментальных исследований также известны значения энергии активации. Так, для однородных слоев верхней коры эта величина составляет 1,34·10 ⁵ Дж/моль, для нижней коры – 2,76·10 ⁵ Дж/моль, для литосферной мантии – 5,3·10 ⁵ Дж/моль [18; 19]. Известны значения энергии активации и для других глубинных уровней. Это дает возможность уточнения величины показателя степени при температуре в соотношении (7).

Для этого положим

R                          U a (T) = b i T b 2 ,

где b 1 = — , b 2 - уточняемый коэффициент.

Построим следующий функционал

n

F ( b 2 ) = Ё ( b^T ? ²

i = 1

— U I fz — 1 aэкспi,(      ,…, n), где Ua эскп i – значение энергии активации, известное по результатам экспериментов.

Потребуем выполнения условия минимума функции (9):

n ₂

^{F (} b 2 ) = E ( ^b 1 ^T i² - ^U a эксп i ) ^ min .                      (¹⁰)

i = 1

Приравнивание к нулю производной от функции F ( b₂ ) по неизвестной перемен-

ной b₂ приводит к соотношению:

n

n

UT^{b 2} ln T a эксп ii       i

T ^{2 b 2} ln T = ^{i = 1}

^∑ i = 1 ⁱⁱ      b 1

,

из которого ее нельзя выразить в явном виде.

Функция F ( b ₂ ) является унимодальной, поскольку на произвольном отрезке она является дважды дифференцируемой, и в любой точке этого отрезка вторая производная функции F ( b ₂ ) положительна [20; 21]. Покажем это.

Последовательно дважды продифференцируем функцию (6), получим:

dFb) = — WT -U 2 = 2(bTb2 -U ,)• b • Tb2lnT + 1 i      aэксп i        11      aэксп1111

d b 2      d b 2 i = i

+2( bTb2 - Ua эксп 2) • Ь • T2 • ln T2 + ... + 2( bTb2 - Ua эксп n ) ' Ь ■ T 2 ■ ln T .(12)

^ F ^ = 2 bTb^{b 2} • ln ² T + 2( bT b² - U a эксп1 ) • b l T 1 ^{b 2} • In T + 2 b²T ₂ ^{2 b 2} • ln ² T ₂ +

∂b22

+ 2( b i T /² - U a эксп2 ) bT ² ln T 2 + ^ + 2 b l ² Tb^{b 2} ln ² T 2 + 2( bT b ² - U a экспз ) bT² ln T n .

Очевидно, что слагаемые вида 2 b 2 T_t ^{2 b 2} • ln ² T_t в выражении (13) всегда положительны. Множители вида b 1 T i^{b 2} • ln T i также положительны вследствие положительности показательной функции, коэффициента b ₁ и логарифма температуры, который может быть отрицательным только при температуре меньше 1°K, что в условиях реальной геологической среды невозможно.

Нетрудно показать, что выражения в скобках в (13) при определенных физических условиях могут быть отрицательными, однако в целом вторая частная производная от функции F ( b ₂ ) будет всюду положительной, что и подтверждает унимодальность этой функции на указанном отрезке. Для нахождения минимума функции (10) по b ₂ можно воспользоваться одним из известных численных методов.

Сделанные численные оценки показали, что b ₂ = 1,857 . Таким образом, поскольку температура зависит от глубины z , соотношение (7) представляется в виде:

1,857

U_n ( z ) = RT ---( z )

.

a           10

Метод оценки коэффициента пропорциональности

Рассмотрим численный метод, позволяющий выполнить оценки множителя A_k в соотношении (1).

Из ряда научных источников известны диапазоны изменения величины вязкости в литосфере [1; 2; 10; 11; 18]. Так, под континентами величина вязкости изменяется в пределах n Land = 10 21 ^ 10 25 Па^с под океанами - n Marine = 10 2 ¹ ^ 10 24 Па-с. Также известно, что на границе Мохо вязкость скачкообразно уменьшается на один порядок и составляет в среднем под континентами 10 ²³ Па·с, под океанами – 5·10 ²² Па·с.

Итак, известны величины вязкости на четырех поверхностях при фиксированных глубинах (обозначим их обобщенно z = z _фикс ):

• 1)    на дневной поверхности (или на океаническом дне);

• 2)    на границе Мохо;

• 3)    непосредственно под границей Мохо;

• 4)    на границе литосфера – литосферная мантия.

  Соответственно, в этих «точках», на основании соотношения (1), можно оценить величины коэффициентов A_k :

  
  

  A k ⁽ z фикс ) =

  
  

  n ( z фикс )

  
  

  exp <

  
  

  ^U a ⁽ z фикс ) R • T ( z фикс )

  
  

  • exp

  
  

  2,5 • P ( z фикс )

  X ( z фикс ) + 2/3 ^ z фикс )

  
  
  
  

Для элементарной, фиксированной по долготе и широте площадки 1 °х 1 ° , распределение коэффициентов A_k ^{( i )} по глубине для четырех «точек» схематично представлено на рис. 1.

На рис. 1 использованы следующие обозначения: H_M – это толщина литосферы от дневной поверхности до границы Мохо; H_L – общая толщина литосферы до границы литосфера – литосферная мантия; H ₀ – глубина расположения океанического дна; H ₁ – глубинный уровень под Мохо (принимается на 1 км глубже самой границы Мохо).

_Ak (1)

_Ak (3)

H L

Дн.

<-------------- пов. Дно	Мохо Под Мохо	Литосфера – литосф. мантия
H 0	H 1
H M		H L – H M

_Ak (2)      _Ak (4)

Рис. 1. Распределение коэффициентов A_k ⁽ i ) по глубине

Тогда для определения величины коэффициента A_k в зависимости от глубины z будет, согласно рис. 1, справедлива следующая система соотношений:

A ⁽²⁾ - A ⁽¹⁾

если z <  H M , то A k ( z ) = A ™ + - k---- k^- ■ ⁽ z - H ₀ );

H M H 0

A (3) - A (4)

если z >  H M , TO A k ⁽ z ) = A k ⁴⁾ + ^{k k} • ⁽ z ^- H M ^- H_xy

H L H M H 1

Таким образом, используя соотношения (16) для Ak, выражение (15) для энергии активации Ua , выражение (6) для прочностных параметров геологической среды, и, учитывая все , вышесказанное для остальных параметров и переменных, в частности для температуры литосферы [12], представим окончательный вид математической модели, на основании которой выполнены расчеты вязкости η в зависимости от глубин- ного уровня z:

n ( z ) = A k ( z ) ■ exp

T 1,857 ( z )

--exp

^ 2.5 -p ( z ) • g • z ^ (X ( z ) + 2/3 ^p ( z ) J

Результаты моделирования

По формуле (17) выполнен расчет распределения вязкости литосферы для различных глубинных уровней в диапазоне глубин от 0 км до 80 км. Так, на рис. 2 представлено эквипотенциальное распределение вязкости в литосфере Земли на глубине 10 км.

Из рис. 2 хорошо видно, что области с пониженной вязкостью совпадают с зонами океанических глубинных тектонических разломов, вдоль которых на глубине 10 км часто происходят землетрясения.

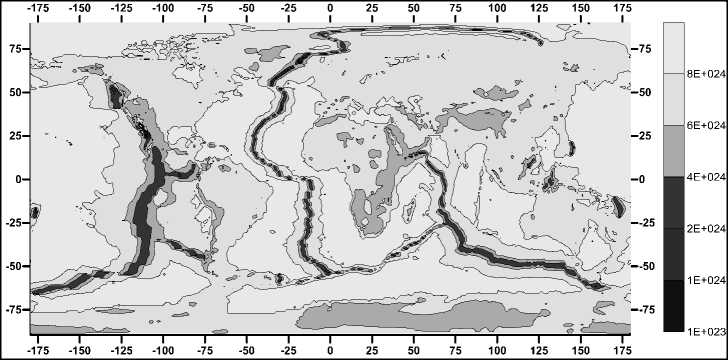
Рис. 2. Эквипотенциальное распределение вязкости (в Па·с) в литосфере Земли на глубине 10 км

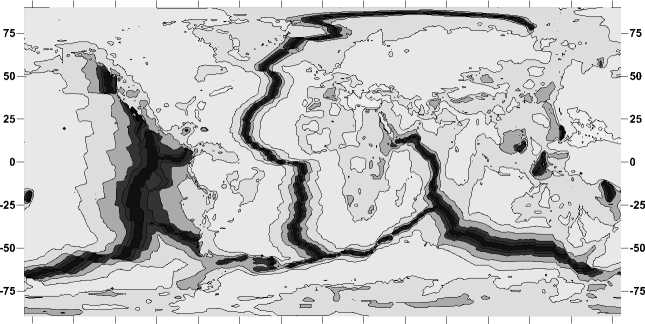
Другие распределения вязкости наблюдаются на глубинах 33 км (рис. 3) и 80 км (рис. 4). Так, на глубинах в 33 км пониженные значения вязкости (рис. 3) становятся более контрастными, указывая на конкретные ареалы зарождения землетрясений на этой глубине. На самом деле, именно здесь произошло около 40% от всех землетрясений, зарегистрированных за все историческое время наблюдений [26; 30].

-175   -150   -125   -100    -75    -50    -25     0     25     50     75    100    125    150    175

1.1Е+024

-175   -150   -125   -100    -75    -50    -25     0     25     50     75    100    125    150    175

Рис. 3. Эквипотенциальное распределение вязкости (в Па·с) в литосфере Земли на глубине 33 км

На глубине порядка 80 км вариации значения вязкости уже не столь значительны, что обуславливается выравниванием температур для океанической и континентальной частей литосферы (рис. 4).

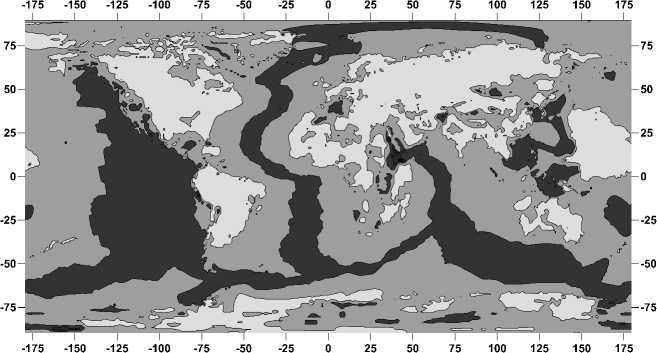
Рис. 4. Эквипотенциальное распределение вязкости (в Па·с) в литосфере Земли на глубине 80 км

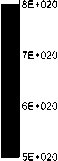
Выводы

• 1.    Вязкость геологической среды, определяемая сложной многофункциональной зависимостью от температуры, давления, прочностных, плотностных и других физико-химических свойств геологической среды, является параметром, весьма трудно оцениваемым в количественном отношении.

• 2.    Математическая модель, численные методы и алгоритмы, описанные в статье, позволяют количественно оценить распределение вязкости на различных глубинных уровнях литосферы Земли. Это представляет собой новый научный результат и значимый вклад в решение проблемы численных оценок характеристик современных литосферных геодеформационных процессов. Информация о распределении вязкости служит необходимыми входными данными для расчета геодинамических деформаций, особенно сдвиговых, позволяя учитывать в них упругую и вязкую составляющие напряжений, тем самым приближая расчетные значения напряжений к их значениям в условиях реальной геологической среды, давая возможность для более точного прогнозирования динамики современных геодеформационных процессов и сейсмических рисков в литосфере [24; 25].

• 3.    Расчетные распределения вязкости литосферы для различных глубинных уровней в диапазоне от 0 до 80 км с шагом в 1 км по глубине позволили выявить их территориальную связь с зонами землетрясений вблизи океанических глубинных тектонических разломов. В частности, на глубинах в 33 км в зонах пониженных значений вязкости произошло около 40% от всех землетрясений, зарегистрированных за все историческое время наблюдений.