Математические методы оценки финансовых транзакций на предмет мошенничества

ВВЕДЕНИЕ И ОБЗОР ЛИТЕРАТУРЫ В настоящее время мошенничество в сфере финансовой информации получило широкой распространение. Огромное количество компаний постоянно сталкивается с различного рода мошенничествами, связанными с финансовыми транзакциями. По данным международной корпорации PricewaterhouseCoopers [1], практически половина компаний из числа опрошенных сталкивались с проблемой мошенничества. При этом ежедневно появляются новые виды мошенничества и одновременно развиваются технологии по борьбе с ними, а область анализа данных на текущий момент является одним из наиболее эффективных средств предотвращения такого рода угроз.

Впервые методы анализа данных для борьбы с мошенничеством стали применять телефонные, страховые компании и банки. Так, например, система оценки мошенничества FICO Falcon [2], основанная на оболочке нейронной сети, успешно применяется в банковской сфере. По данным различных исследований, мошенничество с интернет-транзакциями в несколько раз превышает мошенничество в традиционном секторе продаж (магазины). В 2017 г. FinCert1 установила, что три четверти денег с банковских карт было украдено с использованием ин-тернет-операций.

Для предотвращения несанкционированных действий при совершении онлайн-операций с использованием банковских карт были созданы специальные антифрод-системы. В настоящее время в связи с участившимися атаками на банковские системы интерес к антифрод-системам возрос. Благодаря созданной и усовершенствованной банками системе фрод-мониторинга [3], основанной на принципах машинного обучения, случаи мошенничества с банковскими картами удалось значительно сократить.

Таким образом, с ростом количества мошеннических транзакций у банка, с одной стороны, возникают дополнительные издержки, с другой – платежные системы предъявляют банку-эквайеру штрафы. Именно поэтому все добросовестные участники банковской системы (менеджмент банков, торгово-сервисные предприятия, пользователи банковских карт) заинтересованы в разработке и внедрении качественной анти-фрод-системы [4–8].

В настоящее время существуют разные исследования в области определения девиантных транзакций. Для моделирования финансовых транзакций некоторые авторы использовали метод логистической регрессии [9; 10]. Этот метод применяется в статистике как метод машинного обучения для решения задач бинарного выбора. С помощью логистической регрессии определяют вероятность попадания результата в один из двух классов (мошенническая транзакция или нет). Однако такой подход имеет ряд ограничений и сложностей. Так, например, при построении модели необходимо учитывать наличие нелинейной зависимости между зависимыми и объясняющими переменными, невозможность интерпретации найденных параметров модели, а также приме- нение численных методов для нахождения оценок параметров методом максимального правдоподобия [11].

В процессе построения эконометрических моделей для выявления несанкционированных транзакций также возникают следующие сложности: большой объем информации и неоднородная структура данных для анализа [12]. Как правило, выборка данных является несбалансированной в связи с тем, что в общем объеме всех операций несанкционированными являются 1–2 % тран-закций ² . Для анализа большого объема данных требуются специализированные системы интеллектуального анализа ( Data Mining ), которые предназначены для выявления в наборе данных различных закономерностей и взаимосвязей [3]. Именно на основе Data Mining обычно принимаются стратегические решения. Методы интеллектуального анализа данных в настоящее время все чаще начали использоваться некоторыми учеными для обнаружения мошенничества в области финансовых транзакций. Как показано в работе S. Kirkos , C. Spathis , Y. Manolopoulos [10], Data Mining демонстрирует достаточно высокий уровень точности классификации транзакций и хорошо предсказывает мошеннические операции, а также позволяет избежать проблем, которые возникают при построении соответствующих эконометрических моделей.

В работе А. Kumar и G. Gupta [13] систематизированы результаты применения различных методов выявления девиантных транзакций, в том числе рассмотрены методы опорных векторов, байесовский классификатор, алгоритм случайного леса, метод логистической регрессии. В ходе исследования установлено, что наибольшую точность идентификации девиантных транзакций имеет оценка данных с использованием модели бинарного выбора, а именно логистической регрессии.

J.A. Gomez, J. Arevalo, R. Paredes и J. Nin [14] для выявления несанкционированных финансовых операций и устранения проблем, связанных с несбалансированной вы- боркой, применяли искусственные нейронные сети. По результатам их исследования, использование нейронных сетей позволяет получить хороший результат при выявлении мошеннических операций.

Д.М. Сат с соавторами [15] также провели исследование методов обнаружения мошеннических операций с кредитными картами. В работе рассматривались алгоритмы случайного леса, метод опорных векторов и линейная регрессия. Установлено, что модель, построенная с помощью случайного леса, дает лучшую общую точность по сравнению с двумя другими методами выявления мошенничества.

E.A. Lopez-Rojas , A. Elmir и S. Axelsson [16] применили методы кластерного анализа и нейронных сетей для оценки выявления мошеннических транзакций криптовалюты на примере биткоина. Основная цель их работы заключалась в оценке возможностей применения индикаторов девиантных транзакций для выявления мошеннических операций с криптовалютой биткоин.

Таким образом, результаты проведенного обзора литературы свидетельствуют, что для выявления мошеннических финансовых транзакций наиболее перспективными яв- ляются эконометрические модели (особенно модели бинарного выбора) и модели машинного обучения (искусственные нейронные сети и ансамбли решающих деревьев, а именно метод случайного леса). Поэтому целью настоящего исследования является разработка и определение наилучшей математической модели для предсказания мошеннических операций.

МЕТОДОЛОГИЯ И ДАННЫЕ

В настоящем исследовании для построения моделей и сравнения между собой различных методов были взяты данные, которые являются результатом работы симулятора PaySim [16]. Данные представляют собой синтетически сгенерированный набор с элементами мошенничества. Исходными данными для этого симулятора были реальные данные сервиса мобильных денег африканской страны, которые были представлены в открытом до-ступе ¹ . Выборка включала 1 048 575 наблюдений.

Для построения эконометрической модели использовано девять объясняющих и две зависимые переменные. Описание исходных данных представлено в табл. 1.

Таблица ¹ 1. Описание переменных для анализа

Table 1. Description of variables for analysis

Наименование переменной	Тип данных	Описание
Объясняющие переменные
t	Числовой	Переменная, обозначающая время с периодичностью 1 ч
Type	Факторный	Переменная, обозначающая тип платёжной операции: CASH-IN – прием наличных, CASH-OUT – выдача наличных, DEBIT – списание средств, PAYMENT – платёж, TRANSFER – перевод
Amount	Числовой	Размер транзакции в денежном соотношении
NameOrig	Факторный	Идентификатор человека, совершившего транзакцию
OldBalanceOrig	Числовой	Баланс счета до совершения транзакции у человека, совершившего транзакцию
newbalanceOrig	Числовой	Баланс счета после совершения транзакции у человека, совершившего транзакцию
nameDest	Факторный	Идентификатор человека, принявшего транзакцию
oldbalanceDest	Числовой	Баланс счета до совершения транзакции у человека, принявшего транзакцию
newbalanceDest	Числовой	Баланс счета после совершения транзакции у человека, принявшего транзакцию
Зависимые переменные
isFraud	Числовой	Идентификатор мошеннической (1) или корректной (0) транзакции
isFlaggedFraud	Числовой	Идентификатор обозначения попытки нелегально перевести более 200 000 условных денежных единиц за одну транзакцию

1 Synthetic Financial Datasets for Fraud Detection. URL: (дата обращения: 22.01.2021).

В качестве зависимых переменных были выбраны переменные, которые описывают результат мошеннических операций с транзакциями и используются для обозначения попытки противозаконно провести более 200 000 условных денежных единиц за одну транзакцию.

Перед построением эконометрической модели был проведен первичный анализ данных и определено, какие типы операций связаны с мошенническими. Факторная переменная Type была перекодирована в числовую переменную, которая принимает следующие значения:

• 1,    если операция была CASH-IN (прием наличных),

• 2,    если операция была CASH-OUT (выдача наличных),

• 3,    если операция была DEBIT (списание средств),

• 4,    если операция была PAYMENT (платёж),

• 5,    если операция была TRANSFER (перевод).

На рис. 1 представлено распределение мошеннических транзакций по типу платежной операции. Таким образом, наибольшее количество мошеннических операций проводится через перевод денежных средств (28,41%) и прием наличных (21,54 %).

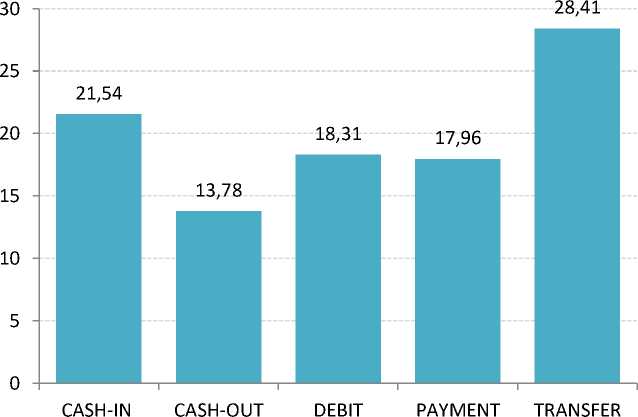
Рис. 1. Распределение доли мошеннических транзакций по типу платежной операции, %

Fig. 1. Distribution of the fraudulent transaction share by payment transaction type, %

В результате корреляционного анализа было установлено, что переменная IsFlaggedFraud зависит от переменных IsFraud и Amount , то есть мошенническая транзакция суммой более 200 000 зависит от идентификатора мошеннической транзакции и размера транзакции. Для дальнейшего анализа можно строить модели с одной зависимой переменной – isFraud .

Согласно корреляционной матрице (рис. 2), в данных присутствует сильная мультиколлинеарность, в частности между переменными oldbalanceOrig и newbalance-Orig, oldbalanceDest и newbalanceDest. Отклонение в данных факторах от линейной зависимости может означать факт мошенничества при проведении финансовых транзакций. Поскольку данные факторы содержат значимую информацию и их нельзя удалить из выборки, проблему мультиколлинеарности необходимо нивелировать посредством применения регуляризации.

Корреляционная матрица type - amount - nameOrig - oldbalanceOrg - newbalanceOrig - oldbalanceDest - newbalanceDest - isFraud - step - nameDest -

0,5

-0,5

-1

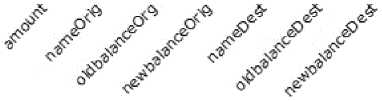
Рис. 2. Корреляционная матрица показателей

Fig. 2. Correlation matrix of indicators

На основании методов корреляционного анализа данных было принято решение выполнить преобразование исходных данных и выделить две новые переменные, обозначающие ошибку в балансе отправителя и получателя. Эти переменные в дальнейшем будут использованы для оценки влияния смещений в балансе при проверке несанкционированной операции.

Новые переменные были рассчитаны по следующим формулам:

balanceOrigErr = newbalanceOrig +

+ amount-oldbal^nceOrg,                (1)

balanceDestErr = oldbalanceDest +

+ amount-newbalanceDest.              (2)

Далее дадим краткую характеристику используемых в данном исследовании методов для предсказания мошеннических финансовых операций.

Эконометрические модели. Поскольку финансовые данные имеют панельную структуру, то в исследовании были рассмотрены эконометрические модели с использованием панельных данных. Для идентификации факторов, оказывающих влияние на факт мошенничества с транзакцией, было рас- смотрено несколько спецификаций моделей на панельных данных: пробит- (probit-) и ло-гит-модели (logit - model) с фиксированными эффектами (fixed effect) или со случайными эффектами (random effect) [18; 19].

Модель со случайными эффектами применяется, если выборка получена случайным образом из генеральной совокупности. Модель с фиксированными эффектами предполагает, что индивидуальный эффект может быть коррелирован с переменными [18]. Смысл фиксированного эффекта заключается в том, чтобы отразить влияние пропущенных или ненаблюдаемых переменных, характеризующих индивидуальные особенности исследуемых объектов, не меняющиеся со временем.

Следующим этапом является сравнение различных моделей на панельных данных между собой и выбор наиболее адекватной из них. Для выбора между моделью с фиксированными и случайными эффектами используется статистический критерий Хаусмана ( Hausman ), нулевая гипотеза которого гласит, что индивидуальные эффекты могут быть случайными, то есть модель со случайными эффектами предпочтительнее [18].

Для сравнения эконометрических моделей также обычно применяют информационные критерии Акаике ( An information criterion - AIC) и Шварца (байесовский информационный критерий, Bayesian information criterion - BIC). С помощью данных критериев можно сделать выбор между различными спецификациями моделей, поскольку наилучшей признается та модель, у которой информационные критерии принимают наименьшее значение [17; 18].

Нейронные сети. Для анализа транзакций также применяют искусственную нейронную сеть. Многослойный персептрон представляет собой некоторое количество слоев, состоящих из нейронов. Определить необходимое количество слоев можно ручным способом или с помощью следствия из теоремы Арнольда - Колмогорова - Хехт-Нильсена [19]:

N' n y< Nw < N • (+1) • (N + N +1) + N ,

1 + log₂( n )      w ^yVN_x          x ^y ’ ^y ₍₃₎

N

N =--^,

N + Ny xy где Nx - количество нейронов входного слоя; Ny - количество о нейронов выходного слоя; n - объем выборки; Nw - количество синоптических связей; N - общее количество нейронов для слоя.

Для правильной работы нейронной сети проводят ее обучение, то есть настраивают веса, задают коэффициенты смещения и некоторые параметры: входные данные (признаки), выходные данные (зависимые переменные), количество итераций (то есть количество раз, которое нейросеть будет обучаться), веса - показатели, позволяющие отмечать степень важности признаков, количество нейронов, количество слоев нейронов, а также производят настройку других параметров для предсказания наилучшего результата, используя определенные ранее входные значения.

Процесс обучения нейронной сети соотносят с решением оптимизационной задачи, в ходе которого возможно обновление модели. Кроме того, устанавливаются пределы задачи (оптимизатор), вычисляется функция потерь для расчета ошибки между реальны- ми и вычисленными значениями. Для минимизации этой ошибки используют алгоритмы стохастического градиентного спуска или среднеквадратичного распространения и получают наилучшую нейросеть.

Случайный лес. Следующий метод [20], который применяется для анализа финансовых транзакций на предмет выявления мошенничества, - дерево решений. Дерево решений - модель, созданная на базе обучения с учителем. С помощью данного алгоритма решающие правила устанавливаются в определенной последовательности, состоящей из узлов и листьев. В состав узлов включены определенные решающие правила, указывающие принадлежность объекта определенному классу. Узлы производят проверку параметров на соответствие определенному признаку обучающего множества. Объекты, находясь в узле, проходят проверку в соответствии с правилом и делятся на подмножества. Далее каждое подмножество снова проверяется на соответствие определенному правилу и делится на очередные множества - и так, пока не сработает определенное условие для остановки алгоритма. Последний узел, в котором не происходит разбиения, становится листом. Лист - некоторое подмножество объектов, удовлетворяющее всем установленным правилам. При построении дерева решения важно разбить обучающее множество на подмножества с правилами в узлах. Процесс продолжают до тех пор, пока все узлы не станут листами.

Случайный лес ( Random forest ) представляет собой алгоритм, основанный на применении ансамбля решающих деревьев и использовании бэггинга (бутстрэп - агрегирование). Для начала из выборки берется несколько элементов с возвращением и формируется несколько подвыборок. Затем для каждой подвыборки строится дерево решений, а конечная модель описывается через усреднение построенных деревьев принятия решений. Чтобы оценить качество разных моделей с точки зрения предсказательной силы, используется коэффициент Джини ( Gini coefficient ) или AUC (площадь под ROC -кривой).

Сравнение различных методов. Для сравнения различных методов классификации финансовых транзакций – эконометрических моделей, нейронных сетей и метода случайного леса – можно воспользоваться такими метриками, как доля верных ответов, точность модели и полнота модели. Указанные метрики формируются на матрице ошибок (табл. 2).

Таблица 2. Матрица ошибок

Table 2. Matrix of errors

Фактические значения	Предсказанные значения
	Y = 0	Y = 1
Y = 0	True negative (TN)	False positive (FP)
Y = 1	False negative (FN)	True positive (TP)

По данной таблице рассчитываются показатели точности и полноты классификации:

Доля верных ответов =

точность =

TP

TP + FP ’

TP + TN

TP + TN + FP + FN ’

TP полнота =        .

TP + FN

Показатель точность интерпретируется как доля объектов, определенных нашим алгоритмом как правильно классифициро- ванные мошеннические транзакции, которые при этом, действительно, являются мошенническими, а показатель полнота пока- зывает, какую долю мошеннических транзакций из всех транзакций нашел предложенный алгоритм. Так как выборка не сба- лансирована, в таких условиях, как правило, применяют показатели точность и полно- та, которые не зависят от соотношения классов, в отличие от доли верных ответов. При этом существует риск возникновения противоречия. Для устранения противоре- чия применяется усредненная метрика, так называемая F-мера, – среднее гармоническое показателей точность и полнота. С помощью F-меры по формуле определяют важность конкретной метрики:

F _p = (1 + в ²) ■

точность ■ полнота

( в ² ■ точность ) + полнота

Параметр в е [0, ^ устанавливает вес точности в метрике, при в = 0 получаем точность модели, при в = 1 — непараметри ческую F-меру, при в = ^ — полноту модели. Наилучшей признается та классификация, при которой F-мера принимает наибольшее значение.

Изложив систему методов и переменных для анализа, в следующем разделе представим полученные нами результаты определения наилучшей математической модели для предсказания мошеннических финансовых операций.

ЭМПИРИЧЕСКИЕ РЕЗУЛЬТАТЫ

П ервоначальная выборка содержит 1 048 575 наблюдений. Выборка была поделена на обучающую (80 % всех наблюдений) и валидирующую (20 % наблюдений). Таким образом, построение моделей произведено на основании одной части выборки, а валидация – на другой. Все расчеты осуществлялись с помощью языка программирования Python . Зависимой переменной является isFraud , которая принимает значение 1, если транзакция мошенническая, и 0, если корректная.

В табл. 3 представлены результаты построения моделей на панельных данных: логит- ( logit- ) и пробит-модели ( probit-model ) с фиксированными эффектами ( fixed effect ) или со случайными эффектами ( random effect ).

Анализ табл. 3 показал, что результаты логит- и пробит-моделей аналогичны. В обоих случаях наилучшими оказались модели с фиксированными эффектами по критерию Хаусмана ( p-value Hausman мало, поэтому модель с фиксированными эффектами предпочтительнее) [21]. Как видно из таблицы, наилучшей моделью можно признать логит-модель с фиксированными эффектами, поскольку для этой модели наименьшими оказались значения информационных критериев Шварца и Акаике [22]. Вывод логичен, поскольку зависимая переменная бинарная, а каждый объект наблюдения (транзакция) обладает своими индивидуальными особенностями. Таким образом, вероятность идентификации мошеннической транзакции достаточно сильно зависит от типа платежной операции и ошибок в балансах отправителя и получателя.

Таблица 3. Результаты эконометрического моделирования Table 3. Results of econometric modeling

Показатели	Логит-модель с фиксированными эффектами ( logit-model with fixed effect )	Логит-модель со случайными эффектами ( logit-model with random effect )	Пробит-модель с фиксированными эффектами ( probit-model with fixed effect )	Пробит-модель со случайными эффектами ( probit-model with random effect )
Type	0,407974***	0,31453***	0,37832***	0,35678***
Amount	4,841*10-6***	4,345*10-6***	4,456*10-6***	4,3578*10-6***
balanceOrigErr	–1,875*10-5***	–1,801*10-5***	–1,756*10-5***	–1,743*10-5***
balanceDestErr	1,567*10-7*	1,891*10-7*	1,428*10-7*	1,418*10-7*
Критерий Шварца	–10 063 518	–10 002 745	–10 001 234	–10 001 158
Критерий Акаике	–10 035 573	–10 001 475	–10 001 174	–10 001 141
Статистика теста Хаусмана ( Hausman )	25 486,48		24 126,47
p-value Hausman	0,0002		0,0003

Примечание: *, **, *** – 10 %, 5 %, 1 % соответственно уровень значимости.

Далее на валидирующем множестве была рассчитана матрица ошибок (табл. 4).

Таблица 4. Матрица ошибок для logit -model

Table 4. Matrix of errors for the logit model

Полученные фактические значения	Предсказанные значения		Всего наблюдений
	Y = 0	Y = 1
Y = 0	209 439	48	209 487
Y = 1	155	73	228

Далее рассмотрим нейросеть. В условиях несбалансированной выборки для построения нейросети необходимо выбрать веса результатам, чтобы на основании указанных весов накладывать штраф на модель. В ходе исследования для правомерной транзакции значение веса получилось равным 0,501, для мошеннической транзакции – 0,499, то есть на функцию потерь, которая применяется при построении нейросети, накладывается некоторый штраф при неверно классифицированной транзакции. Затем расчет корректируется, и нейронная сеть переобучается. Результаты расчетов по обучающей выборке показали, что наша нейросеть будет условно оптимальной, если на входном слое будет семь нейронов, два скрытых слоя с девятью и пятью нейронами соответственно. Для активации входных и скрытых нейронов определена функция гиперболического тангенса. С целью достижения результата в пределах от 0 до 1 на выходе необходим один слой с сигмоидной функцией активации. Функция «бинарная кросс-энтропия» учтена в качестве функции потерь. Матрица ошибок на валидирующем множестве представлена в табл. 5.

Таблица 5. Матрица ошибок для logit -model Table 5. Matrix of errors for the neural network

Полученные фактические значения	Предсказанные значения		Всего наблюдений
	Y = 0	Y = 1
Y = 0	173 742	35 745	209 487
Y = 1	192	36	228

Далее была построена модель с применением алгоритма случайного леса. Для этого на основе функции compute_class_weight определим веса для зависимой переменной. В результате вес для правомерной транзакции равен 0,541, для мошеннической транзакции – 0,459. На следующем этапе проводим обучение ансамбля решающих деревьев. В заданном алгоритме производится расчет дерева решений, при этом усредняется конечный ответ, поэтому построенная модель не может переобучиться, а значит, необходимо обучить модель, увеличив множество решающих деревьев. В пределах эксперимента для анализа отобрано 500 решающих деревьев. Для максимизации в процессе обучения установлен критерий Джини, для выборки применен параметр бутстрапа. После процесса обучения модели при помощи тестовой выборки был проверен результат. Матрица ошибок представлена в табл. 6.

Таблица 6. Матрица ошибок модели на основе ансамбля решающих деревьев

Table 6. Matrix of model errors based on an ensemble of decision trees

Полученные фактические значения	Предсказанные значения		Всего наблюдений
	Y = 0	Y = 1
Y = 0	209 480	7	209 487
Y = 1	46	182	228

Для сравнения используемых для определения мошеннических транзакций методов между собой были рассчитаны следующие метрики: доля верных ответов, полнота, точность модели и непараметрическая F-мера (при в = 1). Результаты вычисленных метрик представлены в табл. 7.

Таблица 7. Сравнение различных моделей

Table 7. Comparison of models

Вид модели	Доля верных результатов	Точность	Полнота	Непараметрическая F -мера
Логистическая регрессия	0,999032	0,603306	0,320175	0,418338
Нейросеть	0,828639	0,001006	0,157895	0,002001
Случайный лес	0,999747	0,962963	0,798246	0,872902

Как следует из табл. 7, доля верно предсказанных ответов, точность, полнота и непараметрическая F -мера на валидирующем множестве наибольшая у метода случайного леса. Таким образом, наилучшей моделью для выявления девиантных транзакций является модель, построенная с помощью случайного леса на ансамбле решающих деревьев, поскольку такие показатели, как доля верно предсказанных результатов, точность, полнота и непараметрическая F -мера, имеют наибольшее значение на валидирующем множестве.

ЗАКЛЮЧЕНИЕ

Рост финансовых потерь из-за увеличения финансового мошенничества приводит к необходимости применения математических методов для анализа реальных данных. В настоящем исследовании рассмотрены различные методы анализа и прогнозирования мошеннических транзакций: эконометрические методы построения моделей на панельных данных (логит- и пробит-модели), нейросетевые методы и методы, основанные на ансамбле решающих деревьев.

Полученные результаты свидетельствуют, что среди эконометрических моделей на панельных данных наилучшей оказалась логит-модель с фиксированными эффектами. В ходе построения нейросети при проведении эксперимента с подбором слоев и нейронов была получена нейронная модель, которая впоследствии протестирована на отлаженной выборке. Проведенный эксперимент на валидирующей выборке показал, что нейронная сеть хуже справляется с предсказанием результата, чем эконометрическая модель. Для построения модели ансамбля дерева решений, основанной на случайном лесе, несбалансированная выборка также была разделена на обучающую и тестовую.

Сравнительный анализ различных методов определения мошеннических транзакций для выявления наилучшего показал, что лучшие значения по критериям доля верно предсказанных ответов, точность, полнота и непараметрическая F -мера имеет модель, основанная на ансамбле решающих деревьев. Таким образом, ансамблевая модель наилучшим образом позволяет предсказать, является ли финансовая транзакция мошеннической.

В перспективе исследование будет сконцентрировано на более глубоком изучении влияния различных факторов банковских операций для проверки финансовых транзакций на предмет мошенничества.