Математические модели гармонических эмоций роботов

В работе [1] приведено определение эмоции робота, которое звучит так:

"Функцию M _;( t ) назовем эмоцией робота, если она удовлетворяет условиям:

• 1.    Область определения      M _;( t ) :

• ^{t e}k - 1 , t 1   ⁰ <  t i - 1 <  t i <™ .

• 2.    M _;( t )    - дифференцируемая на

• 3.    M i ( t i - i ) = 0 и M i ( t i ) = 0 .

• 4.    В области определения существует

( t ₀, T _o) , непрерывная и однозначная функция ^{на [ t}i - 1 , t i ^] .

единственная точка z , такая, что:

z ^ t^ i .

dMf (z )

z ^ t,. и     i-^ = 0".

i       dt

Легко видеть что, например, функция

M_t ( t ) = p sin

TV (t - ti-1

I ti- ti -1          7

для

t G [t;_j, t ],   0 < tt_j < t < , p = const, является эмоцией.

Функцию вида (1) назовем гармонической эмоцией робота.

Математическая модель итоговой гармонической эмоции робота

Согласно работе [2] непрерывное воспитание робота удовлетворяет соотношению

Ri( t) = r( t) + e{t)Ri-, где t - текущее время, t; > t > t^p 0 < ^ (t)< 1. Текущее время удовлетворяет соотношению t = т + tt, где T - текущее время действия настоящей эмоции от начала ее проявления, ti – общее время действия всех предыдущих эмоций, R – воспитание, полученное роботом за время t .

Для робота с неабсолютной памятью справедливы соотношения 0_t ( t_t ) = ^ <  1 - S ,

0 <  д = const <  1 , i - порядковый номер воспитательного такта.

В этой же работе введено определение элементарного воспитания робота, которое записывается равенством ti

Г = j M_t ( t ) dt .             (2)

t i - 1

Нетрудно заметить, что в силу соотношения (2) элементарное воспитание, соответствующее гармонической эмоции робота, имеет вид:

T ri = 2P -L,                 (3)

п где — = tt — tt_j, P - амплитуда гармонической эмоции.

Определение. Гармоническую эмоцию V ( t ) , соответствующую воспитанию робота

Нетрудно заметить, что для положительных амплитуд эмоций справедливо неравенство

A i > P i .

Таким образом, амплитуда A_i итоговой гармонической эмоции робота удовлетворяет равенству (7), а поэтому итоговую гармоническую эмоцию робота можно записать в виде

(             i

v -( t ) = p + E n p P j - i l      J = 2 ^k = j

l

(п sin -(t -ti—i l-.        7

. (8)

Рассмотрим изменение воспитания робота в динамике.

Легко видеть справедливость соотношений

R , назовем итоговой гармонической эмоцией робота на такте i .

Пусть эмоция V ( t ) определяется соотношением

t ri (t) =| Mi «) d( = ti—i

—

-

P -|cos

п

- ( t — t i — i )

-

^Ri =^— P i ^- 7^{os - ( t —} t i — i )

- 1       -

—

v,

— о +

V -⁽ t ) = A i sin ⁽ — ⁽ t ^— t i I ^- i

i — 1

,

+ о ( tP I P ; — i

-

<—ⁱ i — ⁱ

+ E n f k P j — i

J = 2 ^k = j        7

где A_i – амплитуда итоговой гармонической эмоции.

Пусть — = const , т. е., все такты равны.

Нетрудно заметить справедливость цепочки равенств:

R i =—( P i + e p i — i + ор - i p i — 2 + ... + ор ^. о P i ) =

R i = — A i ^-п

cos

^- ( t — t — ) -

—

U. (10)

Приравнивая правые части равенств (9) и (10) друг другу и выражая О ( t ) , получим

формулу

2 -

П

(           i i

= - p. + Z n O k P j — i .

п l     J = 2 ^k = j

Р - А

0 ( t ) = Т---- тг~\-----

I              ^{— i} — i

2 P—i+E MJ l        J=2 k=J

\ ^cos

^- ( t — t i — i ) -

В силу определения итоговой гармонической эмоции и соотношения (4) справедливо равенство ti

t i — 1

= 2 A i ^- .

П

Качественное поведение коэффициента памяти

В общем виде соотношение (11) можно записать в виде

С учетом соотношений (5) и (6) получим формулу

^O i ⁽ t ) = P J^COS

-

2 -

(          ‘ i

\

2 A,~ = - P i + Z WP- i

- П l     J = 2 ^k = J

,

где D i = const <  0 ,

^- ( t — t i — i ) -

— Q,   (12)

которая эквивалентна равенству ii

4 = P i + X P O P — i -

J = 2 k = j

D i =

PA

(

2 P

l

i — i i — i             1

+ ^ n o P —

J = 2 ^k = ^J        7

На рис. 1 приведен общий вид функции (12) при i = 1 , t₀ = 0 , D_x =- 0.1 и - = 10 . Очевидно, что рис. 1 отражает качественное поведение коэффициентов памяти робота во времени для гармонических эмоций и для любого отдельного такта.

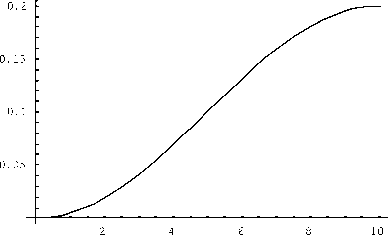
Рис. 1. Качественное поведение коэффициента памяти при гармонических эмоциях робота (по оси абсцисс – время, с; по оси ординат – значения коэффициента памяти)

Нетрудно заметить, что значение О коэффициента памяти в конце первого такта для заданных параметров численного эксперимента приближенно равно 0,2.

Исходя из вышеизложенного и с учетом равенств (6) и (13), справедлива формула

i

4 = P -----•            (14)

i      1 - О

На рис. 2 изображен график изменения амплитуды гармонической итоговой эмоции в зависимости от порядкового номера i такта при коэффициенте памяти О , равном 0.2 и амплитуде гармонической эмоции, равной 5.

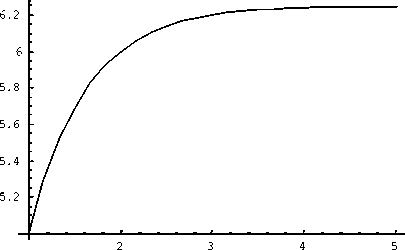
Рис. 2. Изменение амплитуды итоговой эмоции робота (ось абсцисс – порядковый номер такта, ось ординат – значение амплитуды итоговой гармонической эмоции)

Равномерно забывчивые роботы с равноценными эмоциями

Переходя к пределу при i ^ да в обеих частях соотношения (14), получим равенство

Согласно работам [3–6] непрерывное воспитание R_i равномерно забывчивых роботов с равноценными эмоциями удовлетво-

lim A, = i ^да

P

1-О

ряет соотношению

R i = q

1 - О1 - О

где r = q = const , 0 <  О = О = const <  1 ,

i = 1, да .

Покажем, что для равных тактов равноценность эмоций влечет равенство амплитуд гармонических эмоций робота.

Так как эмоции равноценны, то в силу справедливости равенства (3) справедливо соотношение

-

Г = 2 р -i = 2 P -j- = 2 P -^ = r , я J я 7 я j а, следовательно, верно равенство

P = P, = P = const, ij где i = 1, да, j = 1, да.

Так как согласно формуле (14) последовательность A_i является монотонно возрастающей, то справедливо неравенство

A i <

P

i-О

В силу соотношений (6) и (14) формула для описания итоговой гармонической эмоции равномерно забывчивого робота с равноценными эмоциями примет вид

V -( t ) = P

1 - О ТО

I яSin I — (t -t^

I -

Воспитание робота, полученное на основе итоговой гармонической эмоции таких роботов, удовлетворяет соотношению

_     n 1 - О -       Я /      \   .

Rf = -P--। cos — (t - tj i ) -1 fi        1 - о я [ L -      i-1J

Заключение

В силу того, что при создании программного обеспечения роботов разработчик может моделировать любое "психологическое" поведение роботов, то в качестве одной из моделей его эмоции можно использовать гармонические эмоции робота, основные свойства которых описаны в настоящей статье.

Приведенные математические модели динамики коэффициентов памяти робота с гармоническим эмоциями позволяют описывать воспитание робота не только к концу воспитательного такта, но и до завершения такта, т. е. являются попыткой описания непрерывной, а не дискретной модели воспитания роботов.