Математические модели компьютерной зависимости роботов с неабсолютной памятью

В настоящее время в Южной Корее, Японии, США и Сингапуре начались исследования, посвященные разработке алгоритмов поведения роботов в группе. В работе [1] предложены алгоритмы взаимоотношений в группе роботов с неабсолютной памятью. В ней введено понятие внушаемости робота и даны формулы коэффициентов, показывающих степень эмоционального влияния одного робота на другого. Наиболее внушаемым считается робот с большим коэффициентом внушаемости. При равенстве коэффициентов внушаемости двух роботов считается, что, например, первый робот при общении со вторым не изменяет своего воспитания в пользу второго при противоположных по знаку, но равных по модулю эмоциях, и наоборот. Считается, что влияние на общающихся роботов оказывает робот с наибольшим по модулю воспитанием. Этот робот назван роботом-лидером.

В настоящей статье рассматривается непрерывное общение двух роботов друг с другом, при этом один робот, названный компьютером, имеет абсолютную память, а второй робот обладает способностью частично забывать прошлое. Второго робота будем на-

зывать роботом с неабсолютной памятью или просто – "робот".

Будем рассматривать равномерно забывчивых роботов с равноценными эмоциями, влекущими элементарное воспитание q [1].

Определение компьютерной зависимости робота

В работе [2] предложен алгоритм, названный именем грузинского психолога Д.Н. Узнадзе [3], где вводятся понятия эталонных эмоций и воспитательного уровня.

Предположим, что в воспитательном процессе при общении робота и компьютера присутствует только один воспитательный уровень с эталонной эмоцией, влекущей воспитание q .

Согласно работе [1] в этом случае компьютер после эмоциональных тактов, количество которых равно j , получит воспитание _{_} [1]

R _j , удовлетворяющее соотношению

R j = q ,            (1)

а робот с неабсолютной памятью получит воспитание

_R [ _j 1]

= q

1 - 0

1 - 0

где θ – коэффициент памяти робота, 0 e [ 0,1 ) .

Согласно работе [1] роботом-лидером в группе роботов является робот с наибольшим по модулю воспитанием. Поэтому, считая, что робот попадает в компьютерную зависимость, если компьютер становится лидером, введем следующее определение.

Определение. Робот впадает в компьютерную зависимость, если модуль воспитания компьютера больше его модуля воспитания.

вых номерах тактов тем больше, чем меньше коэффициенты памяти. Этот факт говорит о том, что робот с малыми коэффициентами памяти впадает в более сильную компьютерную зависимость, чем робот с большими величинами θ .

Рассмотрим соотношения, определяющие компьютерную зависимость и основанные на моделях алгоритма Д.Н.Узнадзе.

Согласно работе [2] переход на уровень воспитания k + 1 с уровня воспитания k возникает у робота, когда его воспитание удовлетворяет соотношению

Математические моделикомпьютерной зависимости робота

D [ к ] ₌ q , _F ⁽¹ - ⁰ ) ^к - ¹

( 1 — 0 ) ^{к   £}0 ( 1 — 0 ) ^{k — 1} ,

Согласно введенному определению условие компьютерной зависимости робота _{_} [1]

можно записать формулой | R j | >  | R ^[ j ^1] | , которая с учетом соотношений (1) и (2) примет вид

j

I qj\>\q t^I.           (3)

1 — 0

Легко видеть, что соотношение (3) эк-

вивалентно неравенству j >

1 — 0

1 — 0

.

где q – элементарное воспитание робота при равноценных эмоциях на первом воспитательном уровне, ε – восприимчивость робота к воспитанию [2].

В работе [2] введена формула, определяющая относительную восприимчивость α робота к воспитанию, которая имеет вид

ε а =-----.

1 — 0

Легко показать, что в обозначениях α соотношение (4) запишется в виде формулы

1 - 0^j

Введем функцию Г ( j , 0 ) = j --,

1 — 0

которую назовем функцией компьютерной зависимости. Очевидно, что согласно определению, если выполняется условие Г ( j , 0 ) >  0 , то существует компьютерная зависимость робота, иначе зависимость отсутствует. Чем больше значение функции Г ( j , 0 ) , тем сильнее компьютерная зависимость.

Очевидно, что условие Г ( j , 0 ) = 0 отвечает за критическое состояние взаимоотношения "робот – компьютер", при возникновении которого может появиться компьютерная зависимость у робота.

Вычисления показывают, что уже на первом такте [1] при взаимоотношениях «робот – компьютер» возникает это критическое состояние, а начиная со второго такта робот впадает в компьютерную зависимость при любых значениях коэффициентов памяти. Причем значения функции компьютерной зависимости Г ( j , 0 ) при равных порядко-

R [ k ]

α

= q 0 ⁺ q

(1 — 0 ) ^к

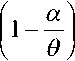
Очевидно, что для компьютера с абсо- _ [ к + 1]

лютной памятью воспитание R при переходе на воспитательный уровень к + 1 можно записать соотношением

_ [ к + 1]        к

R = ЯП, i=1

где j _i – количество тактов на воспитательном уровне i .

На основе вышеприведенного определения можно записать формулу, определяющую компьютерную зависимость робота. Она будет иметь вид

_ [ к + 1] R

> R^{[ к + 1]}| .

Эта формула с учетом соотношений (5) и (6) примет вид

α q^j. > q-^ + q i=1            в

k

i = 1

(1 - в ) k

1 — - I . (7) в J

Легко видеть, что соотношение (7) эквивалентно формуле

Результаты написанного выше можно сформулировать в виде следующей леммы.

Лемма. Если, начиная с некоторого номера L , справедливы соотношения

k

Пл > i=1

a 1 a I

+I 1 I 0   (1 - 0 ) k к 0 J

^ji ^> 1 - в

i = L , да ,

Отметим справедливость неравенства

L - 1

П Л > i=1 i

¹    1 α

(1 - в ) ^L - в

a 1 a I

+I 1 I 0   (1 - 0 ) k к 0 J

α1

— —+г

0   (1 - 0) k

Очевидно, что если будет справедливо неравенство

k

Пл > i=1

α 1

+ в (1 - в) k

1 -

α θ ^,

то будет справедливо соотношение (8).

Запишем соотношение (10) в следую-

щем виде:

то робот с течением времени впадет в компьютерную зависимость.

Получим формулы, позволяющие вычислять количество тактов на каждом воспитательном уровне.

Согласно алгоритму Д.Н.Узнадзе [2] справедливо соотношение

1 A ^j‘+'

R _Hi_ L_ = R [ ^{i + 1]} .       (12)

1 - в

С учетом равенства (5) соотношение (12) эквивалентно формуле

где

D k

D

α

> — θ

k

S j

¹    1 α

(1 - в ) k  ^- в

Покажем, что существуют условия, при которых справедлива формула lim D k = да .

k ^да

Пусть начиная с некоторого значения L 1^_ верны соотношения ji > -—— , i = L , да .

Тогда при условии выполнения неравенства

L - 1

П Л > i=1 i

¹    1 α

(1 - в ) ^L в

можно записать следующую цепочку формул:

lim k ^да

k

Пj i

-

i = 1

> lim k ^да

(1 - 0 ) ^k

-

α

θ

>

α

+

θ

—( 1 - - 1 (1 - 0 )¹ к 0 J

1 - 0 ^{j + 1}

1 - 0

a 1     (, a I

—+--“г I 1 I -

0 (1 - 0 ) i ^{+ 1} к 0 J

Разрешив уравнение (13) относительно j_{t + 1} , получим формулу, определяющую количество тактов ji _{+ 1} на воспитательном уровне с порядковым номером i + 1 , которая будет иметь вид

^ji + 1 = log в

- [(1 - в ) ¹ - (1 - в ) ^{i + 1}] (1 - в)а + в - а

(1 - 0 ) ^k - ^L

( L - 1

к ПЛ

(1 - 0 ) ^L

-

α

θ

J

= да

Легко видеть, что формула (11) автоматически влечет выполнение неравенства (7), а следовательно, и компьютерную зависимость робота.

Исходя из соотношения (14) и леммы можно сформулировать теорему.

Теорема. Если, начиная с некоторого номера L , справедливы соотношения ,     а[(1 - в)1- (1 - в)i+1]      1     .     - logfl--------—----------— >-----, i = l , да, в (1 - в) — + в - а     1 - в ,      ’ ’ то робот с течением времени впадет в компьютерную зависимость.

Очевидно, что верхняя граница T времени, после которого робот впадает в компьютерную зависимость, удовлетворяет равенству

k

T=тЁ j +т =

i = 2

= т

k

¹ + Ё log в i = 2

a[(1 - в)i - (1 - в)i+1] (1 - в)ia + в - a где τ – продолжительность одного такта, k – порядковый номер уровня алгоритма Д.Н.Узнадзе, при котором робот впадает в компьютерную зависимость.

Заключение

Таким образом, в настоящей статье предложены математические модели компьютерной зависимости робота с неабсолютной памятью и сформулирована теорема, позволяющая определять условия компьютерной зависимости при непрерывной работе робота за компьютером (общении робота с компьютером).