Математические модели оценки безопасности роботов для человека

В настоящее время создана математическая теория, разработаны и внедрены в промышленность одноствольные строительные артиллерийские орудия [1]. Применение в практике строительных пушек показало их большую эффективность в нефтегазовом и промышленном строительстве.

Однако основным недостатком созданных орудий является невозможность их использования для застреливания свай на большие глубины при помощи одного выстрела.

Так, например, максимальная величина проникания свай в глинистый грунт с консистенцией 0,5 при использовании установки УЗАС-2, созданной на базе крупнокалиберного артиллерийского орудия М–47, составляет 4 м [1, 2]. Поэтому перед разработчиками строительных пушек встала задача разработать артсистему, способную застреливать сваи на большую глубину. В работе [3] была предложена принципиальная схема многоствольных откатных пушек. На рисунке приведена эта принципиальная схема.

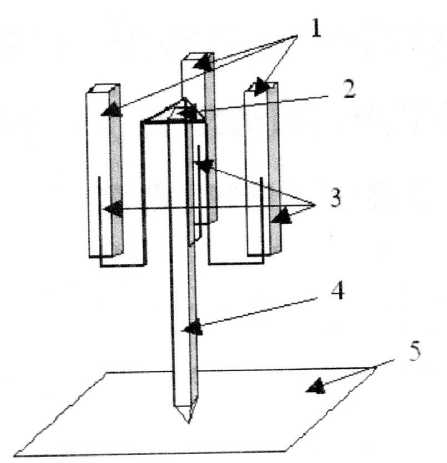
Принципиальная схема многоствольной строительной артиллерийской системы

Работает установка следующим образом. В стволы 1 вставляется фигурный поршень 3 с платформой 2, которая опирается на строительный элемент 4, упирающийся на поверхность грунта 5. Во время выстрела платформа 2 давит на сваю 4, в результате чего свая 4 проникает в грунт 5.

В работе [4] предложены математические модели, основанные на термодинамической теории выстрела и описывающие внутрибалли-стические процессы в стволах 1 при условии, что все артиллерийские системы, объединенные в единый многоствольный строительный комплекс, обладают одинаковыми техническими характеристиками и имеют одинаковые условия заряжания и выстрела. Показано, что для трех одинаковых откатных орудий М–47, объединенных в единую систему, возможно погружать сваи с помощью одного выстрела в глинистый грунт на глубину до 6 м.

В настоящей статье предложены уравнения энергетического баланса в стволах 2 во время выстрела для пушек с различными техническими характеристиками и условиями заряжания, но объединенных согласно рисунку в единую многоствольную артиллерийскую систему.

Вывод уравнений энергетического баланса при выстреле

Для получения уравнения энергетического баланса воспользуемся термодинамической теорией выстрела [5] и предположим, что строительный элемент и фигурный поршень являются недеформируемыми телами.

Пусть n - количество стволов, объединенных в единую систему (см. рисунок), и каждый ствол в системе имеет свой порядковый номер i .

При анализе процесса выстрела во время импульсного вдавливания строительного элемента в грунт необходимо учитывать не только часть энергии пороховых газов, которая превращается в кинетическую энергию поступательного движения строительного элемента, но и энергию, затрачиваемую на совершение другого вида работ. Это позволит установить баланс энергии в каждом из стволов при выстреле.

Определим работу по преодолению силы сопротивления грунта движению в нем строительного элемента, выполненную за счет энергии пороховых газов всех стволов в совокупности.

Пусть сила сопротивления грунта F удовлетворяет соотношению

F = F ( . L a ) .

где v и L - абсолютные скорость и путь сваи (строительного элемента) в грунте.

Тогда энергию, необходимую для импульсного вдавливания строительного элемента на глубину L , можно записать в виде

L a

Z1 = f F(va . xd dx где — = v . t — время.

dt

Очевидно, что кинетическая энергия, которую будет иметь строительный элемент в момент времени t , удовлетворяет соотношению

7 _ mvL

• ²        2    .

где m - масса строительного элемента.

Согласно рисунку стволы артиллерийской системы расположены вертикально и таким образом, что строительный элемент движется вниз. То есть очевидно, что в каждом стволе энергия пороховых газов затрачивается на перемещение откатных частей орудий вверх. Таким образом, совершается работа, которую можно выразить соотношением

Z з. i = QL . i .

где Q - вес откатных частей пушки с номером i . L - путь отката откатных частей пушки с номером i .

Кроме того, энергия пороховых газов в каждом стволе сообщает откатным частям артиллерийских орудий скорости V . Следовательно, кинетическая энергия откатных частей удовлетворяет равенствам

• 7 - MV²

• 4. i          2      .

где M - масса откатных частей с пушки с порядковым номером i в многоствольной системе.

Энергия, расходуемая на преодоление силы сопротивления отката для каждой отдельной пушки. имеет вид

^L _P .i

• Z 5, = J GV . y ) dy .

dy где — = Vi.

dt

Так как строительный элемент во время выстрела движется вертикально вниз, сила тяжести сама выполняет работу Z₆ = qL_a , где q – вес строительного элемента.

Так как в учет выполняемых работ пороховыми газами каждого отдельного ствола не входят работы, выполняемые пороховыми газами других стволов, очевидно то, что эти работы нужно вычесть из совокупности выполняемых работ пороховыми газами отдельного ствола. Соотношения для таких работ имеют вид n La

^Z 7. = Xj P j s j dz ^,

J = 1 0

J * , где Pj и s j – давление в канале ствола с порядковым номером j и площадь поперечного сечения этого же ствола соответственно, dz

— = v . Пусть E - энергия пороховых газов dt a             i в стволе i , за счет которой совершаются ра- боты Z1,Z2,Z3,i,Z4,i,Z5

Тогда очевидны соотношения

E,=X Zj+XZu-Z 6 - Zv-(!)

J=1

Известно [5], что величины E можно аппроксимировать в следующем виде:

P ( W_v + sl )

E = A m ФLk^i i ',(2)

i %            % где i – порядковый номер ствола в системе, которому принадлежит описываемая ниже характеристика, fi - сила пороха, di - показатель адиабаты пороховых газов без единицы, mi - масса заряда, Тi - относительная часть сгоревшего заряда в стволе i, WТ -свободный объем каморы к моменту сгорания в ней части заряда Т(, lt - путь строительного элемента по каналу ствола, li = La + Lp,i.

Заменяя в соотношениях (1) значения работ их математическими выражениями и учитывая формулу (2), получим равенства

A a^ PWWL+sL'=

% i i

Lamv

= J ^{F (} v a , x) ^d x ⁺ — ^{+ Q}i^Lp,i ⁺ 0²

^Mi^Vi ²

^L p , i

+ J G , ( V , , L p№

—

L a

n

—

ql_a - X J S j P j dz , i = 1,n .

j=1 j *,0

Уравнения (3) по аналогии с термодинамической теорией боевых артиллерийских орудий назовем основными уравнениями внутренней баллистики многоствольных строительных откатных артиллерийских систем.

Заключение

Полученные уравнения энергетического баланса при застреливании строительных элементов в грунт из многоствольных артиллерийских систем с различными техническими параметрами стволов и условиями заряжания являются выражением закона сохранения энергии и являются основными при решении задач внутренней баллистики.