Математическое моделирование относительной динамики твердого и жидкого ядер Земли

Третий способ основан на построении математических моделей [4; 5]. Представляется, что все три указанных способа изучения динамики внутренних масс Земли взаимно дополняют друг друга.

В литературе наблюдается широкий разброс значений скорости дифференциального вращения ядра Земли, полученных из сейсмологических данных [6]: от 0,2 до 3 градусов в год с восточным направлением [7; 8], причем в последних работах наблюдается тенденция уменьшения этой величины [9; 10; 11]. Разработана математическая модель планеты, подверженной приливных деформациям, состоящей из двух твердых тел - ядра и оболочки, между которыми находится сферический слой вязкой несжимаемой жидкости [5]. Получено значение средней угловой скорости вращения ядра относительно оболочки в восточном направлении 0,38 минуты в год. Проведена оценка эффектов приливного переноса внутренних масс Земли без учета наличия внутреннего твердого ядра [4].

Постановка задачи. Ставилась задача оценить эффекты переноса масс в ядре Земли приливными волнами. Остальные существенные факторы процесса деформирования Земли (температура, неоднородность мантии и др.) не учитывались.

При построении математической модели представим Землю в виде тонкой оболочки, заполненной вязкой не сжимаемой жидкостью (жидкое ядро); имеется также твердое внутреннее ядро. Для описания движения масс жидкого ядра при достаточно малых высотах приливной волны и малой скорости движения можно ограничиться ползущим приближением, тогда уравнение Навье-Сто-кса линеаризуется и сводится к системе Стокса:

pAv- Vp = 0, Vv = 0, (1) где v(r) - вектор скорости, р(г) - давление, Ц - динамический коэффициент вязкости.

Применим следующий кинематический подход [12]: заранее зададим форму деформируемого тела и граничные скорости, имитирующие движение приливной волны. Для простоты будем считать, что возмущающая масса только одна (в данном случае ею является Луна), и она лежит в экваториальной плоскости Земли. При таких предположениях для упрощения используемых методов можно применять плоскую модель. Правомерность применения плоской модели объясняется тем, что из-за физических условий и симметрии задачи не должно происходить переноса вещества через экваториальную плоскость. Следовательно, явление можно промоделировать только на экваториальной плоскости, причем в условиях плоской деформации. Хотя плоские модели дают только качественные результаты, но для случая однородной Земли они совпадают с полученными экспериментальными лабораторными данными [4].

Форму оболочки в кинематической модели выберем в виде эллипса с малым эксцентриситетом. Форму внутреннего ядра возьмем в виде окружности. На внешней границе (эллипсе) заранее задается граничная скорость, имитирующая направленное движение приливной волны, на внутренней границе жидко сть-твердое ядро задаем условие полного прилипания.

Таким образом, в рамках принятой выше кинематической постановки необходимо решить первую краевую задачу для системы Стокса внутри эллипса с круговым отверстием:

|pVv-Vp = 0, Vv = 0, [ v_r = const, v_n = 0.

На внутренней границе (окружности) задается постоянная касательная скорость, которая является заранее неизвестной угловой скоростью вращения внутреннего ядра Земли. Метод определения этой скорости будет рассмотрен ниже.

Поставленная задача решается методом малого параметра. Естественным малым параметром является эксцентриситет эллипса. После решения краевой задачи можно оценить реально наблюдаемые эффекты.

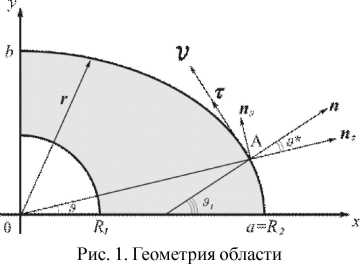
Геометрия метода малого параметра. Для системы Стокса рассмотрим плоскую задачу в двусвязной области S, ограниченной изнутри окружностью L^ радиуса R_y, снаружи - эллипсом Ь₂. Уравнение внешней границы Ь₂ запишем в полярных координатах г и 3 :

Ь              2    1, г= /   2   =, 6 = 1—т,а>Ь.(3)

VI-8 cos 9

Граничное поле скоростей в принятой кинематической постановке имеет следующий вид:

Для угла 31 справедливы соотношения

cos^ , sin3=-—.         (8)

1 ds 1 ds

где ds - дифференциал дуги. Если уравнение границы записать в виде х = х(3) и у = у(3),^то

cos^ =

, sin3, =-

.2 ’

где штрих означает дифференцирование по 3. Согласно (6) можно записать _

v_r = со /?, = const, v_n = О, г eL_v Pr = ^vo = const, v_n = 0, r E L₂,

где v_r,v_n- соответственно касательная и нормальная компоненты скорости, о - заранее неизвестная угловая скорость вращения внутреннего твердого ядра.

Рассмотрим часть области S (рис. 1), в которой а - большая полуось эллипса, Ь - малая полуось эллипса, R^ - радиус внутренней границы, Р₂ - внешний радиус, равный большой оси; угол 3 является полярным углом; угол 3₁ образован нормалью к внешнему эллипсу; 3=3^3 - угол между нормалью и полярным радиусом г; т, п - орты касательной и нормали; п_г, п₉ - орты полярной системы координат.

x = (r0 + Xr_) cos 3, у = (г^э- Xr) sin 3, x ’ = -(r0 + Xr) sin 3 + Xr ’ cos 3, y' = (r0 + Xr)cos3 + Xr’sin3. Учитывая, что cos3* = cos^ -3) = = cos 31 cos 3 + sin 31 sin 3, sin3* = sin(31 -3) = s = in 3, sin 3 - cos 3Z cos 3, из (11), (9), (10) получим

*       r^Xr cos3 = ,                   ,

sin 3 = -

Хг'

Теперь можно выписать разложения cos О* = i + xq+x²c₂+..., sin 3 = 1 + XS^ + X S₂ +...

где

С. =0, C2 =-—sin229,   S. =sin29,     Z1

1        2     2                1                  (14)

S₂ = 4cos³ 3sin3,....

Метод малого параметра. Суть метода малого параметра заключается в том, что решение задачи (2) ищем в следующем виде:

у^^Гу'^г), и=0

или

Проектируя граничную скорость v₀ на внешней границе L₂, которая направлена вдоль т, на направления п_г и п₉, напишем граничные условия (2.2) в полярных координатах:

v_r |_Г=Л2 - —v₀ sin 9*, v_g |_Г=Й2 = v₀ cos 9*. (5)

Для решения первой краевой задачи для системы Стокса в области S с граничным полем скоростей (5) применим метод малого параметра. Естественным малым параметром X поставленной задачи является эксцентриситет эллипса в:

Следуя [13], разложим уравнение внешней границы в ряд по степеням X :

r = ^X"r_n(^ = r_Q+X"r, ; = ^Гг„_+|(9).     (6)

и=0                            и=0

Если взять r0 = R2, то r0 = ^2,',(9) = -/;sin2 9, r2(9) =-Ео sin2 9(l + 3cos2 9)...

(15) vg(r,9) = yVv<")(r,9).

Подставим (15) в граничное условие на внешней границе (эллипсе) (5) с учетом (6):

X^й v^ (г₀ + Хг, 3) = -v₀ sin 3*,

^°           _                        (16)

У X"v^ (г₀ + Хг, 9) = —v₀ cos 9*.

и=0

В формуле (16) разложение правых частей получается с помощью (13). Теперь найдем разложения левых частей (16) в ряды по степеням X:

v^(r0+Xr,9)=_ r 7 _ax г a2V"4r0+Xr,d),

+T--------'-- +

1х=о

Используя (6), найдем коэффициенты этого ряда:

dV^vxr^ _

эх х=0

Г av^oxd) аА

1х=о or Эк )

dr lr=r₀ IV

a^^+Xr,^ ₌ d²x ^x=0 d²v^ (r, 9) Г Эг V dv^ (r, 9) d²r 1

¥r J ⁺ ar a¥ ^x=0

^AA»I„ Г1Ч8нУ^и 2r1№ d2 Г       lr-r0 1 v 7 Qr lr-r0 2 V 7

Подставляя в граничные условия (5) разложения (13) и (17) с учетом (18) и приравнивая выражения при одинаковых степенях X, получаем систему «зацепляющихся» граничных условий для поправок nw . Таким образом, краевые условия на эллипсе сводятся к краевым условиям на границе r0 = R2. Ограничимся первым порядком приближения и выпишем эти условия:

^о)=О,гГ=то;г® = av(0)

= -v0,S1-r1(d)^, or v® = -^(9)^. dr

В силу линейности задачи каждая поправка v'

(”) так-

же удовлетворяет системе Стокса, а граничное условие для него вычисляется из предыдущих поправок и задается на окружности радиуса г = R2. Таким образом, последовательно решая ряд краевых задач для системы Стокса внутри кругового кольца радиусом R2 и внутренним Rv мы можем найти решение в виде рядов (3.1). Когда параметр X достаточно мал, следует ожидать достаточно быструю сходимость этих рядов.

Запишем теперь краевые условия на внутренней границе L_x (окружности):

и=0

v                                X 1 '    '1

_n=0

Отсюда получаем следующее:

Vf 1^=^ = °. и = 0,оо,

• v»0) Ir^03-^, и = 0,(20)

гГи = о,«>1.

Таким образом, для решения исходной задачи с граничным полем скоростей вида (5) получен ряд краевых задач для кругового кольца с внутренним радиусом R^, внешним - R₂ и с краевыми условиями (19) и (20).

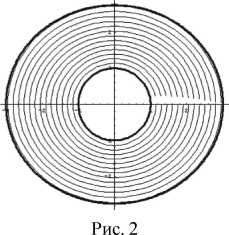
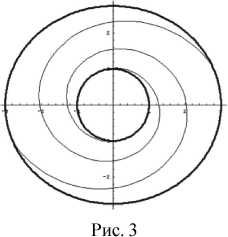
Решение краевых задач методом комплексных функций. Для решения краевых задач для системы Стокса внутри кругового кольца, возникающих в методе малого параметра, применим метод комплексных функций. В [14] показано, что в плоском случае кватернионное представление общего решения системы Стокса переходит в комплексное, выраженное через две аналитические функции cp(z) и y(z) комплексного переменного z = х + iy:

ц(и +zv) =

-z\/(z) + T(^Z),        (21)

где и и v - декартовы компоненты скорости. Такое представление аналогично формулам Колосова-Мусхелиш-вили из теории упругости.

Согласно методу малого параметра в нулевом приближении необходимо решить следующую краевую задачу для системы Стокса в круговом кольце:

Vv(0) = 0, Vp - pAv(0) = 0,

■€4^ = 0, v<°> U^co^,        (22)

^0) L-я = 0, ^ | д = v0,

Г 1Г = К₂      *      9 1Г=Л2 U *

где v0 = const - граничная скорость, имитирующая движение приливной волны.

Решение задачи (22) известно [15] и имеет следующий вид:

v_r =0,

-r²R₂v₀ + R² Г(г² -R²)со + R₂v₀ "I      (23)

r(R2-R2)         '

Задача (22) решена также с помощью комплексного представления (21), при этом комплексные потенциалы имеют вид:

^i^юRi^vo

ф(2 / — 12

2(^

VG0=- 'f ^₂ (A>~v'_ol

Если потенциалы (24) подставить в формулу (21), то после перехода к полярным координатам, получим поле скоростей вида (23).

Согласно методу малого параметра, используя (23) для решения исходной задачи в первом приближении, необходимо решить следующую краевую задачу для системы Стокса в круговом кольце:

Vv(1) = 0,

Vp - pAv⁽¹⁾ = 0,

V® U = o,

•         = 0’                                   (25)

v® 1г=д₂ = ^-vo sin 29,

L_n — Sin -------------------------.

9 'r-K₂                    j^Z _ j^z

Введенные в (21) аналитические функции

хуО) ищутся в виде разложений Лорана с учетом их многозначности в двусвязной области. Коэффициенты ряда находят из систем линейных алгебраических уравнений, получаемых из краевых условий. В первом порядке приближения комплексные потенциалы получены в следующем виде:

/ х 1

W) = b_3 — + b_1- + b1z, zz где ax, a_x, a,, b ,, b ,, b, - выражены через коэффициенты разложения в комплексный ряд Фурье краевых условий из (25).

Полученные комплексные потенциалы

Метод определения угловой скорости движения внутреннего ядра. Угловая скорость движения твердого внутреннего ядра определяется из условия стационарности движения нашей системы, которая заключается в следующем: суммарный момент всех сил М, приложенных к ядру, должен быть равен нулю. Это условие выразим через тензор вязких напряжений а_г$ следующим образом:

М = ^х(агА)^ = ^(^0^6// = 0. (27)

В свою очередь, тензор вязких напряжений можно выразить через тензор скоростей деформации е, зависящий только от угловой скорости ядра о:

^ — 2^^^ —

1 6v_r(to) dv^(to) v^) г Э^ dr г

Подставляя уравнение (28) в (27) и интегрируя по полярной координате d^, мы получаем уравнение с одной неизвестной щ:

271^^

(29) хГя,2[а)0(Х-2)-2а)(Х-1)]+1           "

^+Т?2 [—2(0 + (Do (X + 2)j     J где (Оо -угловая скорость вращения внешней границы.

Из (29), как и следовало ожидать, в нулевом приближении угловая скорость ядра равна внешней угловой скорости о0, т. к. имеем задачу о вращении кругового кольца как жесткого целого, т. е.

®о =^г^

где v₀ = const - скорость на внешней границе (эллипсе), R^ - внешний радиус кольца, в котором решаются краевые задачи (большая полуось эллипса).

Решая алгебраическое уравнение (29), находим угловую скорость внутреннего ядра в виде:

^y-ypr^y+yi

Численные расчеты. После определения поля скоростей ставится задача нахождения траекторий частиц жидкости. Для этого необходимо решить задачу Коши для системы обыкновенных дифференциальных уравнений.

Приведем траектории частиц жидкости после одного полного оборота внешней частицы X = 0,08; а = 3, b = 2,598 (рис. 2); покажем также положения частиц, находившихся на большой полуоси у = 0 в момент времени t = 0, после 30 оборотов внешней частицы Х = 0,08;я = 3, Ь = 2,598 (рис. 3).

Следует прокомментировать переход от кинематической модели к реальной ситуации с приливными деформациями. В кинематической модели наблюдатель находится на вершине приливной волны. Он видит неподвижную область в виде эллипса, граничные точки которого плывут с постоянной скоростью (рис. 2). Реальный наблюдатель движется вместе с границей. С точки зрения этого наблюдателя движение приливной волны - это движение волны деформации по неподвижному кругу. Ког да волна подходит к нему, он совершает вертикальное колебание. Один оборот внешней точки в кинематической постановке соответствует одному обороту приливной волны. Картина, видимая наблюдателю, будет более наглядной, если следить за концами траекторий частиц, которые в начальный момент времени (в кинематической постановке) находились на одном радиусе. Реальный наблюдатель, который в начальный момент времени находился на вершине приливной волны, увидеть эффект переноса внутренних масс под действием приливной волны после ее оборотов (рис. 3).

Оценим скорость вращения внутреннего твердого ядра Земли. Для этого разложим выражение (30) по малому параметру X (до первого порядка):

о = (Оо | 1 + — |. (31)

A

Высота приливной волны для реальной Земли составляет 0,5 м, но так как областью нашего исследования является жидкое ядро с твердым внутренним ядром, берем высоту порядка 0,2...0,25 м. Тогда малый параметр X получается порядка Ю"7. Согласно формуле (31) получаем, что опережение внутреннего твердого ядра составляет 0,39 минуты в год. Эта цифра хорошо согласуется с оценкой из [5], полученной другим, более сложным методом.

Таким образом, на основе кинематического подхода разработана плоская математическая модель приливных деформаций Земли с учетом наличия внутреннего твердого ядра. Разработан метод малого параметра для решения получаемых в модели краевых задач. Получена аналитическая формула для оценки величины угловой скорости вращения твердого внутреннего ядра Земли до первого порядка приближения. На основании результатов можно утверждать, что основной причиной дифференциального вращения внутреннего твердого ядра Земли с восточным дрейфом являются приливные деформации Земли. Получена оценка восточного дрейфа твердого ядра, которая составила 0,39 минуты в год.