Математическое моделирование процесса инфракрасной пастеризации молока

Технология термообработки претерпевает значительные изменения в связи с появлением новых видов оболочек, коптильных препаратов, технических инноваций и других факторов. Тем не менее, подбирая режимы термообработки, необходимо руководствоваться не только рекомендациями изготовителей оборудования или упаковочных материалов, но и теоретическими знаниями о сущности и значении каждого этапа этого процесса.

От соблюдения специфического для каждого продукта температурного р ежима в процессе изготовления напрямую зависят его потребительские свойства, в том числе и вкусовые. Например, при варке и копчении колбас особенно важен контроль температуры как в коптильной камере, так и непосредственно внутри продукта, который является гарантией отсутствия в готовой продукции болезнетворных бактерий, а следовательно, доброкачественности и стойкости мясных продуктов при их долговременном хранении. Для определения эталонных характеристик процессов нагрева и охлаждения колбасных изделий формализуем указанные процессы. Рассматривается батон колбасного изделия наружного радиуса R ʜ , длина которого много больше радиуса (рисунок 1).

Уразов Д.Ю., Шитов В.В., 2013

Рисунок 1 - Схематичное изображение колбасного изделия

Изделие помещается в варочную камеру, в которой обрабатывается паровоздушной смесью с температурой t п = 80°С. Процесс варки колбасы считается завершенным, если температура на оси батона в конце варки достигает 72 °С.

После завершения процесса нагревания колбасное изделие перемещается в камеру охлаждения, где охлаждается воздухом с температурой t ʙ = 8 °С в режиме свободной конвекции.

Цель работы состоит в оценке качества протекания процесса нагрева и охлаждения колбасного изделия по изменению температуры его поверхности в рамках технологического процесса.

Распределение температуры в колбасном изделии определяется уравнением теплопроводности Фурье [1]:

5 1       ( 5 ² 1 1 5 1 1 5 ² 1

— a +1

5т    (d r ² 2 5 r r ² 5ф

521)+ 5z2 v

, (1)

где a = Z/Cp - коэффициент температуропроводности колбасного изделия; Z - коэффициент теплопроводности; С - теплоёмкость колбасы; р - плотность колбасы; г, ф, z - цилиндрические координаты (текущие радиус, угол, высота).

Полагая процесс термообработки осе-

Отметим, что начальные и граничные условия формируются по-разному для периодов нагрева и охлаждения колбасных изделий.

Начальное и граничное условия для уравнения Фурье (3) при нагревании колбасных изделий в процессе варки имеют вид:

1 (0, r ) — 1 0 ,

* — с

⁵ r r — 0

симметричным

— — 0 , а также пренебре-

(5ф J

I51 Л| гая краевыми эффектами I — — 0 I, из (1) по-(5z лучим:

51     ( 5211

— a +

5т    (5r2 25rJ или после преобразования:

— — a —I r— I 5т 5r ( 5r J

^{a ( 1 - 1} n ) ^— 2

5 r

, ^{r —} R H

где a - коэффициент теплоотдачи от паровоздушной смеси к поверхности колбасного изделия; Z - теплопроводность колбасного изделия.

Граничное условие (5), записанное из условия симметрии температурного поля на оси (6), является граничным условием третьего рода для поверхности колбасного изделия.

Решение для нагревания колбасного изделия в процессе варки имеет вид [1]:

м

О —Z- n—1

----Г ₂ ² J ¹⁽ M n )₂ ------1 ■ J _o ( M„R ) ■ exp( - M²F _o), M n [ J ²( M ) + J 1 ²( M ) ] n ’    ¹ n

О —

1 -

¹ 0 ^-

t

— - безразмерная температура, t _n

где J ₀ - функция Бесселя первого рода нулевого порядка; J 1 - функция Бесселя первого рода первого порядка; M _n - корни характеристического

уравнения. J 0( M ) M —, (8) J 1( M ) Bi где B, — —- - число Био; R —--безразмер-i х                    Rn

Как следует из характеристического уравнения (8), значения M_n зависят от числа Био. Таблица для первых шести корней M_n в зависимости от Б ; приведена в [1].

В конце процесса нагревания (обычно при F0>0,3) реализуется так называемый регулярный режим теплообмена [2], при котором в решении (7) можно пренебречь всеми слагаемыми ряда, кроме первого:

ат ный радиус; F —    - число Фурье.

⁰ R n

о «

2 J 1 ( M 1 )

M 1 [ J 0 ²( M 1 ) + J 1 ²( M 1 ) ]

■ J 0 ( M 1 R ) ■ exp( - M 1 ² F 0 )

Распределение температуры по радиусу колбасного изделия существенно влияет на процесс её последующего охлаждения.

Рассмотрим предельные распределения темп ературы по радиусу колбасного изделия в конце процесса нагрева.

При достаточно высоком коэффициенте теплоотдачи а и малом наружном радиусе изделия R_H значение числа B , > 50,0. В этом случае перепад температуры на границе пренебрежимо мал по сравнению с перепадом температуры в колбасном изделии (рисунок 2a). Температура поверхности t_c ~ 1_п,, и граничные условия III рода вырождаются в граничные условия I рода.

В этом случае из (8) следует:

J о ( M , ) « 0,            (10)

M 1 « 2.40            (11)

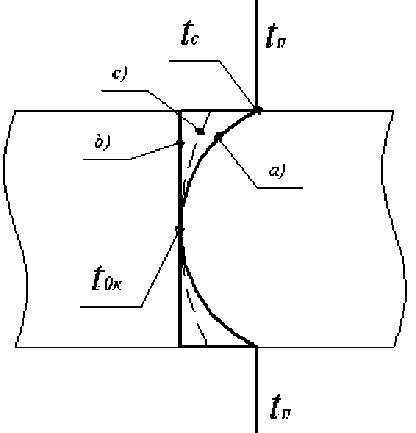
Рисунок 2 - Распределение температуры по радиусу колбасного изделия в конце процесса нагрева ( a - для Bi >50,0; в - для Bi < 0,1; c - для 0,2 < Bi < 50,0)

Решение (7) преобразуется к виду:

О « - • J ₀ ( M 1 R ) • exp( - M 1 ² F _o ) (12)

M 1 J 1 ( M 1 )

В случае малого значения коэффициента теплоотдачи, когда B i < 0,2, температурное поле в колбасном изделии однородно (рисунок 2b). При всех остальных значениях 0,2 < B i < 50,0 кривая с распределения температуры по радиусу в конце процесса варки лежит между кривыми a и b (рисунок 2).

Очевидно, что при последующем охлаждении колбасных изделий температура её поверхности в случае а будет несколько выше, чем в случае b.

После завершения процесса варки колбасное изделие помещается в помещение с температурой воздуха tв, где охлаждается в режиме свободной конвекции. Коэффициент теплоот дачи определяется из критериального соотношения [2]:

Nu = 0,5 - ( Gr • Pr )⁰²⁵,         (13)

gd    t. — t где Gr = — ---c—— - число Грасгофа;

и ² t _c + 273

g = 9,81 м/с ² - ускорение свободного падения; d = 2R n - диаметр колбасного изделия; и - кинематическая вязкость воздуха; t c - температура поверхности колбасного изделия; Pr - число а • d

Прандтля для воздуха; Nu =---- - число

Л ,

Нуссельта; а - коэффициент теплоотдачи; Х в -теплопроводность воздуха.

Коэффициент теплоотдачи:

а = 0,5 ^^ ( Gr • Pr ) ^0.25 (14) d

Поскольку температура tс существенно изменяется в процессе охлаждения, коэффициент теплоотдачи также сильно изменяется - в два и более раз (рисунок 3). Граничное условие (6) становится нелинейным, что не позволяет воспользоваться известными решениями теплообмена для цилиндра, полученными для постоянного коэффициента теплоотдачи а.

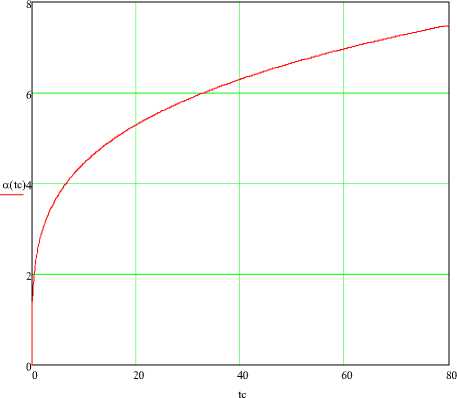
Рисунок 3 - Зависимость коэффициента теплоотдачи колбасы от температуры поверхности, R_H = 0.04 м, t в = 0 °С

Для решения задачи об охлаждении колбасного изделия воспользуемся численным методом [3].

Перейдём от дифференциального уравнения (3) к его дискретному аналогу на сетке с

а

•

постоянным шагом (рисунок 4) с использованием явной схемы.

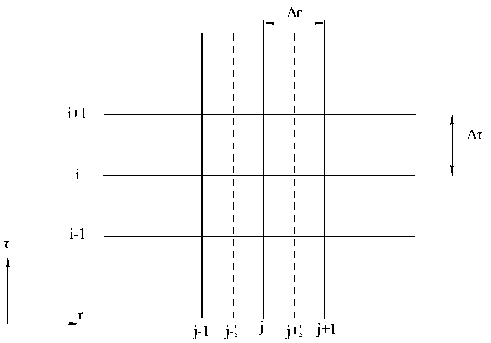
Рисунок 4 - Фрагмент дискретной сетки.

ti+1, j ti,j

a r

д t r • д r

(a r)2

•

A r

r

•

ti , j + 1

—

t . i . j

—

A r

r ₁

•

t i , j      t i , j — 1

A r

или

где F 0 c

б t

—

дт

Ат

,

ti + 1, j

—

t- - i. j

a

Ат

( A r )² L

t i . + 1, j      t i . j ^{+ F} 0 c

t, + — A r j 2

aAT

-—— - сеточное число Фурье.

( A r ) ²

Выражение (20) позволяет вычислить значение температуры в узле j на последующем шаге по времени 1 +1, если известны значения

температуры в трех узлах по радиусу на предшествующем шаге по времени t₍₁ j_ ₁ ) , t^ j) , t < _I j ₊ i) .

Для обеспечения устойчивости вычислительного процесса необходимо шаг по времени Ат выбирать достаточно малым, так, чтобы выполнялось условие:

Fc s 7

Температура в узле J 1 (на наружной поверхности) определяется из (6) с учетом (14):

9. , i, j 1

—

9 , , i, j1—1

—

A r

0.5 • 4 gd

•

Рг

0.25

Xd и

•9

1.25

j 1

,

^r 1 ^{( t}i . j + 1

j + 2

t i , j ) r _— 1 ^{( t}i . j ^j 2

—

t i,j — 1 ) ’

где 1 - номер шага по времени т; j - номер шага

по радиусу г; Ат - шаг по времени; Аг -

радиусу.

r

, 1 A 1 = r j ⁺ ^ ^{A r} ,

r 1 = r j ^j 2

—

— A r , 2

После подстановки (12), (13) (17), (18) в уравнение (3) получим:

i , j + 1

—

t .

i , j

—

с

шаг по

учётом

t .

< i , j

—

t i , j - 1 ) ’

ti , j — 1 ) ’

Из (22) можно получить рекуррентную формулу для вычисления температуры на гра

нице ⁹ i , j 1^:

i , j 1

i , j — 1

1 + A • 9, , i , j 1

где

A = 0,5 •Ar • ^в-X

g • Рг и ² d ( t _B + 273)

0,25

где 9 = t — t в - избыточная температура.

Дискретный аналог граничного условия (5) для оси:

t i ,0 = t i ,1 ⁽²⁵⁾

Начальное распределение температуры для процесса охлаждения колбасных изделий принимается по конечному распределению периода нагрева.

В ходе вычислений определяются температуры на оси и поверхности колбасного изделия во всех узлах по времени i . Наибольший интерес представляет температура поверхности колбасного изделия, поскольку по ее изменению оценивается процесс нагревания и охлаждения.

Ниже приводится пример расчета процесса термообработки колбасных изделий для следующих исходных параметров: R_H =0,04 м; t₀ =20С; к = 72^ОС; р =994 кгМ ³ ; с =3600 Дж/(кг^К);

t n =80^ОС; t e =0^ОС; р в =1,13 кгМ ³ ;

X =0,4

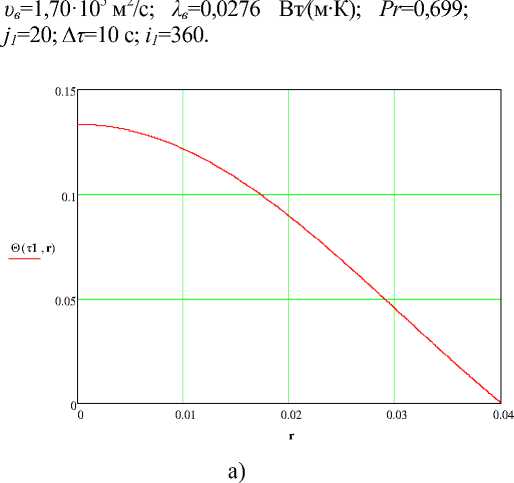
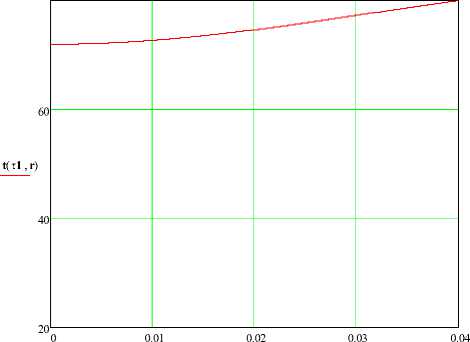
Рисунок 5 - Распределение температуры по радиусу в конце процесса нагрева. а) - в безразмерном виде, б) - в размерном виде

На рисунке 6 показано распределение температуры по радиусу в конце процесса охлаждения колбасного изделия воздухом (при

В результате расчетов определено время варки колбасного изделия, при котором достигается температура на оси t_K0 =72°С: т 1 =6178 с (~ 1ч 43 мин), распределение безразмерной и размерной температуры в конце процесса варки (рисунок 5).

r

б)

т к =3600 с). Зависимость температуры центра и поверхности колбасного изделия от времени в процессе охлаждения представлены на рисунке 7

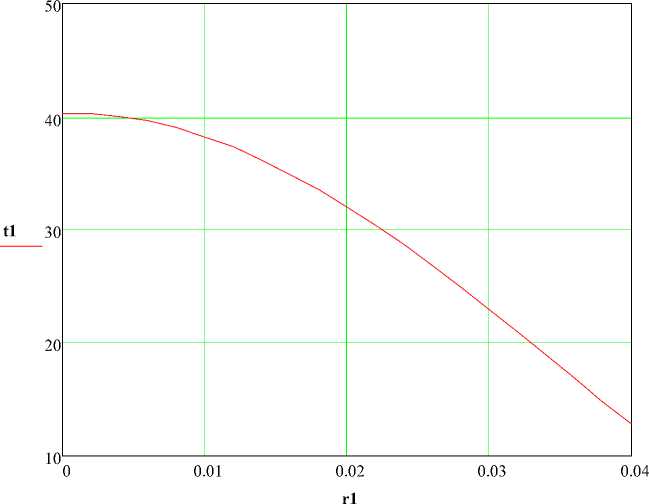
Рисунок 6 - Распределение температуры по радиусу в конце процесса охлаждения.

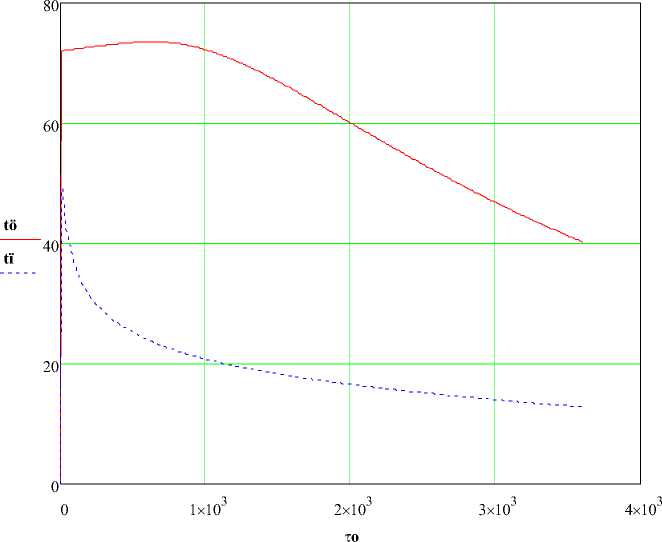
Рисунок 7 - Зависимости температур центра и поверхности колбасного изделия от времени в процессе охлаждения.

Полученные зависимости позволят с высокой долей точности судить о распределении темп ературы по радиусу колбасного изделия, основываясь только на темп ературе его поверхности, что открывает возможность применения новых методов контроля и диагностики технологических процессов.