Математическое моделирование процесса микронизации зерна

B процессе микронизации зерна влага испаряется, в основном, в периоде убывающей скорости сушки [1].

Слой зерна, находящийся на поверхности транспортера микронизатора, будем рассматривать как горизонтальную пластину толщиной 2 R . Bcледствие того, что в процессе микронизации с поверхности зерен испаряется незначительное количество влаги

(в пределах 2-7 %) будем считать пластину постоянной толщины.

Начало системы пространственных координат поместим в произвольную точку (рисунок 1). Слой зерна, который рассматриваем как горизонтальную пластину толщиной 2 R , движется горизонтально, а падающий на него лучистый поток примем за перпендикулярный.

Ось координаты z направим параллельно потоку инфракрасных лучей, а координатную плоскость (у , х ) расположим перпендикулярно оси z и параллельно поверхности зерна (как мы увидим ниже, координаты у и х не участвуют в уравнениях, описывающих процесс сушки).

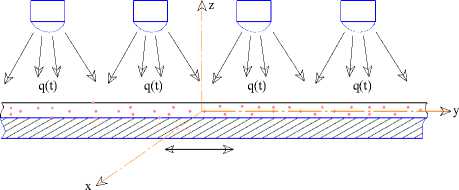
Рисунок 1. Расчетная схема процесса микрониза-ции зерна

Изменение температуры T и влагосо-держания U в процессе сушки описывается системой дифференциальных уравнений теп ло- и массопереноса:

\аи „ , „__

—=ь v и+b5V т+s

, дт

«д т  ^sr д и

= a V T + .

,дт          c дт

где

_V- д ² д ² д ² д х ² д у ² д zz

- оператор Лапласа,

a - коэффициент температуропроводности продукта, м2/с, b - коэффициент массопереноса (диффузии), м2/с, 5 - термоградиентный коэффициент, s - коэффициент фазового пре вращения, r - удельная теплота испарения воды, кДж/кг; c - удельная массовая теплоемкость вещества, кДж/(кг-К).

Поскольку в процессе микронизации структура зерна претерпевает изменения, то для достижения точного решения уравнений необходимо учитывать изменения теплофизических, оптических и др. (плотности, температуропроводности, теплоемкости) параметров. Значения коэффициента температуропроводности a, коэффициента теплопроводности Я и массовой удельной теплоемко сти c учтем при различных значениях температуры и влажности зерна. Коэффициенты поглощения, отражения и пропускания лучистого потока будем считать постоянными.

В связи с доминирующим перемещением влаги вдоль оси z, высоким градиентом влаго-содержания, незначительным внутренним вла-гопереносом по координатам у, хи последующим испарением, температура и влагосодер- жание не зависят от координат у, х: следова-

тельно, уравнения (1) принимают вид:
	д и ,а 2 и ,^ а 2 т д и --- b—т + Ь5—т + s --, дт д z 2       д z 2 дт
	д T    д 2 T s r д и - a +        . _дт    д z 2    c дт	(2)

В уравнение теплопереноса необходимо добавить слагаемое, отвечающее за инфракрасный нагрев. Пусть мощность падающего на вещество лучистого потока равна q (т). То- гда мощность поглощенного потока в точке вещества с координатой х равна:

q (т)- Aq (т) exp (k (R - z)), где к - коэффициент инстинкции (коэффициент ослабления луча); А - коэффициент поглощения.

Ввиду малой толщины зерна ослабление луча в толще продукта можно считать линейным по координате z .

д T     д ² T s r д U 1 ,

— - a— у +---+— Aq .

дт    д z ² c дт с р

При точном решении уравнений необходимо учитывать зависимость коэффициентов от времени. С учетом этой зависимости система уравнений может быть записана так:

«

(z ,т)- b(т      (z ,т) + b(т)5 (т ti (z ,т) + дт            дz                  дz д U,

+ s ( z ,т )----( z ,т )

V ’ дт V ’

'д T, ,     , , д² T, , ^s ( z^,т ) r дU, ,

т ⁽ z , ^{т )- a ( т}    ( ^{z , т ) +}— т ^{( z , т )+}

P w ⁺ P s U ^{( z} , ^{т )}

[ c ( т ) P s P w ( и ( z , т ) +1 ) q ^(т)

Уравнение (5) можно переписать в эквивалентном виде (учитывая, что s ( z , т ) # 1, равенство означало бы, что влага испаряется с поверхности пластины):

ди(z,т)= b(т)    "■(z,т)+ дт         1 -s(z,т) дz2

+

b (т) 5 (т) д2т

1 - s ( z , т ) д z ^{2 (} , ⁾ .

В начальный момент процесса микрони-зации ( т - 0) температурa и влагосодержание постоянны:

T ( z ,0 ) ^ T o , и ( z ,0 ) ^ и 0 .

Ввиду малой толщины зерна, пренебрегаем процессами, происходящими на краю зерна, поэтому граничные условия будем записывать лишь для z = ±R , то есть фактически рассматриваем задачу для бесконечной пластины.

Пренебрегая бародиффузией и термо-влагопроводностью (поскольку их вклад становится заметным лишь при температурах порядка 100 °С, запишем граничное условие для уравнения массопереноса в виде условия третьего рода на поток влаги, испаряющейся через поверхность пластины:

. d U ,

- ^A m ( ^{R, т} ) — ( ^{R , Т} ) = ^в ( R ^{, Т} ) • о z

P s P w ( U ( ^{R, T} ) + 1L             .

' P w + P s U ( R, T ) ^{( U ( R} ' ' ^{) —} U ср ) ■      ⁽⁸⁾

Приравняем коэффициенты при одина

ковых степенях z :

t .( т ) = 2 а д ( т ) + Aq ^{( P} - ^{+ P} s u o^{( T}» О              1 2

P s P w^C 1 ^{(1 +} u o ^{( т} ))

Ы т ) = 2 -aqL

P s P w^C1

. P w ⁺ P s^Uo ^{( т} ),

• ⁶ —i--- T—4 4 ^{( т} ) +

• ^{1    +} u o ^{( т} )

+ — ^Ps--^P w y U ₂ ( т ) Ч ( т )

(1 + Uo ( т ))² 2^V,2V\

. (10)

Изменения коэффициента теплопроводности А примем равным приблизительно А « Д = 0,294 Вт/ (м ■ К).

где A m - коэффициент массопроводности,

в - коэффициент массоотдачи, U ср - влаго-содержание окружающей среды.

В периоде убывающей скорости сушки коэффициент температуропроводности а ме

няется незначительно, поэтому в этом периоде значение коэффициента температуропроводности постоянно, т. е. а ® а = 15,57 ■ 10 ^{— 8} м² /с.

В силу симметрии задачи по z (пластина однородна и симметрична, воздействие постоянно по z , то есть тоже симметрично) функции U ( z , т ) и T ( z , т ) четны по z : это означает, что ряды будут содержать только слагаемые с четными степенями z . Подставив эти выражения в систему уравнений и начально-краевых условий, затем отбросим слагаемые степени выше 2 как пренебрежимо малые, то есть функции U и R будем приближенно искать в виде.

Уравнение массопереноса с учетом допущения s (z , т ) = 0 принимает вид:

Аналогично, теплоемкость примем равной с « с , = 2107,52 Дж /(кг ■ К).

Уравнение теплопереноса (8) содержит

P + PsU(z,т)     , / X слагаемое —-----;—;—/—Aq (т), кото- c(т)PsPw(U(z,т) +1)

рое необходимо разложить по степеням z :

Pw + AU (z,т )   Aq , c (т ) Ps Pw ( U ( z, т ) + 1)

Aq ( P w ⁺ P s ( ^U 0 ( ^T ) ^{+ U} 2 ( ^T ) ^{z 2} ) )

P s P w c (^T ) ( ^U 0 ( ^T ) ^{+ U} 2 ( ^T ) z ^{2 +} 1 )

Aq

P w + P s u 0 ( ^Т )

л

P s P w c ( ^Т ) ^ ¹ + ^U 0 ( ^Т ) + ( 1

P

—

■ 0

P w     / X 2

■ ^U 2 ( ^T ) z

(мы учли, что q ( т ) = q = const).

После упрощения правой части и отбрасывания слагаемых порядка выше 2, по z уравнение приобретает вид:

. / х , . / х 2 ~ , , X , Aq ⁽ P_w ⁺ Ps ^и₀^(т )) , t 0 ^{( т} ) ⁺ t 2 ^{( т} ) z = ^{2 а} 1 t 2 ^{( т} ) ⁺------------- — ⁺

P s P w ^c 1 ^{(1 + U} o ^{( т} ))

+ 2 A^a 1 q

P s P w c 1

, P w ⁺ P s ^u o ^{( т}).

• 6—-- —-t 4 ^{( т} ) ⁺

• ^{1    +} u o ^{( т} )

^P s ^{— P} w

(1 + U o ( T ))²

u 2 ^{( т} ) t 2 ^{( т} )

.                                             .

U o ( т ) + U 2 ( т ) z ² = 2 b ( т )( U ₂( т ) + 6 и ₄( т ) z ²) + + 2 b ( т ) 5 ( т )( 1₂( т ) + 6 1 ₄( т ) z ²)                    .

Приравнивание коэффициентов при одинаковых степенях z дает систему:

U o ( т ) = 2 b ( т ) u ₂( т ) + 2 b ( т ) 5 ( т ) 1 ₂( т ), .

и 2( т ) = 12 b ( т ) и ₄( т ) + 12 b ( т ) 5 ( т ) 1 ₄( т ).

.                                       (11)

Значения коэффициента массопереноса (диффузии) b и термоградиентного коэффициента 5 будем считать постоянными.

Выпишем значения констант, участвующих в системе уравнений тепло- и массопереноса. Мощность теплового потока примем равной q = 35 кВт / м². Коэффициент поглощения для зерна пшеницы в соответствии с экспериментальными данными примем равным А ~ 0,75. Значение плотности влаги примем равным плотности воды: P w = 1000 кг/м³. Зная плотность продукта при исходной влажности 17 % и при влажности 8,9 %, найдем плотность абсолютно сухого вещества P _s = 905 кг/м³. Коэффициент диффузии b примем равным b = 2,71 - 10 - ¹² м² /с. Как показывают эксперимент, термоградиентный коэффициент 5 в периоде убывающей скорости сушки весьма

мал при вышеуказанных значениях влагосо-держания, поэтому им пренебрегаем.

Значения температуры Т ср и влагосодер-жания U ср постоянны. Значение Т ср = 95 ° С для процесса микронизации пшеницы.

Подставляя в уравнения (1), (2) ив граничные условия известные значения констант, задача сводится к построению функции влаго-содержания. Поскольку температура, в силу нагрева, выравнивается практически по всей _                             д2 Т толще продукта, слагаемое, содержащее —т-, дz2

из уравнения массопереноса пропадает, и это уравнение приобретает вид lU ( z,т ) = b (т )     (z,т ) + £( z,т ) 'У (z,т ) (12 )

дт             дz2               дт или д U .      b (т) d2U     .

^{( z , т} ) = 1Т        ^{z , т} ).     ( ¹³ )

дт         1 - е (z, т ) д z

Коэффициент b ( т ) будем считать постоянным и равным b = 2,71 - 10 м /с; величину £ (z, т ) положим равной 0,3. Коэффициент

b^{( т} )   = 3,87 - 10 ^{- 12}

1 - е ( z , т )

м² /с обозначим Б .

Начальное условие приобретает вид

U ( z , т о ) = C о + C 2 x ²,

где константы Со, С2 могут быть найдены из среднего значения U(то), определенного экспериментально, и из граничного условия. Принимая U (то) = 0,5 (примерное значение вла-госодержания в момент, когда температура продукта постоянна), получаем соотношение с0 R+-с2 R3 = о,5.

Граничное условие в данном случае имеет вид

A m ( R, т ) O U ( R, т ) = в (R, т ) ^{PP(U ( r} R ^ ^{1 +} 1) - д z                  P w + P s U ( R , т )

- ( U ( R , т ) - U _cp)                             ( 15 )

д U _{( R т} ) = в ( R, т ) P s P w ( U ( R, т ) + 1) _- ^д z   ’      ^A m ^{( R, т} ) P w ⁺ P s ^{U ( R, т} )

- ( U ( R , т ) - U cp ).                     ( 16 )

Для коэффициентов массопроводности A m ( R , т ) и массоотдачи в ( R , т ) возьмем постоянные значения:

A m ( R , т ) = 1,6 - 10 ^{- 3} кг/(м - с), в ( R , т ) = 2 - 10 ^{- 5} м/с [51].

При сделанных допущениях граничное условие приобретает вид:

аи

° U ( R , т ) = KU ( R , т ), д z

где K = ^eP w » 0,12 м ^{- 1}.

A m

Запишем задачу массопереноса при сделанных допущениях:

дU, , _пд ²u , ,

—^{( z , т} ) = B—T ^{( z} , t ), дт         д z

U ( z , т о ) = C о + C ₂ z ², аи

° U ( R , т ) = KU ( R , т ). д z

Система уравнений (18) представляет собой начально-краевую задачу третьего рода для уравнения теплопроводности, решение которой хорошо известно. Воспользуемся частным случаем этого решения при Bi ~ 1 или Bi >>  1.

U (z ,т) = D1 exp(-Бц 2т) cos ^x + D0, где D1, ц, D0 - константы, которые могут быть определены из начального и граничного условия.

Для проверки адекватности математической модели процесса микронизации зерна пшеницы сопоставим теперь функции влаго-содержания от времени, полученные из реше ния системы уравнений, с измеренными экспериментальными данными опыта.

Численное решение системы уравнений для периода убывающей скорости сушки осуществим с помощью математического пакета Maple 14, подставляя значения констант в систему (18). Сравнение результатов расчета с экспериментальными значениями приведено на рисунке 2.

Отразим данные в таблице 1.

Таблица 1

Расчетные и экспериментальные значения влагосодержания пшеницы

Вре мя, с	Uc (расчет), %	U c (экс-перим.), %	Абсолютная разница, %	Относит. погрешность, %
0	14,9	14,0	+ 0,9	6,42
15	13,5	13,5	0	0
30	12,2	12,2	0	0
45	10,8	11,3	-0,5	4,42
60	8,1	9,0	-0,9	10,0
75	6,0	7,0	-1,0	14,28
90	4,3	4,9	-0,6	12,24

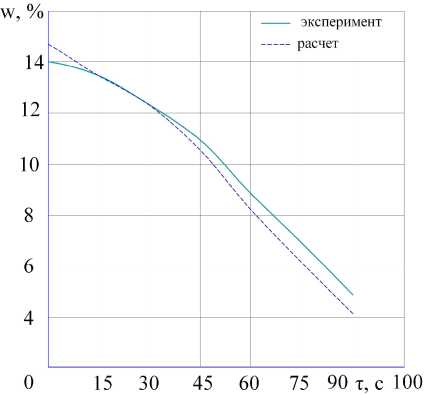
Рисунок 2. Сравнение расчетных и эксперимен- тальных данных изменения влагосодержания пшеницы от времени

Расчет средней относительной ошибки не превышает 7–10 % и показывает хорошее соответствие расчетных данных с экспериментальными значениями.