Математическое моделирование процесса прокалывания кожуры дыни

В настоящее время одним из важных направлений развития перерабатывающей промышленности Республики Казахстан является максимальное удовлетворение потребностей населения в качественных и безопасных продуктах с высокими пищевыми достоинствами на основе использования различных пищевых добавок растительного происхождения, а также нетрадиционных видов сырья и продуктов их переработки, в том числе с использованием бахчевых культур.

Бахчевые культуры, в частности дыня, являются богатым источником многих жизненно важных для организма человека пищевых веществ, прежде всего витаминов, углеводов и минеральных веществ.

Однако, как показывает анализ внутреннего рынка потребления плодоовощных консервов в республике, на прилавках магазинов практически отсутствует продукция переработки бахчевых культур отечественного производства. Одной из основных причин этого является то, что предприятия не заинтересованы перерабатывать бахчевые культуры, в частности, дыню, в связи с большой трудоемкостью процесса, обусловленной низкой его механизацией (отсутствием универсальных машин для очитки кожуры и резки).

Поэтому проблема механизации операций первичной переработки дыни является на сегодняшний день актуальной задачей.

Объекты и методы исследований

В качестве объекта исследования выбраны плоды дыни, знание механических свойств которых необходимо для разработки конструкции машины для снятия кожуры и нарезки на куски плодов дыни, обладающей малой энерго- и материалоемкостью, простотой конструкции и эксплуатации.

С целью создания методики расчета машины нами экспериментально был изучен процесс прокалывания кожуры дыни, так как этот процесс является малоизученным в отличие от процесса резки дыни [1,2] и лежит в основе конструкционных расчетов создаваемой машины.

Результаты и их обсуждение

Для установления влияния различных факторов на процесс прокалывания кожуры дыни использовали метод математического моделирования. При этом использовали ортогональное композиционное планирование эксперимента. Данный метод применяется с учетом результатов полного факторного эксперимента с последующим проведением опытов в дополнительных точках, соответствующих ортогональному плану (ортогональное планирование) [3].

В результате предварительных экспериментов установлено, что основными факторами, влияющими на процесс прокалывания, являются угол заточки рабочего инструмента (шипа) и диаметр шипа. Остальные факторы оказывают несущественное влияние на процесс прокалывания.

При исследовании влияния факторов были выбраны следующие пределы факторов: угол заточки рабочего инструмента (шипа) – 15 - 450, диаметр шипа – 2 - 4 мм.

Для составления матрицы ортогонального планирования определены факторы в натуральном масштабе:

• - для угла заточки рабочего органа:

_z0 = 15+45 = 30;     = 45-15 = 15;

1         2           ’     1          2’

• - для диаметра шипа:

О 4+2 , .4-2 .

z 0 =— = 3; Az_? =— = 1;

2      2            22

Для двухфакторного эксперимента уравнение регрессии имеет вид [4]:

У = b o + Ь 1 Х 1 + b 2 X 2 + Ь 12 Х 1 Х 2 + Ь^ + b 22 x | , (1)

где: b0 – свободный член, b1, b2 – линейные коэффициенты;

b 12 – коэффициенты парного взаимодействия;

b 11 , b 22 – квадратичные коэффициенты;

x 1 , x 2 – измеряемые и управляемые параметры.

Число опытов в данном случае рассчитывается по формуле:

N =N 0 +2k +n 0 ,          (2)

где: N 0 – число опытов полного факторного эксперимента 2k;

k- число факторов;

n 0 – количество опытов в центре плана.      представлена в таблице 1, матрица расчета

N = 9                                    коэффициентов регрессии – в таблице 2.

Матрица ортогонального планирования

Таблица 1 – Матрица ортогонального планирования эксперимента для различных угла заточки и диаметра шипа

Номер опыта	Факторы в натуральном масштабе		Факторы в безразмерной системе координат
	z 1	z 2	x 1	x 2	x 0
1	2	15	-1	-1	1
2	4	15	1	-1	1
3	2	45	-1	1	1
4	4	45	1	1	1
5	3	30	0	0	1
6	4	30	1	0	1
7	2	30	-1	0	1
8	3	45	0	1	1
9	3	15	0	-1	1
сумма			6	6	9

Таблица 2 - Матрица расчета коэффициентов регрессии (расширенная матрица ортогонального планирования)

№ опыта	x 0	x 1	x 2	(x i )2	(x 2 )2	x 1 x2	y
1	1	-1	-1	0,33	0,33	1	6,25
2	1	1	-1	0,33	0,33	-1	9,72
3	1	-1	1	0,33	0,33	-1	15,65
4	1	1	1	0,33	0,33	1	33,78
5	1	0	0	-0,67	-0,67	0	16,44
6	1	1	0	0,33	-0,67	0	21,67
7	1	-1	0	0,33	-0,67	0	10,58
8	1	0	1	-0,67	0,33	0	25,12
9	1	0	-1	-0,67	0,33	0	8,25
сумма	9	6	6	2	2	4	147,46

При этом значения коэффициентов (x , )2 и (x₂ )2 рассчитываем по формуле [5]:

(x i )2 = x 2 -^, (x ? )2 = x 2 -^ x l (3)

Рассчитаем линейные коэффициенты, квадратичные коэффициенты и коэффициенты парного взаимодействия [3].

. _2(x i y) , _2(x₂y) . _Ж)^{2 у)}    _2⁽х₂ ) ₂у)

Ь 1— , b 2—, b 11 --- , b 22 --- , b

ООО о

! 12 = ^Z(X1 ₄ ^X2y) , Ь 0 = ^(^хО ^ ^у) - 0,67 b11- 0,67b 22 (4)

Подставляя данные в выражение (4), получим:

b 1 = 6,02, b 2 = 8,39, b 11 = -0,57, b 22 = -0,01, b 12 = 3,67, b 0 = 16,38.

По результатам расчета получили урав- вания от угла заточки и диаметра шипа: нение регрессии зависимости силы прокалы-

Р =16,38+6,02(d-3)+8,39 (α –30)/15+3,67(d-3)( α –30)/15-0,57[(d-3)2 -0,67]-0,01{[( α -30)/15]2-0,67}, где: Р – сила прокалывания кожуры дыни, Н;

• α – угол заточки шипа, град.;

• d – диаметр шипа, мм.

На рисунке 1 изображена полученная поверхность, построенная на основе уравнения регрессии, на рисунках 2,3 – зависимости силы прокалывания кожуры дыни от угла заточки шипа и диаметра шипа, построенные по расчетным данным.

Сила прокалывания кожуры дыни определялась с помощью прибора Струк-турометр 1 [6]. Условия проведения опытов взяты в соответствии с таблицей 1.

Результаты приведены в таблице 3.

Сравнительный анализ данных (табл.3), полученных расчетным и экспериментальным путем, показывает, что расхождение составляет не более 5%, что приемлемо для инженерных расчетов.

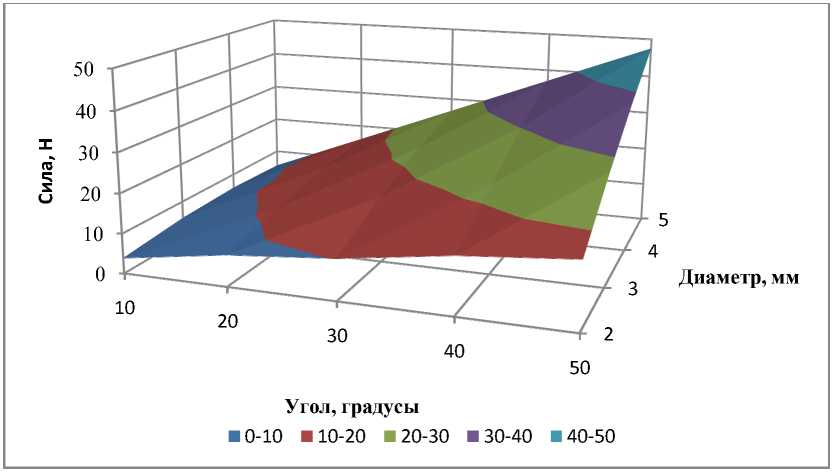
Рисунок 1 – Поверхность отклика зависимости силы прокалывания кожуры дыни от угла заточки и диаметра шипа.

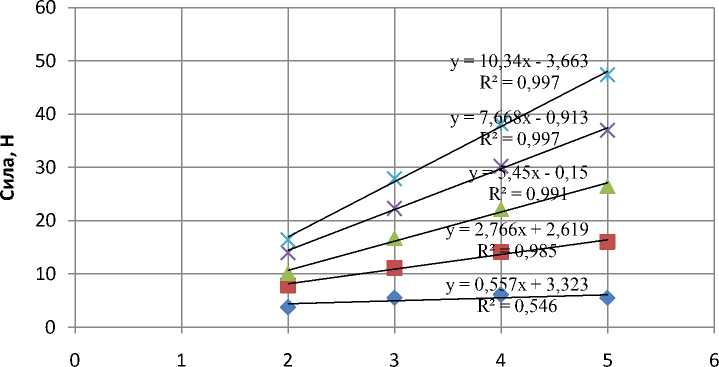
Диаметр, мм

♦ 10 ■ 20 ▲ 30 X 40 Ж 50

Рисунок 2 – Графики зависимости силы прокалывания кожуры дыни от диаметра шипа (расчетные данные) при различных углах заточки, град: 10,20,30,40,50.

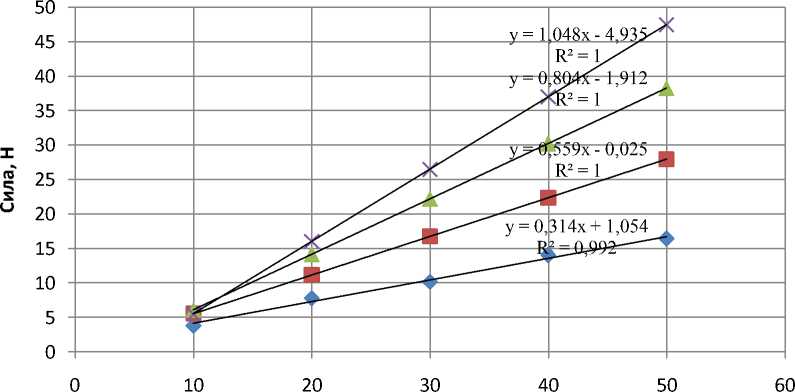
Угол, градусы

♦ 2 ВЗ А4 Х5

Рисунок 3 – Графики зависимости силы прокалывания кожуры дыни от угла заточки шипа (расчетные данные) при различных диаметрах, мм: 2,3,4,5.

Таблица 3 – Сравнительная оценка силы прокалывания кожуры дыни, полученной экспериментальным (у) и расчетным путем (ур)

№ опыта	Измеренное усилие прокалывания. Н	Расчетное усилие прокалывания. Н	Отклонение, %	Отклонение, %
1	6,25	5,75	0,5	8,0
2	9,72	10,15	0,43	4,4
3	15,65	14,89	0,76	4,8
4	33,78	34,27	0,49	1,4
5	16,44	16,77	0,33	2,0
6	21,67	22,22	0,55	2,5
7	10,58	10,18	0,4	3,8
8	25,12	25,15	0,03	0,1
9	8,25	8,37	0,12	1,5

Значимость полученных циентов проверяется при помощи Стьюдента по формуле [5]:

tj = 1511 Sbj коэффи-критерия

Полученные расчетные значения доверительного интервала оказались больше табличного значения, поэтому ни один из коэффициентов не исключается из уравнения регрессии.

Далее, используя критерий Фишера, проверили адекватность полученного уравнения регрессии по формуле[7]:

F=

s2

ост

S2 восп

где остаточная дисперсия рассчитывается по формуле:

S o²cm = Z ? (y i -yr i )2 / N — L, (7)

где L – число значимых коэффициентов в уравнении регрессии.

Так как расчетное значение критерия Фишера оказалось меньше табличного значения, то можно сделать вывод, что полученное уравнение регрессии адекватно описывает эксперимент.

Выводы и заключение

• 1.    Методом ортогонального композиционного планирования эксперимента была построена математическая модель процесса прокалывания кожуры дыни и получено уравнение регрессии, адекватно описывающее эксперимент.

• 2.    Сравнительный анализ данных силы прокалывания, полученных расчетным (методом математического моделирования) и экспериментальным путем, показывает, что расхождение между ними составляет не более 5%, что подтверждает достоверность полученных результатов.

Результаты проведенных исследований процесса прокалывания кожуры дыни легли в основу расчета конструкции устройства для очистки дыни от кожуры и ее резки на куски заданного размера. Опытный образец машины был изготовлен и апробирован в условиях ТОО «Плодоконсервный завод «Южный»».