Математическое моделирование процесса сушки снеков из фарша бычка азовского в псевдоожиженном слое

Для математического описания процесса сушки используют дифференциальные уравнения, которые с учетом принимаемых допущений не могут описать процесс с требуемой адекватностью [20]. Поэтому приходится прибегать к использованию моделей, описываемых дифференциальными уравнениями с разрывной правой частью [21].

Изучая влияние температуры на сушку кинетики средиземноморских мидий ( mytilus galloprovincilis ) в солнечной сушилке, работающей при принудительной конвекции, при трех температурах воздуха (50, 60 и 70 °С), была получена логарифмическая модель [19]:

MR = a exp (-kt) + c,(1)

где эмпирические коэффициенты рассчитывались по формулам:

а = 2.8293 - 0.06824^T + 6.54 10 4 T2(2)

к = 0.047 - 0.00155^T + 1.5 10 5-T2(3)

c = 2.6283 + 0.07502^T- 5.475 10 4T2(4)

Модель (1) показала высокую сходимость экспериментальных данных с коэффициентом корреляции ( r ) и самым низким значением пониженного хи-квадрата (х²), эффективное значение коэффициента диффузии D эф изменялось от 1.14 10^-9 до 3.61 10^-9 м²/с.

В работе [22] рассмотрен процесс сушки вторичных продуктов разделки рыб, в которой используется метод, базирующийся на основе уравнений тепло- и влагопереноса А.В. Лыкова. Используя разработанную компьютерную программу на языке Object Pascal в интегрированной среде программирования Borland Delphi 7, был смоделирован процесс сушки продуктов из рыбы путем решения задачи тепло- и влагопереноса на кубической сетке с учетом комбинированной технологии нагрева (конвективный и СВЧ-нагрев). Задаваясь теплофизическими и геометрические параметрами структуры частей рыбы и СВЧ-источника, получены графики и картограммы пространственного распределения влажности и температуры.

Морепродукты, подвергаемые тепловой обработке (сушки, обжарки и варки) имеют высокую влажность [1]. При этом внутренняя и внешняя тепло- и массопередача описывается уравнениями с граничными условиями третьего рода. Математическое моделирование, в этом случае, связано с переходом к многомерной модели с распределенными параметрами [2]. При этом теплофизические коэффициенты изменяются скачкообразно на движущемся фронте поверхности испарения. Решение сопряженных краевых задач тепло- и массопередачи с движущейся границей особенно важно для моделирования таких интенсивных процессов [3], как обжарка, сушка, в которых внутренний процесс контролируется сопротивлениями перемещения массы и теплоты, а внешние сопротивления играют существенную роль при обмене массы и теплоты с окружающей паровоздушной средой. Успешное моделирование этого процесса позволяет предсказать не только скорость обезвоживания продукта, но и распределение температурного поля в материалах пищи, что особенно важно, так как непосредственно влияет на ее качество [4]. Температурное распределение является весьма существенным во многих процессах сушки, например, таких как, сушка замораживанием [5-7], паром [8] и воздухом [9]. При сушке воздухом температурным распределением в материале, обычно пренебрегают, так как критерий Био мал из-за низкого коэффициента теплопередачи в воздушной среде. При этом представленные в литературе для воздушной сушки температурные распределения в пределах материала предсказывают изменение в его влагосодержании эмпирическим способом [10-12]. Однако, как было показано для модели сушки распылением единичной капли [13], температурное распределение внутри материала не может игнорироваться даже в этом идеальном случае. Решение краевой задачи с подвижной границей фазового перехода, определяемого температурой кипения воды при жарке или сушке перегретым паром, температурой сублимации при сушке замораживанием и температурой мокрого термометра в процессе воздушной сушки или сушки распылением позволяет обобщить эти процессы.

Цель работы - провести математическое моделирование анизотропного процесса получения сушеных рыбных продуктов для усовершенствования способа сушки в сушилках псевдоожиженного слоя с учетом восстановления динамики температурных полей и полей вла-госодержания на основе решения обратной задачи теплопроводности.

Материалы и методы

Объектом исследований является процесс сушки рыбного сырья на примере производства сушеных снеков из фарша бычка азовского (Neogobius melanostomus), представляющего собой сложный тепло массообменный процесс. Скорость его во многих случаях определяется скоростью внутри теплопереноса, определяющего условия испарения влаги в твердом теле. В случае высокоинтенсивных тепловых потоков, характерных для сушки рыбных продуктов в так называемом псевдоожиженном слое материала, когда под действием восходящего потока воздуха (сушильного агента) частицы слоя переходят во взвешенное состояние. Процесс в псевдоожиженном слое позволяет значительно увеличить поверхность контакта между частицами материала и сушильным агентом, интенсифицировать испарение влаги из материала и сократить продолжительность сушки. Применение в сушилках псевдоожиженном слоя, позволяет улучшить перемешивание материала и тем самым в несколько раз повысить величину коэффициентов тепло- и массообмена. Решение классической

задачи теплопроводности возможно с использованием критериев подобия, однако для анизотроп-

ных процессов их применение затруднительно. Для оценки параметров процессов тепло- и мас-сообмена предлагается использование метода математического моделирования, позволяющего идентифицировать коэффициенты тепло- и мас-сообмена, на основе решения обратной задачи нестационарного теплообмена при температурах выше 100ºС между поверхностью анизотропного тела и окружающей средой по закону Ньютона. Все процессы, связанные с переносом вещества,

на краевые задачи первого рода, когда критерий Био стремится к бесконечности. Следовательно, процесс нагрева кусочков из размороженного филе бычка азовского может быть описан краевой задачей нагревания тела при граничных условиях как первого, так и третьего рода, при последующей идентификации модели по критерию Био в эксперименте. Отчасти это положение наглядно подтверждается наличием общих точек пересечения изотермических линий (рисунок 1) иллюстрирующих задачу теплопроводности:

энергии и гидродинамические процессы описываются уравнениями Фика, Фурье и Ньютона [14]:

de qD dT ^"dF q'

где D – коэффициент диффузии; с – концентрация; x – координата; λ – коэффициент теплопроводности; η – коэффициент вязкости; V – скорость

T(x,y,z,0) = T o ,              (5)

-(VT)n + H(Tc-Tn) = 0(Tc>Tn),

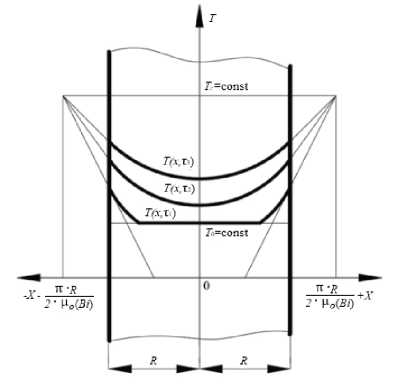
Рисунок 1. Распределение температуры в неограниченной пластине (симметричная задача)

Figure 1. Temperature distribution in an unbounded plate (symmetric problem)

движения потока.

Математическое моделирование нестационарного теплообмена для анизотропного тела в значительной степени затруднено из-за изменения теплофизических коэффициентов материала в процессе сушки. Предлагается для приближенного решения краевой задачи использовать метод Галёркина. Центральным элементом данного метода является весовая функция, выбираемая из семейства пробных поверочных и пробных функций из числа первых N функций некоторой полной системы, что является необходимым условием сходимости метода к точному решению при N → ∞ ( N – число слагаемых пробной функции).

В качестве исходного сырья для исследования процесса сушки рыбного сырья приняты кусочки из размороженного филе бычка азовского размером 10×7×5 мм, при равномерном начальном распределении температуры T o = const. В начальный момент времени продукт помещается в среду псевдоожиженного слоя с постоянной температурой T c >  T o . Теплообмен между поверхностью кубика и окружающей средой происходит по закону Ньютона. Это отображает в первом приближении конвективный теплообмен, который позволяет обобщить описание процесса

В декартовой системе координат уравнение теплопроводности (5) может быть преобразовано к дифференциальному уравнению по главным осям

теплопроводности анизотропных твердых тел

dT

d2T

d2T

d2T

dT & ^x dx² "*" ^^ dy² "*" ^^z dz²'

где a x a y , a z – главные коэффициенты темпера-

туропроводности анизотропного тела.

В общем случае, количество теплоты dQ , отдаваемое потоком сушильного агента продукту определяют по закону теплоотдачи Ньютона [15]:

dQ = adF(t1- t2)dT,

где α – коэффициент теплоотдачи; t 1 , t 2 – температура сушильного агента и продукта соответственно.

В свою очередь, конвективный теплообмен описывается уравнением Фурье [15]:

d£₊d£_y   dt_y   dt_y = _aV ² t'    (7)

dT dx x   dy y   dz z где Vx, Vy, Vz – скорости перемещения частицы в направлении осей соответственно x, y, z; ^2t -оператор Лапласа.

Уравнение трехмерного нестационарного процесса теплопроводности Фурье (6), может быть аппроксимировано граничными условиями первого рода, при изменении характерного размера, которые предполагают приравнивание уравнения Фурье в пограничном слое внутри продукта к уравнению Ньютона в пограничном слое снаружи у поверхности продукта [15]. Рассмотрим постановку задачи (2), с учетом дальнейшей суперпозиции частных решений, в одномерном варианте неограниченной пластины, толщина которой равна 2∙R , м (рисунок 1). При начальном равномерном распределении температуры известно аналитическое решение [16] задачи (6) для одномерной задачи, проиллюстрированной на плоскости (неограниченная пластина), в зависимости от ориентации продольного сечения продукта, на основе суперпозиции этих решение можно получить модель анизотропного переноса тепла при обосновании процесса производства морепродуктов:

Т(х, т, Тс, То,, Bi, RX = TO + (Тс- То) х

У /1   v00   Г___________2^siTi.[^in(Bi)]____________ n=0 llun(Bl)+sln[lun(Bl)]'COs[lun(Bl)]

cos[^_n ⁽ Bi ⁾ -|-]-e%p[-^_n ⁽ Bi ⁾² -^]})    (8)

где μ n ( Bi ) – корень характеристического уравнения аналитического решения (8); ctg[μ n ] = μ n /Bi ; Bi - критерий Био Bi = ^, характеризующий

A отношение интенсивности внешнего теплообмена к интенсивности внутреннего теплообмена; α – коэффициент теплообмена среды, Вт/(м²∙K); λ – коэффициент теплопроводности материала, Вт/(м∙K).

На рисунке 1 представлена известная графическая интерпретация теплообмена граничной задачи третьего рода [17], используя которую предлагается заменить характерный n^R размер ±R на ± 2  ^в^. Как видно из (3) темпера турные профили T(x, τ) для τ1<τ2<τ3 в неограниченной пластине имеют общие точки пересечения nR

(рисунок 1) с координатами ±----—-,ТС. Этот

2'^o(Bl)   с факт позволяет рассматривать данную краевую задачу с граничными условиями третьего рода как краевую задачу с граничными условиями первого рода при замене области существования решения от – R < x < R до области – ^•R           n^R

• < x <      . В этом случае возможно

2^0(Bl)        2^o(Bl)                J применение метода Галеркина для решения задачи нагревания анизотропного тела в условиях теплообмена по закону Ньютона. Приближенное решение ищется в области – n'R

n'R

- TT77 <  X <  7 TT77, 2-Ho(Bl)        2'Mo(Bl)’

позволяющей удовлетворить однородным граничным условиям, что является обычно практикуе- мым приемом при реализации традиционного метода Галёркина. В этом случае для реализации метода Галёркина необходимо иметь численную оценку границы этой области от варьируемых параметров числа Био и полуширины объекта по главной оси теплопроводности (рисунок 2).

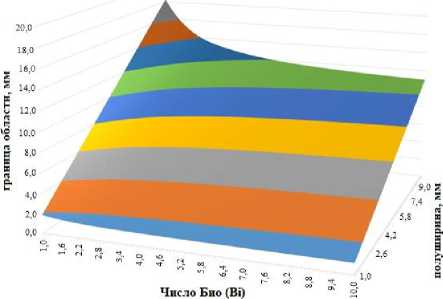
Рисунок 2. Двумерная сплайн интерполяция границы области существования решения от числа Био и полуширины объекта

Figure 2. Two-dimensional spline interpolation of the boundary of the domain of existence of the solution from the number of Bio and the half-width of the object

В этом методе предполагается, что неизвестная функция краевой задачи T (x, y, z, τ) уравнения теплообмена может быть представлена приближенным решением, образованным суммой элементов φ (x, y, z, τ, n) пробной функции, которые в данной работе представлены в следующем виде

Ф^у^п.) = bn- 1- P (  n^ -)•

2^o⁽BlxV _Qn 2

[l-p(^n^)  ]-[1-p(^^)  ]

[      \ 2^o(Biy)/Qnj  [      \2^o(BiZ)/Qn,J где n – текущий номер элемента пробной функции, n = 0, 1…, N; N – общее число слагаемых пробной n^R       n^R      n^R- функции;        ,        ,        – полугаба-

²^Uo^(Blx) ²^Цо(^В1у) ²^^o^(Blz)

риты длины ширины и высоты рабочей зоны теплового процесса, м; P – полиномиальная [функция, определяемая граничными условиями краевой задачи (1), первого рода на параллелепипеде области существования решения с габари-

^•R          n^R        n^R

™^{ми 2} 2^) ' ² 2^) ' 2^w7) ; ^{Q - Булева} матрица показателей степеней соответствующей полиномиальной функции (4); b n – весовые коэффициенты пробной функции.

Решение подобного рода задач возможно путем математического моделирования с использованием PTC MathCAD [18]. В качестве примера рассмотрим реализацию метода Галёр-кина для одномерного варианта краевой задачи (1) в среде инженерных расчетов PTC MathCAD. Для определения весовых коэффициентов пробной функции b n в начальный момент времени теплового процесса τ = 0 используем матричное соотношение B = M ^-1 ∙V , где элементы вектора V I и матрицы m i , j определяются следующими выражениями:

nR

2^0(Blx)

^V l     ^J _WR

п-R

2-^o⁽Bi_x^{) m}i,J ^- J n-R ^—^^^^^^^^^^^^^^^^^^^^^"

^P-oC^x)

" 2■Цo(Biж)

[1-( ^R- ) ]dx

2^o(Bix)

[1- ( x ) ⁱ ] • [1- (      '      ) I dx (11)

2Vo(BiX)                 2Vo(BiX)

Расчет элементов вектора (10) в среде инженерных расчетов PTC MathCAD для двухэлементной пробной функции может быть представлен в виде (здесь и далее расчетные формулы приведены в виде скрин-шотов решения поставленной задачи в среде PTC MathCAD):

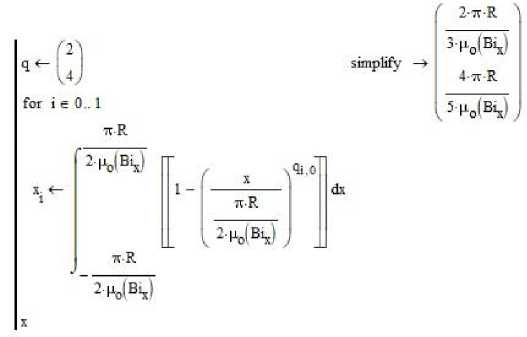
матрицы (12)

Расчет элементов в среде

PTC MathCAD для инженерных расчетов двухэлементной пробной функции может быть представлен в виде:

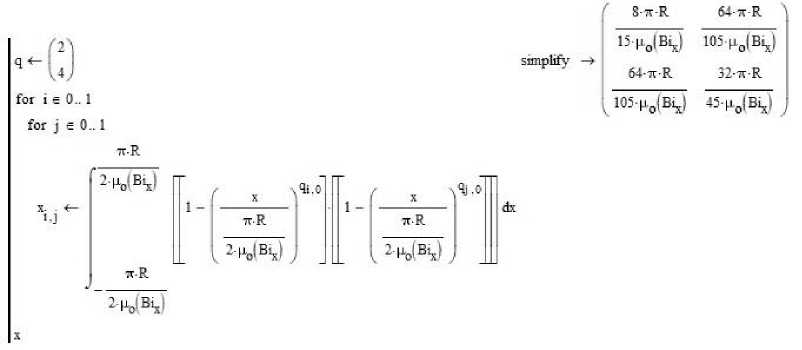
В этом случае весовые коэффициенты пробной функции b n в начальный момент времени теплового процесса τ = 0 определяются из (12) и (13) матричного соотношения B реализуемого следующим модулем

' 8-ir-R Ы-т-R y1

i^Mi ^i5bU

64-t-R     52-tR

^"i^By «-^[ву ,

В этом случае элементы матрицы переходного процесса D x определяются следующим выражением:

n-R di,j- S^^S3

2"^o(Bix) _

¹-⁽d ^x s=^

\ 2'^o(Bix)/

2-i!

•

3-р-о(ву

simplify

d2

з-^ву

Из (14) следует независимость весовых коэффициентов пробной функции b n от области – п-R            n-R

< x <      , позволяющей удовле-

2-Uo(Bi)          2-Uo(Bi)’ творить однородным граничным условиям.

dx2

1-(^^)

\ 2-^o(Bix)/

2-J1

dx,

Расчет элементов D x матрицы (15) в среде инженерных расчетов PTC MathCAD для двухэлементной пробной функции может быть представлен в виде:

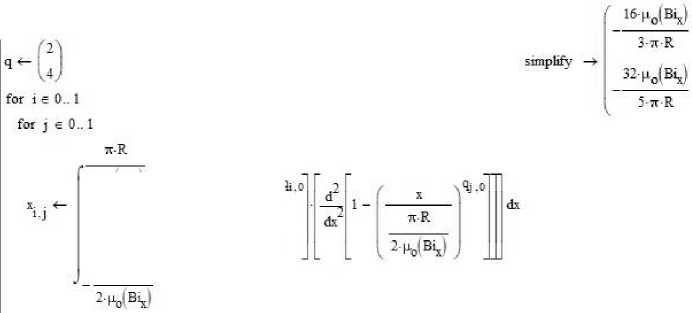
^МЧ) ' 5-tcR

«HoW

7xR

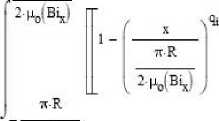
Используя элементы матрицы переходного процесса D определяемые соотношением (15) получаем систему обыкновенных дифференциальных уравнений, которая может быть решена численным методом, например, Эйлера реализуемым в виде матричной расчетной схемы

• У <^£> = у <£^-1> + [q. • _М ^-1 • _Dx • у <£^-1> ] • _Дт (17)

на шаге численного интегрирования системы обыкновенных дифференциальных уравнений, полученных из одномерной краевой задачи.

Используя соотношения (12), (13) и (16) первый шаг численного интегрирования по схеме (17) может быть представлен модулем:

где Yt> - столбец матрицы весовых коэффици- ентов временных проекций пробной функции

'_7

simplify

згг-^ дт ^(Bi,)2

x2R2

I^^ArpjB^r

2 „2

Остальные временные проекции могут быть получены аналогично (18) из итерационной формулы (17). В теории сушки используется метод анализа тепломассообмена, основанный на 1 совместном рассмотрении конвективнодиффузионного переноса паров влаги и температуры в потоке теплоносителя. В предлагаемой модели учет изменения влажности продукта связывается с изменением температуры рыбного сырья приняты кубики из размороженного филе бычка азовского размером 7x7x7 мм, что требует перехода от одномерной модели к её объемной реализации, учитывающей возможность использования аналитических зависимостей расчета элементов матрицы и векторов используемого и описанного выше одномерного метода Галеркина в среде инженерных расчетов PTC MathCAD. В этом случае использована весовая функция из двух квадратичных функций

Г x ² I

P ( x ) : = I   I второго и четвертого порядка:

I x У

Г

Ф ( x , Bi x , y , Bi y , z , Bi_z , n ) : =   1 - P 2 n

У (

z I

L ( Bi z ) )_Q

Q n ,0 У

•

1 - P I          I

² n I L ( Bi y ) к

X        ^Л У Qn ,1 У

• 1 - P ------

² n I L ( Bi x )

У

Qn ,2 у

,

где L( Bi x ), L( Bi y ), L( Bi z ) - полу габариты области существования решения по трем главным

осям теплопроводности, определяемые соотно-

шением

п-R 2-ц ₀ (51) ^-

В этом случае весовые коэффициенты при квадратичных функциях, задаваемых Булевой матрицей (20) принимают следующие значения:

Булева матрица показателей степеней этих квадратичных функций (19) имеет следующий вид:

b t = Г- 343

(   64

1029   3087

128     256

1029   3087

128     256

92611 (21)

512 )   ⁽    )

Г 0

Q T = 0

1   0   1   0   1   01

0 110 011

0  0  0   1   1   11

Матрицы переходного процесса, используемые для численного интегрирования краевой задачи (6) соответственно принимают следующий вид:

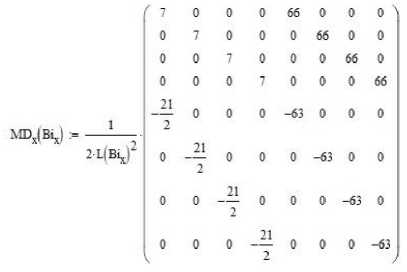
«W .

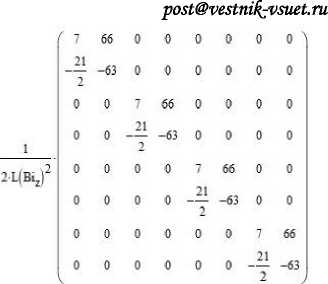
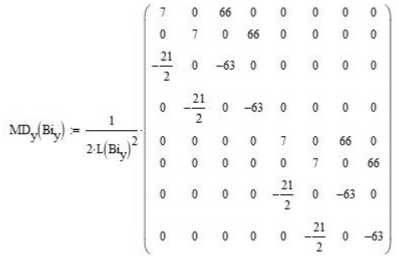
где MDx, MDy, MDz – матрицы переходного процесса по трем главным осям теплопроводности; Bix, Biy, Biz – числа Био по этим координатным осям.

Использование матрицы переходного процесса (16), (17) и (18) позволяет провести численное интегрирование весовых коэффициентов

Y^w : = B Y^ : = Y^{(t —1>} + [ a, • ( MD, ( Bi, ) • Y< t ^—1> ) + a„ • ( MD_y ( Bi_y ) • Y< t ^—1 ) + a_z • ( MD_z ( Bi_z ) • Y^{(t —1}' ) ] • At            (19)

Используемая итерационная схема численного интегрирования (19) позволяет получить решение задачи температурного поля (2) с приемлемой для инженерных расчетов точностью

T x , y , z , t ) = T o + ( T c - T o ) •

rows ( Q ) — 1

1 ^— S   t ⁽ Y ^W ) n ■ ^{Ф( X} ’ ^Bi x ’ У ’ Bi y ’ ^{Z ,} Bi z ^, n ) ]

n = 0

Используя выше изложенную расчетную схему краевой задачи (6) с граничными условиями третьего рода для моделирования предварительного прогрева влажного материала в процессе его тепловой обработки (20) до момента нагрева поверхности пластины выше температуры фазового перехода испарения влаги определили значения усредненной влажности в процессе испарительной сушки

RRR

( W_H —W_K)• J J J (Ф (Ю0 oC —Vt ( x,y,z , t ))) dxdydz

W =w +------—R—R — R-------------------- срт      к                             2-R ^2-R-2-R где wн, wк – начальное и конечное влагосодержа-ние материала в процессе испарительной сушки, Φ – функция Хевисайда.

Таким образом, использование интегрального показателя влагосодержания материала (21) позволяет идентифицировать параметры процесса испарительной сушки по изменению этого показателя во времени.

Результаты и обсуждение

В качестве исходного сырья для исследования процесса сушки рыбного сырья приняты кубики из размороженного филе бычка азовского размером 7×7×7 мм, характеризующегося следующими теплофизическими параметрами коэффициент теплопроводности a = 0,43 (Вт/(м∙K), удельная теплоемкость c = 3670 (Дж/(кг∙K) и плотность ρ = 930 кг/м3. В результате идентификации математической модели с использованием экспериментальных данных были получены следующие зависимости изменения влагосо-держания и температуры материала в процессе сушки (рисунок 3).

Использование расчетной схемы краевой задачи (6) с граничными условиями третьего рода для идентификации параметров модели процесса сушки основано на численном интегрировании с использованием матриц переходного процесса (16), (17) и (18), Учитывая полученные значения (22) коэффициентов температуропроводности с учетом геометрии объекта получаем возможность построить изменения влагосодер-жания в процессе испарительной сушки (рис. 3) от параметров идентификации модели – координатных чисел Био ( Bi x , Bi y , Bi z ) и коэффициентов температуропроводности ( a x , a y , a z ) входящих в пробную функцию температурного поля (20), формируемую векторами матрицы Y, определяемыми матрицами переходного процесса по трем главным осям теплопроводности (16), (17) и (18).

В качестве дополнительной зависимости, построенной по изменению влагосодержания продукта в процессе сушки средствами математического моделирования с использованием идентифици- рованных показателей (22) восстановлена зависимость изменения температуры материала от времени процесса (рисунок 3).

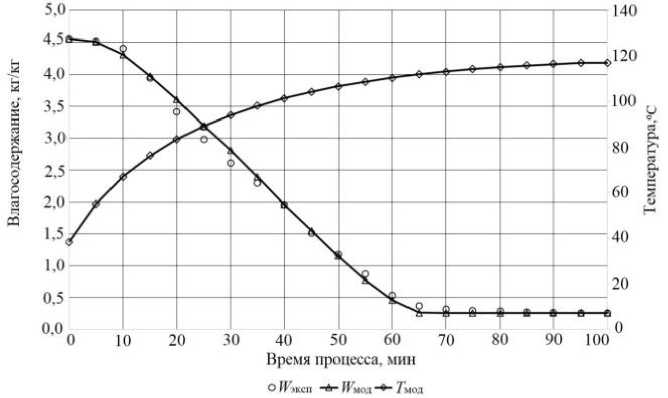
Рисунок 3. Идентификация модели по экспериментальным данным

Figure 3. Identification of the model based on experimental data

Результаты расчета по этим данным в среде инженерных расчетов PTC MathCAD коэффициента температуропроводности дают следующую усредненную оценку этих показателей:

Ito :-9J0—

Заключение

Установлено (рисунок 3), что при равномерном начальном распределении температуры в процессе предварительного прогрева температурная неоднородность возрастает вплоть до момента фазового перехода (100 °С) на поверхности высушиваемого объекта. Таким образом, уже предварительное моделирование показало важность учета фазы предварительного прогрева влажного материала, так как на этой стадии формируется температурный профиль, отличающийся значительной неоднородностью, что особо важно, так как температурная неоднородность непосредственно влияет на качество пищевого продукта. Подтверждена возможность учета анизотропии в процессах теплообмена при использовании объемной математической модели переноса с распределенными параметрами.

Предложенная математическая модель процесса сушки снеков из фарша бычка азовского в псевдоожиженном слое позволяет по гравиметрическим данным динамики среднего влагосодержания восстанавливать динамику прогрева высокобелкового продукта. Это является основой для понимания процессов термообработки на основе существующих концепций денатурации белковой составляющей морепродуктов. Использование этих восстановленных данных температуры и влажности в дальнейшем позволит оптимизировать технологические режимы термообработки пищевого сырья.