Математическое моделирование процесса теплопереноса в объеме замороженного продукта в условиях хранения в торговом холодильном оборудовании

Холодильное оборудование пищевой индустрии предназначено для кратковременного хранения скоропортящихся пищевых продуктов в торговых залах магазинов. Доброкачественность этих товаров обеспечивается пра- вильным хранением и соблюдением температурного режима. Шкаф-витрина холодильного торгового оборудования рассчитывается на требуемый режим при максимальных внешних и внутренних теплопритоках.

Если холодопроизводительность системы при данных условиях не соответствует действительным теплопритокам, это приводит к изменению заданной температуры. Недостаток холодопроизводительности не может быть компенсирован мерами регулирования. Избыток холодопроизводительности системы регулируется с помощью периодического выключения и включения компрессора. При этом температура в охлаждаемом объеме изменяется в зависимости от частоты открывания дверей [13].

В химической технологии широко распространены теплообменные и массообменные процессы со ступенчатым изменением потенциала среды. В теплообменных процессах в каждой секции аппарата (в разных периодах процесса) ступенчато изменяется температура, в диффузионных – концентрация вещества [421]. На экспериментальной модели была установлена зависимость температуры воздуха от продолжительности открывания дверей холодильных шкафов-витрин (рис.1). Шкаф загружали контрольными пакетами с термопарами. После загрузки шкаф работал до наступления установившегося режима. Работа оборудования продолжалась не менее 24 часов и включала не менее трех периодов оттаивания.

В соответствии с результатом эксперимента поставлена краевая задача теплопроводности в объеме замороженного продукта, представленного в виде неограниченной пластины. В шкафу-витрине требуется решить одномерное уравнение теплопроводности для однородного и изотропного тела дt (x, t)     5 2t ( x, t)

------= a -----—  ( t >  0, 0 <  x <  R )

дт        дx 2

(1) при равномерном начальном распределении температуры

t( x ,0) = t = const,                   (2)

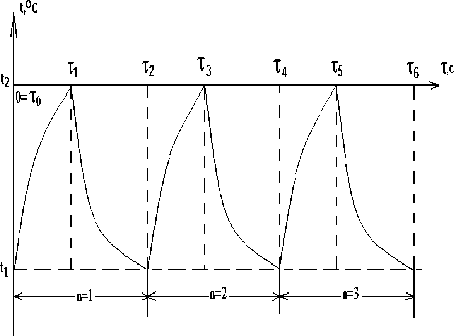
Рисунок 1 – Зависимость температуры воздуха от продолжительности открывания дверей холодильных шкафов

Решение симметричной задачи (1) – (4) является одновременно решением задачи нахождения температурного поля в неограниченной пластине толщиной R, когда одна поверхность ее имеет тепловую изоляцию (при х = 0 поток д< т) m тепла отсутствует, так как -------= 0), а про- дх тивоположная поверхность х = R поддерживается при температуре, описываемой условием (3).

Решение краевой задачи теплопроводности (1) – (4) получено методом интегрального преобразования Лапласа. Распределение температурного поля в продукте имеет следующий безразмерный вид:

T = £ A m + jj A n B n cos( _g n x ) e -^ц >« ₊ ... m = 1 ^{n m} n = 1

... +---- A ----,                                 (5)

Pd 2 Fo 2

где: A = 1 + Pd ₂ Fo 1 + e ^- Pd ^{2 Fo 2} - e ^- Pd ^{2 Fo} 1 -

e ^- Pd 2 ^{( Fo} 2 ^{- Fo} 1 )

дискретном граничном условии

- Pd ² (1 - e " Pd ^{1 Fo} 1 );

Pd ₁

^f l ^{( t )} = t 2 + ⁽ t 1 ^- t 2 ) e k^ ,

.    ( k 1 = const >  0);

t ⁽ R , ^{t )} = 1                                ,,    .

.f 2 ( t ) = t i + ( f , ( t i ) - t i ) e ^{- k} 2 ^{( t-T 1)} ,

( k 2 = const >  0)

и условии симметрии

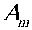
2 π mFo

= X 1 ^cos—-- Fo ₂

2 π mFo

+ x ₂ s^m------

²      Fo ₂

A n

= —(- 1) ^{n + 1 ц} n

туда;

B n

– начальная тепловая ампли-

n ц n =(2 n -1)-;                      (6)

= T 1

+

1 - _e ^-ц n Fo 2

^ T 2 e ^-ц n Fo ² (1 - e -^ц n Fo 1 ) - ... _v ... - T 1 (1 - e ^-ц n ^{( Fo 2 - Fo} 1 ) ) +

e

+ —

Ц 2_n^Fo 2

e ^Fo 1 ⁽ n n ^{— Pd} 1 )

—

e ^{— Pd} 2 ^Fo 1

—

.

.

.

Pd 2

2 ^V ... ^p n

—

e ^{— Pd} 2 ^{( Fo} 2 ^{— Fo} 1 ) + Ц n F^o 2

^; X 1 = ^p 1^{( a} 13 x^a13 ^{+ a} 24 x^a 24 ) ^{— Р} 2^{( a} 13 x^a 24 ^{— a} 24 x^a13Y ;

(

’ 24 x^a24) ^{+ P} 1⁽ a 13 x a 24

—

a 24 x a 13 ) ;

Р 1

. 2п mFo_A

= sin ¹

Fo ₂

1 _— e — ^Pd 1 Fo 1

1 + Г Pd 2 F0 2 ) ²

—

Pd 2 Fo 2

2п mFoj cos 1

Fo ₂

— Pd 2 Fo 2 1 1

— e V

—

Fol h

Fo 2 7

—

. 2пmFoA sin 1

л

—

V 2 nm 7

Fo 2

Р 2

—

e ^Pd 1 ^Fo 1

V

2πmFo sin 1

Fo ₂

+

PF 2 1

2 π m

V

—

e ^Pd 1 ^Fo 1 cos

2 π mFo ₁ Fo ₂

;

2п mFo    1 — e cos +

Fo ₂

—

.— Pd ! Fo 1

¹ ■                           ' I

V 2п m 7

1 +Г PdFo i ) ²

2п mro_A cos--------

Fo ₂

— Pd 2 Fo 2 1 1

— e V

Fo ₁

Fo ₂

+ Pd 2 Fo 2

. 2п mro_A sin—--- 1

—

V

Fo 2 I

7

(

1 — e ^{— Pd} 1 ^Fo 1

2 п mFo i Pd_AFoj . 2 п mFo> cos------- ¹ +-- ¹—² sin------- ¹

Fo ₂

Fo 2 )

.

Для сокращения записи новых формул введены следующие обозначения [21]:

m п

Fo ₂

^ a ; гиперболические тригонометри-

дель может быть рекомендована для инженерных расчетов и автоматизации качественного и безопасного хранения скоропортящихся продуктов в холодильном шкафу-витрине.

ческие функции, а также безразмерная координата заменены индексами: ch ^ 1; sh ^ 2;

cos ^ 3; sin ^ 4; X ^ x ; например:

ch

m^-X • cos V V Fo 2 7

V

----- > m^ X

N Fo 2 J

= ^a13 x ^;

sh

m п .

--sin

m п

Fo ₂

Fo ₂

= ^а 24 .

Выводы

1. На основании экспериментальных

ис-

следований поставлена и решена краевая задача теплопроводности, описывающая температурное поле в объеме замороженного продукта в условиях хранения его в торговом холодильном оборудовании – холодильном шкафу-витрине.

• 2.    Полученное аналитическое решение дает возможность определить темп охлаждения (нагрева), наименьший удельный расход энергии для поддержания необходимого режима, а также выбрать оптимальное соотношение продолжительностей периодов работы и отключения холодильной машины.

• 3.    После экспериментальной проверки и компьютерного исследования охлаждающего устройства разработанная математическая мо-

Обозначения:

1 ( x , т ) - температура, ^оС, K; t 1 - минимальная температура; t ₂ – максимальная температура; A t = t₂ — t 1 >  0 ; x - текущая координата; R -половина толщины пластины при симметричном теплообмене тела с окружающей средой; T - время, с; T o = 0 - время начала процесса; не уменьшая общности исследования проблемы рассматриваем одинаковыми длительности циклов (периодов) процесса "нагрев – охлаждение": [0, Т 2 ] = ^{[ т} 2 , ^т 4 ] = ... = ^{[ т} 2 _{( n —} 1) ^{— т} 2 n ^] = Ат = const , n e N ; N - множество натуральных чисел; a – коэффициент температуропроводности, м²/с; k ₁ k ₂ – коэффициенты скорости (нагрева, охлаждения), 1/c; k 1 >  k ₂ ;

f 1^{( т} 1 ) = ¹ 2 ^{+ (} t 1 ^{— 1} 2 ) ^e k 1 ^T 1

;

f 2^{( т} 2 ) ~ ¹ 1^;

£« 1 2

f ₁     при

^т 2( n — 1) < ^т< ^т 2 n — 1 ; f при ^т 2 n — 1 < ^т< ^т 2 n ;

¹ ( x , т )

t ₂

—

—

t ₁

t ₁

– безразмерная (от-

Б.А. Вороненко, И.Г. Кобылянский, О.А. Цуранов носительная) температура; T = —, i = 1,2; 1 ^t x                              a т

X = — - безразмерная координата; Fo = —;--

R                       R ²

число Фурье;) Fo = a^i- ( i = 1,2) ; ⁱ R ²

k i R ²

Pd i =---- - число Предводителева, — = 1, 2 .

a