Mathematical model of a wide class memory oscillators

In the paper of the Italian mathematician Vito Volterra [1], the notion of heredity (memory), a property of a dynamical system characterized by non locality in time, is introduced, which consists in the dependence of its current state on a finite number of previous states. V. Volterra investigated the hereditary oscillator - a vibration system with memory, which was written in the form of an integro-differential ecpiation with a difference kernel, a function of memory. Further, for such an oscillator, Volterra derived the law of total energy, in which an additional term appeared, responsible for the dissipation of energy in the vibrational system. This fact was confirmed in subsequent works.

In papers [2-9] fractal oscillators were considered, which represent the class of hereditary oscillators with a power-law function of memory. The peculiarity of such oscillators is that their mathematical description can be reduced to differential equations with non-local derivatives of fractional constant orders, which are investigated within the framework of the theory of fractional calculus [10].

In papers [2,4-7, 9] models of fractal linear oscillators were investigated in the sense of the Gerasimov - Caputo derivative, and in papers [3,8] - in the sense of the Riemann -Liouville derivative. Analytical solutions of model equations in terms of a special function of Mittag - Leffler type and generalized Wright-type function, oscillograms and phase trajectories are constructed. It is shown that in the regime of free oscillations, the presence of memory effects in the system leads to attenuation of oscillations as a result of energy dissipation, and with allowance for external periodic action, it is possible to stabilize the amplitude of the oscillations, with the phase trajectories reaching the limit cycle and also the resonance effect.

In a monograph by the Slovak mathematician I. Petras [3], the fractal nonlinear oscillator models whose differential equations contained fractional derivatives in the sense of Riemann - Liouville were considered and analyzed using numerical methods and considered the stability of the rest point of oscillatory systems. However, the stability and convergence of numerical methods have not been considered.

A further continuation of the investigation of hereditarity oscillators is associated with the introduction of the derivatives of fractional variable orders in the model equations. This is due to the fact that the orders of fractional derivatives are related to the properties of the medium in which this or that process takes place and changes with time under the influence of external influence. Therefore, papers [5-9] proposed the models of fractal nonlinear oscillators were proposed and investigated using explicit finite-difference schemes, whose equations contain both the derivatives of the constants, and variable fractional orders of the Gerasimov - Caputo and Riemann - Liouville types. With the help of computer experiments, the convergence of finite-difference schemes was shown and estimates of the computational accuracy of the method were obtained, oscillograms and phase trajectories were constructed. However, the cpiestions of stability and convergence were not formulated in the form of corresponding theorems.

From the analysis of the above publications on the study of hereditary oscillator, we can conclude that the main tool for their study is numerical methods, for example, finite-difference schemes. In most cases, the authors leave without attention the cpiestions of stability and convergence of finite-difference schemes, and even if they touch, then without formulating the corresponding theorems and proofs. Therefore, the goal of the present paper is to construct a finite-difference scheme for a wide class of hereditary (fractal) linear and nonlinear oscillators, and to prove its stability and convergence, formulate results in the form of corresponding theorems, and study finite-difference schemes on specific test examples.

1.    Formulation of the Problem

Consider the following model integro-differential equation for the function x ( t ) G C ³ (0 ,T ). where T> 0:

tt

У K i ( t - n ) x ( П ) dn + X J

K 2 ( t — n ) x ( n ) dn = f ( x ( t ) , t ) ,

where x ( t ) = d ² x / dt ² ,x( t ) = dx / dt, X >  0 - given const ant, functions K 1 ( t — n ) and K2 ( t — n ) ^_ difference kernels in equation (1) will be called memory functions, since they define the notion of heredity (memory) [1].

Ecpiation (1) describes a wide class of hereditary, depending on the form of the righthand side (function f ( x ( t ) ,t )) of linear or non-linear oscillators.

Definition 1. A nonlinear function f ( x ( t ) ,t ) on the right-hand side of equation (1) satisfies a Lipschitz condition with respect to a variable x ( t ).•

If ^{( x} 1 ⁽ t ) ,t ) ^{— f ( x} 2 ⁽ t ) ,t ) | < ^{L |x} 1 ⁽ t ) ^{— x} 2 ⁽ t ) | ,

L - Lipschitz constant.

Equation (1) describes a broad class of hereditary nonlinear oscillators, depending on the form of the function f ( x ( t ) , t ) on its right-hand side and the parameter X have the meaning of the coefficient of friction.

Remark 1. Note that the memory functions K 1 ( t — n ) and K 2 ( t — n ) can be chosen arbitrarily, depending on the conditions of the particular problem. We will choose these functions power-law, since power laws are often found in various fields of knowledge [11].

We choose the memory functions K1 ( t — n ) and K ₂ ( t — n ) in the form:

^{1 -e} ( * )                                     ^-Y ( * )

K 1 <  t — ’ ) =         K 2⁽ t — n > = та ’          ¹³¹

where y ( t ) , в ( t ) ^ C [0 T ], Г ( t ) - Euler-gamma function.

Taking into account relation (3) we obtain the following definition.

Definition 2. Derivatives of fractional variables of orders в ( t ) ^and Y ( t ) Gerasimov -Caputo type we call the follo wing operators of fractional differentiation:

tt gв(t)x ы =______1______ [ x(n) dn   9y(*)x , . =______1______ [ x (n) dn       „ d0*  x(n)    Г(2 — в (t ))J (t — n)в (t)-1   01 x (n)    Г(1 — Y (t ))J (t — n)’(*)'

0                                                        0

Remark 2. We note that in the case when the functions в ( t ) and Y ( t ) in the relations (4) are constants, we arrive at the definitions of the fractional derivative in the sense of Gerasimov - Caputo [12] and in the case when these constants в = 2 and y = 1 the operators of fractional differentiation (4) become classical derivatives of the second and first orders.

Taking into account Definition 2 the model equation (1) can be rewritten in a more compact form:

^d 0 *⁽* ) x ⁽ n ) + ^Xdo** ) x ⁽ n ) = ^{f (} x ⁽ t ) , t ) ■                               (5)

For equation (5), the initial conditions in the local formulation are valid:

x (0) = a ₀ ,x (0) = a 1 ,                                 (6)

where a ₀ and a 1 - given constants. As a result, we arrive at the Cauchy problem (5) and (6), which we will investigate.

• 2.    Explicit Finite-Difference Scheme

We construct an explicit finite-difference scheme for the Cauchy problem (5), (6). We divide the time interval [0 ,T ] in to N equal parts with a step т = T/N. We introduce the grid function x ( tk ) = xk, where tk = кт, k = 1 , ■ ■ ■, N — 1. The derivatives of the variables of fractional orders in equation (5) are approximated according to the relations in [12]:

k- 1

d$ * ) x ( n ) ^ Ak ^2 ajk ( xk-j +1 — 2 xk-j + xk-j- 1) ,                 G)

j =0

k - 1

дY( t) x (n) - Bk^ bjk (Xk—j+1 — Xk-j—1) ’ j=o where the weight coefficients have the form: aj,k = (j + 1)2 ek — j2 ek, bj^ = (j + 1)1 Yk —

J ^{1 -7}k. Ak

Y ( tk ) = Yk

τ - β_{k                λ}τ - γ_k

—- ttv , Bk =              Here to shorten the record: в ( tk ) = вк,

Г(3 — вк ) ^, k    2Г(2 — Yk )                                 k^V k ^,

Taking into account relations (7), the Cauchy problem (5), (6) in the difference formulation will have the form:

k - 1

k - 1

Ak $2 ajk ( x

k - j +1

-

² xk - j ⁺ xk - j - 1

) + B^ bj,k ( Xk - j +1

xk - j - 1)     fk,

j =o

j=o where x0 = a0,x 1 = a 1 + та0. Here to shorten the record fk = f (xk,tk). We write the problem (8) explicitly:

xk +1    A k + B k ⁽² Akxk   ( Ak   Bk ) xk - 1)

k-1

Ak +Bk E aj,k (xk-j+1 ~ 2xk-j + xk-j-1) ~ a +в  E bj,k (xk-j+1 — xk-j-1) + j=1

We note that the weight coefficients aj,_k and j have properties, which we formulate in the form of the following lemmas.

Lemma 1. For any k weights coefficients aj,kj^, as well as coefficients Ak,Bk have the following properties: k-1

к E aj,k = k2-вк, E bj,k = k1 -Yk, j=0

• 2)    1 = a o ,k > a 1 ,k > ... >  0 , 1 = b o ,k > b 1 ,k > ■■■ >  0 ,

3j Ak >  0 ,Bk >  0 .

Proof. The first property follows from the definition of weight coefficients. The second property is proved in the following way. We introduce two functions: ф ( x ) = ( x + 1)^{2 -e} k — x ^{2 в}^^к aiid n ( x ) = ( x + 1)^{1 Y}k ~ x ^{1 -Yk} П ( x ) = ( x +1)1 ^Y ~ x ^{1 -Y}- "'liwe x >  0. These functions are decreasing. Really derived from these functions:

ф' ( x ) = (2 — ek )  ( x + 1)^{1 в к} — x^{1 в к}   <  0 ,П ( x ) = (1 — Yk ) [( x + 1)^{1 Y k} — x ^{1 Y k} ] <  0 .

Therefore, the second property holds. The third property follows also the properties of the gamma function. The lemma is proved.

□

Let dOtt ) x ( n ) and dftt ) x ( n ) be the approximations of differential operators of Gerasimov - Kaputo type (7) for dOtt ) x ( n ) and be the д O tt ) x ( n ), Then we have the following lemma.

Lemma 2. Approximations d_ott ) x ( n ) a nd dOtt ) x ( n ) operators of the Gerasimov - Caputo type dы t ) x ( n ) a nd d^Y( t ) x ( n ) satisfy the following estimates:

^dSt t ) ^{x (} П ) ~ ^dot t ) ^{x (} П ) < ^C 1 т, ^dY(t ) x ⁽ n ) ~ ^tt ) ^{x (} П ) < ^C 2 т,            (10)

where C 1 at id C₂ - constants that are indcpendent of the parameter t.

Proof. Using the first property of Lemma 1 and Definition 2, we obtain:

_т 2 —в к

Г(3 - вк )

k- 1

£ ajkx ( t - jT ) + j =o

т ² —в к    k-1

^dot ^{x (} П ) = _r (3 _- ek ) Z0 ajk [ ^{x (} t ^- j^T ) ⁺ O ( ^т )]

2 -в к 2 -в к                 2 -в к     ^{k- 1}                        2 -в к

_{г(3 Л} O ^{( T 2)} = _{rf3 Л} ^ ajk^{x (} t ^- j^T ) + _rf3 O ■ ^{T 2)} =

Г (3 - ek)           Г (3 - вк) j =0                  Г (3 - ek)

_T 2 -в к

Г (3 - ek )

k- 1

^ aj,kx ( t - jT ) + O ( T ²) . j =o

Similar estimates can be obtained for the operator d$t ) x ( p ).

□ Proposition 1. According to Lemma 2, it can be shown that the explicit finite-difference scheme (9) has an error e = O ( т ). This fact will be used in computer experiments in determining the computational accuracy of the numerical method.

The finite-difference scheme (9) can be rewritten in matrix form

Xk +1 = MXk + Fk,                          (11)

Xk+1 = (x 1,x2, ...,xN-1)T, Xk = (x0,x 1, ...,xN-2)T, Fk = ( f0, f1, ..., fN-2)T, where the matrix M = (mij). i = 1, ...,N - 1 ,j = 1, ...,N - 1:

/

0 , j>i + 1 ,

mij =

^-Ai- 1 ( ^ai-j +1 ,i- 1

Ai- 1 ⁽2 ^{- a}i- 2 ,i- 1) ^- Bi- 1 bi- 2 ,i- 1 Ai- 1 ⁺ Bi- 1

j = i = 3 ,...,N - 1 ,

^{- 2} ai-j,i- 1 ⁺ ai-j- 1 ,i- 1) ^- Bi- 1⁽ bi-j +1 ,i- 1 Ai- 1 ⁺ Bi- 1

^- bi-j- 1 ,i- 1) ■ ,j

< i - 1 ,

2 A 1

m 1 , 1 = ¹ ,m 2 , 2 = A 1 + B 1 ,mi, 1 =

Bi- 1 bi- 2 ,i- 1 ^- Ai- 1 ^ai- 2 ,i- 1

Ai- 1 + Bi- 1

,i = 2 ,...,N - 1 ,

mi, 2 =

Ai- 1 ⁽² ai- 2 ,i- 1 ^- ai- 3 ,i- 1) ⁺ Bi- 1 bi- 3 ,i- 1 Ai- 1 ⁺ Bi- 1

.,N - 1 .

Theorem 1. An explicit finite-difference scheme (9) converges with the first order lx_k - x_k| = O ( т ) if the following condition is satisfied:

т < т ₀ = min

1 , \

2Г (2 - _Ъ- 1)

А Г (3 - ei- 1)

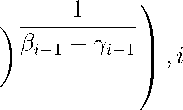
= 2 ,

.,N - 1 .

Proof. Let be X_k = ( x ₀ ,...,xN- ₂)^T the exact solution of system (8) and the error vector e_k +i = X_k +i - X_k +i ,e ₀ = 0 . . Then system (11), with allowance for Lemma 2, can be written as follows:

ek +1 = ^Mek ⁺ Fe,k ⁺ O ^{( т} ) ,

1                                                         T л п (I/(x 1 ,tk) - f(x1 ,tk)I ,•••, f(xk,tk) - f(xk,tk)I)       <

Ak + Bk

where.    Fe,k

w . D (L1 e 1, • • • , Lkek) — △ Fkek- △ Fk Ak + Bk that for anv k the ineqmditv holds lLk| < L (2).

k-1

||MH — max mi mp • According to Lemma i     j=1

1 _T

—-----— diag ( L 1, • • •, L_k ) . We note

Ak + Bk

Consider the norm for the matrix M:

1, we note that the inequality holds

HM li ra ^ 1- ^oW that foi’ the ^values °f ifo parameter A ^ 1 the iiomi |M|| _ю ^ 1.

however, the condition number p ^ 1 and is violated and the diagonal transformation is violated, therefore it is necessary to decrease the step t.

Further from equation (13), for any constant C >  0 independent of t, and the error rate, the following estimate holds:

ll ek +1 li ra <  II △ Fk + ^M ll ra ll ek li ra + C^T<  ^3 + Ak + Bk ^ ll ek li ra + C^T       Ufo

We introduce the notation in (14): s_k — ^3 +

following estimate:

L

Ak + Bk

)

s — Ct. Then we obtain the

ll ek +1 li ra < sk ll ek li ra + s < sk ( sk - 1 ll ek - 1 li ra + s ) + s ^—

• ^—    sksk - 1 || ek - 1 || _ra + ^{s (} sk + 1) < sksk - 1 ⁽ sk - 2 || ek - 2 || _ra + ^{s ) + s (} sk + 1) ^{— —} sksk - 1 sk - 2 || ek - 2 || _ra + ^{s (} sksk - 1 + sk + 1) <

  
  

< sksk - 1 sk - 2 ⁽ sk - 3 || ek - 3 || _ra + ^s ) + ^{s (} sksk - 1 + sk ^{+ 1) —}

• —    sksk - 1 sk - 2 sk - 3 || ^ek - 3 || _ra ^{+ s (} sksk - 1 sk - 2 ⁺ sksk - 1 ⁺ sk ⁺ 1) <

• <    sk sk - 1..... sk - r ll ek - r I I ⁺ s ⁽ sk sk - 1..... sk - r + 1 ⁺ • • • ⁺ sk ⁺ 1) •

Substituting into (15) r — k — 1. we obtain:

ll ek +1 || _ra < sk sk - 1 • ••• • s 1 li e 1 У + s ⁽ sk sk - 1 • ••• • s 2 + ••• + sk ^{+ 1)} < C о li e о У + O ^{( T} ) •

k

From the second initial condition (6) it follows: |e 1 1| < |e ₀ 1 | a nd C 0 — П sp.

p =1

Now according to our assumption Ai - 1 > Bi - 1, which leads us to the relation:

T <  (WW - WW) ^в‘ - ¹ — ^Y - ¹ ,i = ² ’-'^N — ¹ •           ™

У ^A i ^{(3 —} Pi - 1 )

The condition (16) begins to work at such values A , when a many of conditionality arises p ^ 1, and for sufficiently small values A , it suffices that the step satisfy the inequality т <  1. Therefore, we arrive at the relation (12). The theorem is proved.