Mathematical model of heating of plane porous heat exchanger of heat surface cooling system in the starting mode

The classical use of porous materials for the intensification of single-phase heatexchange processes [1] is greatly supplemented by new substantive applications, such as geothermal energy supply [2], technologies for obtaining structured polymeric materials [3], waste utilization in combustion in porous media [4], bioconvection in porous tissues of living organisms [5], etc. This recpiires consideration of transport phenomena in porous systems under nonstationary conditions [6].

The analysis of a. wide range of phenomenological mathematical models of nonstationary hydrothermal fields in porous media [7] showed that the representation of the fundamental Darcy-Brinkman-Forchheymer and Schumann ecpiations in the Hsu-Cheng form for the laminar flow regime of the Newtonian coolant [8]

V- v = 0 ,

P f Г ди    ( v • V ) v

ε ∂τ ε

-V p + P f V ² v -

^e ( Pc p ) f df; ^{+ vVt} f^ = ^V • ( ^xf • ^Vt f )

v pf k + pf

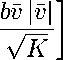
± ^a sf a sf ( t s    t f ) ,

(1 - ε ) ( ρc p ) _{s ∂τ} ^s = ∇ ( λ^s_e · ∇ t s ) ∓ α sf a sf ( t s - t f )

is the most convincing when interpreting experimental data and meets the criteria of qualitative and quantitative adequacy, where т is time; ( p,p,c_p ) f is density and dynamic viscosity of the liquid; e is porosity; ( p, c_p ) _s is density and heat capacity of the porous skeleton; v is a liquid velocity vector; g is a gravitational acceleration vector; p is pressure; K is a permeability of the medium; X^f, X ' are effective tensors of thermal conductivity coefficients of the liquid and the porous body skeleton material; t f , t s are temperature of the liquid and the skeleton of the porous body; a sf is a coefficient of heat transfer between the liquid phase and the skeleton of the porous body; a sf is a characteristic of surface area of the wetted surface in the porous medium.

For the first time the numerical analysis (1) - (4), under the assumption of homogeneity of the porous medium, constant thermophysical characteristics and local thermal equilibrium between the liquid phase and the porous skeleton, was given in [9] for the pulsational change in the liquid velocity at the entry to the porous layer with boundary thermal conditions of the second kind. The articles in [10, 11] are devoted to the experimental study of the settling of the temperature fields in porous media, in which the laws of the formation of the thermal initial region as a function of porosity were studied. However, the cpiestion related to the duration of the heating of the porous elements was not illuminated, in spite of the continuing interest in nonstationary processes in porous media [12].

1. Problem

We consider

Statement and Synthesis of the Model

a flat porous element in the 2 — D format in the Cartesian coordinate system with the origin at the edge of the lower bounding plane, which is heat-generating with the heat flux density q0. The longitudinal coordinate x is directed along the flow of the heat carrier (with known values of its velocity in the input section u0 = const and its temperature 10 = const), the transverse coordinate is perpendicular to the heat-generating plane. The porous medium is bounded by the heat-insulating surface located parallel to the heat-generating plane at the distance h (the surfaces bounding the porous medium are impenetrable for the coolant). Under the same assumptions as in [9], but refusing to simplify tf = ts, the system of equations (1)

- (4) in the dimensionless form can be written

as [13] + ∂V ∂Y = 0, (5) ∂U ∂X ∂U ∂U ∂U    ∂P ∂θ+U∂X+V∂Y = -∂X+ 1   ∂2U Re ∂X2 + d2 U ) ∂Y 2 -    1   + B √U2 + V2 U, Re · Da    Da (6) ∂V ∂V ∂V    ∂P ∂θ+U∂X+V∂Y =-∂Y+ 1   ∂2V Re ∂X2 + d2 V ) ∂Y2 -    1   + B √U2+V2 V, Re · Da    Da (7) 1 ∂Tf    ∂Tf    ∂Tf 1 ∂2Tf ∂2Tf     Nu p · Re ε ∂θ + ∂X + ∂Y = Pr · Pe ∂X2 + ∂Y2   + Pr·Re 2p (ΛTs -Tf) , (8) 2 (1-ε)Lu·Pr·Re∂∂Tθs=∂∂XT2s + ∂2Ts ∂Y2 - - Nu p-( iReep) (л T-—Tf) ■ (9) where e _ u0т/ (eh): X _ x/h Y _ y/h U _ u/u0: V _ v/u0: u. v are components of the liquid velocity vector v; P _ e2p/ (pfu0); B _ e2b b is the Forchheymers factor; Tf _ Xf (tf — tо) / (qоh); Ts _ X' (ts — to) / (qоh); Л _ Xf/AS; Re _ pfuоh/ (Tfe2) R Reynolds number: Re p _ pfu0dp/[6(1 — e) Tf] is pore Reynolds number: Da _ K/h2 Is Darcy number: Pr _ e (pep)f Tf j (Xfpf) Is Prandtl number: Nu p _ asfdp/Xf is pore Nusselt number; dp is a characteristic size of the extraporate space; Lu _ [Xf j (pep)f] j [X'/ (pep)s] is modified Lykov criterion characterizing the diffusion of heat in the liquid with respect to the diffusion of heat in the skeleton of a porous medium.

The hypothesis of a unidirectional flow of a coolant in the laminar regime [13], taking into account the fact that the diffusion of heat in the transverse direction of the porous layer is substantially greater than in the longitudinal one ( dT f s/ dY ² » dT fs/ dX ²)[14], allows to write the system (5) - (9) in the simplified form

1 dT f dT f _ eH ⁺ dX =

1    ^dT f

Re • Pr dY ²

Nu _D Re

⁺ ReN^{(л T} s ^{— T} f ) ’

⁽¹ - ^e )^LuRe • ^pr T ^_ dT

-

^Nu p (Ry)^{2 (л} T^— T f )

(П)

with the thermal boundary conditions corresponding to the formulation of the problem

T f ( X,Y, 0) _ T s ( X,Y, 0) _ 0 , dT f ( X, 0 , e ) _ dT s ( X, 0 , e ) _

∂Y

∂Y

1 ,

dT f ( X, 1 ,e ) _ dT s ( X, I ,e )

∂Y

∂Y

_ 0 .

When Da ^ 0, which corresponds to the maximum possible values of the heat transfer interphase [15], the liquid velocity profile in the porous layer is close to the ideal displacement regime, i.e. U ~ 1, which leads to the further simplification of system (10) -(14), since there is no need to solve the hydrodynamic problem.

The transition from the model with distributed parameters (10) - (14) to the model with lumped parameters is carried out according to the rule of geometric averaging

1 L

T'■• (e) _ L,/ TT<-‘ (X’Y’ e) dXd'Y’ where L _ l/h, l is a length of the porous heat exchanger. As a result, we obtain the Cauchy problem for the system of ordinary differential equations of the first order

- dTs de = (1

dT f       ε de _ PrRe	+ e      Л T . — Pr Re 2 p	L ε	Nu p ReA = + e PrRe p T f ’	(15)
1 —	Nu p Re	л T s	,      Nu p Re     л T (1 — e ) Lu Pr Re 2 p f,	(16)
e ) Lu Pr Re	(1 — e ) Lu Pr Re 2 p
	T . (0) _ T I (0)	_ 0 .		(17)

• 2.    Closing Relations

The classical physical model of porous media, as a rule, is presented in the form of dense packing of spheres [16], the voids of which are interconnected and completely filled with liquid, with only two phases: a liquid and a porous non-deformable skeleton. As the thermophysical parameters in (15) - (17) are homogeneous in space coordinates and do not depend on the temperature, they can be calculated from the relations [17]:

asf = 6(1 - e)/dp,(18)

asf = Xf [2 + 1, 1Pr0 (Pfu0dp/Pf)0’6] /dp,(19)

where Pr⁰ = p f c_p f / Xf, X f is heat conductivity of the liquid;

Xf = [e + (0, 1 ^ 0, 5) Pr01 /3 (pf uоdp/pf)] Xf,(20)

XS = (1 - e) Xs,(21)

where X_s is heat conductivity of the skeleton of the porous medium: d p is number average diameter of spherical particles in the porous layer. The dimensionless parameters in (15) - (17) on the basis of (18) - (21) can be defined as follows: Re = Re ⁰ /e 2. Re p = Re P / [6(1 - e )]. Pr = e Pr⁰ / ( e + 0 , 3Pr⁰ Re P ). Nu p = (2 + 1 , 1Pr^{0 /} 3Re 3/5 ) / ( e + 0 , 3Pr⁰Re p ), where Re ⁰ = p f u 0 h / p f, Re 0 = p f u 0 d p / p f.

• 3.    Solutions

The change in the temperatures of the coolant and the skeleton of the porous medium from the dimensionless time is obtained by means of the one-sided integral Laplace transform [18]

[ y Л B + e ( L^{- 1} + B )]² <  4 ey Л B ( L^{- 1} + 2 B ) ,

1 ( a + y Л B ) + — ^ 1        / ax • ( a            —

^T f ^{( 6 )= eA} —       .         ^exp( a® ^)sin r^+arctg e+ykb

-

arctg — ) a

+

+ YЛB 2 } + EYЛAB  1 ( 2 1 2 )  eXP (a®) sln (—® - arctg —) + 2 1

a2 + —2             — a2 + —2                          a a2+

^T s ^{( 6} ) = YA { ^[ a ⁺ " ⁽ ^Н^ ⁺ " } ^eXP ⁽ a® ) ^sln ( ^{—6 + arc}tg a + ₆ ( L - 1 + B ) ^{- arc}tg " ) ⁺

+ E (L i + B) ^ + EYAB  1 ( 2 I 2 )  eXP(a®)sln (—® - arctg —) ■ 2 1

a2 + —2             — a2 + —2                          a a2+ when [YЛB + e (L-1 + B)]2 = 4eyЛB (L-1 + 2B),

Tf (6) = 2!2ЛгВ {! + [-1 + 80 (! + 2siB) »] exp (s06)} , Ts (®) = ^lAIL^ {1 + [-1 + s 0 (1 + ^(L-s+B)) ®] exp (s 0 ®)} , when

^[ Y Л B + e L- ¹ + B )] 2 >  4 ey Л B L- ¹ + 2 B ) ,               (22)

= ™  2 ey Л AB eAs 1 + 2 ey Л AB         eAs 2 + 2 ey Л AB

T f ( 6 ) =-- 1--7-------7 exp( s 1 6 ) +--7-------7 exp( s 2 6 ) ,    ^

s 1 s 2            s 1 ( s 1 - s 2 )                         s 2 ( s 2 - s 1 )

T (AX ^{2 EY}A ⁽ L ^{1 + 2} B ) -u ^YAs 1 ^{+ EY}A ⁽ L— ^{1 + 2} B )

^T s ^{( 6} ) =------ 7 7 7 2------ ⁺------ T Tc s T — s 2)------ ^{exp ( s 1 6} ’⁺

YAs2 + eya (L 1 + 2B) +---------..          ..=xp

s 1 — s о + s 0 — 4 ey Л B ( L ¹ + 2 B ) , s 2 — s 0 — s 0 — 4 ey Л B ( L ¹ + 2 B ) .

• 4.    Computing Experiment

  Let’s consider the real situation. Let the porous layer consists of dense packing of identical copper ball elements with the diameter d p = 0 , 5 ■ 10 ^- 3m, and e = 0 , 4; h = 0 , 01m; l = 0 , 02m. Thermophysical characteristics 0f the coolant are close to water, then p f = 1000 kg 1113: p_s = 2700 kg m³: p f = 5 ■ 10 ^{- 4} Pа - s: c_p f = 4190 J (kg - K): c_ps = 880J (kg - K): X f = 0 , 68 W/(m - K); A s = 211 W/(m - K). The values of the determining parameters are given in Table.

Table

Re о	Pr	Re p	Re	Lu	Л	Nu p
20	0,930	0,278	125	0,004	0,007	2,719
100	0,245	1,389	625	0,015	0,027	1,235
200	0,128	2,778	1250	0,029	0,052	0,868

The dimensionless form of recording the equations of the mathematical model allows to abstract from the specific value of the heat flux released by the cooled heat-stressed surface. The results of the calculations show (Fig. 1) that with an increase in the Reynolds number, the dimensionless time of establishment of the stationary regime increases. However, in denominate quantity, it decreases, as value u ₀ grows faster than 6. This means that a larger flow of the coolant through a porous element leads to an early onset of a stationary regime, which is consistent with physical concepts of heat transfer in porous media.

The local maximum of the temperature of the porous skeleton is explained by the fact that the coolant is present in the region adjacent to the inlet for some time. At the same time, the heat comes from the heat-generating surface by the mechanism of thermal conductivity into the skeleton itself, which is still free from the coolant, which causes the increase in its temperature. With the complete passage of the coolant through the porous element, the temperature of the skeleton decreases and approaches the stationary value. For the coolant temperature, there is no such a regularity. Thus, the proposed model makes it possible to answer the question of the impossibility of the impact of overheating

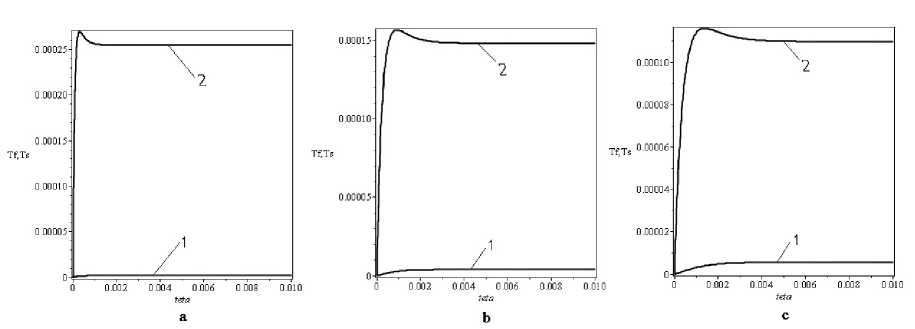
Fig. 1. Dynamics of the temperatures of the coolant and the porous heat-exchange element when the heat-stressed surface is cooled for different Reynolds numbers of the inlet coolant flow: a — 20; I) 2: c 5:1 Tf 2 ^— T s

of the porous skeleton in the starting condition on the creation of the conditions for the phase transition in the coolant.

The increase in porosity (Fig. 2) leads to the increase in the dimensionless and real transition time, since in this case, the Reynolds number for the interskeleton space decreases and in addition the transition temperature naturally increases.

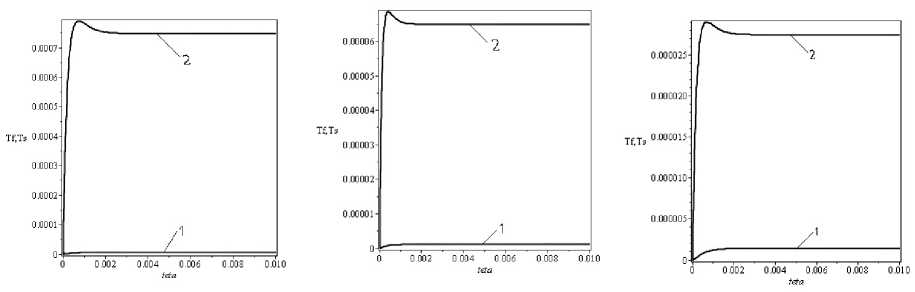
Fig. 2. Dynamics of the temperatures of the coolant and the porous heat exchange element at

Re 0 = 20 aiid e = 0 , 5: 1

T f : 2 T s

Fig. 3. Dynamics of the temperatures of the coolant and the porous heat exchange element at Re 0   =   200 and dp = 3 • 10-5: 1 - Tf. 2 -T s

Fig. 4. Dynamics of the temperatures of the coolant and the porous heat exchange element at Re 0 = 200 and h = 0 , 02 m: Y-TfT - T₈

Reducing the dispersion of the particles in the porous element shortens the transition time and reduces the temperature of the coolant and the porous skeleton by increasing the surface area of the heat transfer (Fig. 3).

The increase in the thickness of the porous layer leads to the decrease in the temperature of the coolant and the porous skeleton with the reduction in the transition time (Fig. 4).

Since, for the vast majority of practically important cases, condition (22) is satisfied and s 1 is substantial!у smaller than s 2, then, for example, from (24) we can find an approximate estimate of the dimensionless time for setting the stationary cooling regime from                        _ _

TS (6c) /T (x.) - 1 = 6, from where

6c ^ — In s1

Г 2 6 (s i - s 2) y Л B s 2 ( s 1 + 2 YЛ B )   ’

where 6 is predetermined relative accuracy of determination 6_c (usttally 6 = 0 , 01).

Proceeding from the assumption that the thermal initial section in the flat porous layer in the hydrodynamic regime of the ideal displacement of the coolant with constant velocity is formed in time similarly to the heat transfer coefficient along the axial coordinate, comparison with the experimental data from [19] (Fig. 5) shows a satisfactory correlation with the calculation results according to the proposed formula (25).

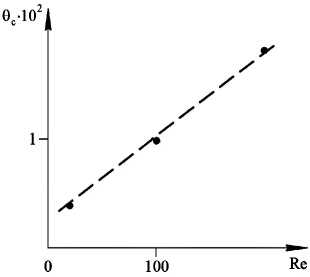
Fig. 5. Dependence of the determination of the dimesionless time on the Reynolds number for the coolant:---is empirical approximation [19]; • is calculation by (25)

Conclusion

The proposed model makes it possible to identify the duration of the transient thermal regime when cooling heat-stressed surface with a porous heat exchanger without complicated calculations and to not only select the rational macro- and micro-geometry of the porous skeleton, but also to evaluate the effect of thermophysical characteristics on the kinetics of the setting of the thermal stationary regime.