Матричные уравнения движения систем твердых тел в гамильтоновых переменных. Системы c замкнутыми цепями
Автор: Иванов В.Н.
Журнал: Вестник Пермского университета. Математика. Механика. Информатика @vestnik-psu-mmi
Рубрика: Механика. Математическое моделирование
Статья в выпуске: 4 (47), 2019 года.
Бесплатный доступ
Работа посвящена разработке методов компьютерного моделирования динамики систем твердых тел с замкнутыми кинематическими цепями. Рассмотрен случай голономных связей. Представлена новая матричная форма уравнений движения в гамильтоновых переменных. Особенность системы уравнений состоит в том, что она разрешена относительно производных обобщенных импульсов и не содержит реакций связей. Получены рекуррентные формулы для определения всех кинематических и динамических переменных, входящих в уравнения. На примере одной механической системы продемонстрированы все этапы подготовки первичной информации для составления уравнений движения в предлагаемой форме.
Система абсолютно твердых тел, уравнения движения, динамика, математическое моделирование, обобщенные координаты, импульсы пуассона, матрично-геометрический метод
Короткий адрес: https://sciup.org/147245460
IDR: 147245460 | УДК: 531.01+004.94 | DOI: 10.17072/1993-0550-2017-4-13-20
Текст научной статьи Матричные уравнения движения систем твердых тел в гамильтоновых переменных. Системы c замкнутыми цепями
В статье выводится новая матричная форма уравнений движения систем связанных твердых тел (СТТ), имеющих в своей структуре замкнутые кинематические цепи с использованием квазискоростей, обобщенных координат и обобщенных импульсов (импульсов Пуассона). Уравнения предназначены для компьютерного моделирования динамики СТТ.
Работа является продолжением исследования [1], в котором аналогичные уравнения выведены для СТТ со структурой дерева и показана их взаимосвязь с классическими уравнениями движения механических систем.
1. Описание механической системы
Структуру любой системы абсолютно твердых тел можно представить в виде графа, вершины которого есть тела системы, а ребра – шарниры. Этот граф назовем первичным графом.
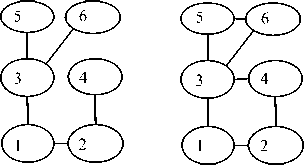
Если путь между любыми двумя вершинами определяется единственным образом, то говорят, что граф системы имеет структуру дерева (рис. 1, а). Если существуют два различных пути между какими-либо двумя вершинами, то в системе присутствуют замкнутые цепи (рис. 1, б).
а) б)
Рис. 1. Примеры СТТ: а) со структурой дерева, k = { 0,1,1,2,3,3 } ; б) с замкнутыми цепями
В СТТ со структурой дерева можно пронумеровать тела и шарниры таким образом, чтобы для любого тела или шарнира в графе системы номер предшествующего ему тела или шарнира был меньше.
В этом случае для полного описания структуры взаимосвязей тел в системе достаточно одного целочисленного массива k = { k ,..., kN } , на i -м месте которого расположен индекс тела или шарнира, предшествующего i -му.
В случае СТТ с замкнутыми цепями первичный граф всегда можно превратить в граф со структурой дерева (вторичный граф) путем размыкания замкнутых контуров. Размыкание проведем с помощью раздвоения в каждом замкнутом контуре одной из вершин первичного графа. При этом одну и ту же вершину можно раздваивать произвольное число раз. При раздвоении все образы одной вершины остаются не связанными непосредственно между собой и принадлежат к различным ветвям вторичного графа. Во вторичном графе существует соответствие между образом и прообразом раздвоенной вершины. Соединим пунктирными ребрами все такие пары вершин вторичного графа (рис. 2).
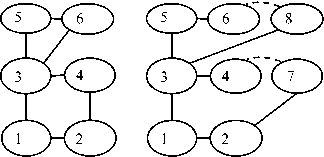
k = { 0,1,1,3,3,5,2,3 }
а) б)
Рис. 2. Пример СТТ с замкнутыми цепями: а) первичный граф; б) вторичный граф
Массово-инерционные характеристики раздвоенных вершин первичного графа и действующие внешние силы произвольным образом распределим между образами и прообразами вершин вторичного графа.
Пронумеруем тела и шарниры вторичного графа в соответствии с введенной выше правильной нумерацией вершин СТТ со структурой дерева.
Пусть N - число вершин вторичного графа. C каждым i-м телом свяжем множества: P' - упорядоченное множество индексов шарниров, составляющих путь между нулевым и i-м телами; U- - множество индексов шарниров, для которых i-е тело является предшествующим.
Массивы k ,
{ Pi \ { Ui }
характеризуют
структуру вторичного графа.
-
2. Уравнения движения СТТ
с замкнутыми цепями в гамильтоновых переменных
В статье [1] были выведены уравнения движения СТТ со структурой дерева в следующей матричной форме:
Mv - ST ц = 0,
-
- SSv + Aq = - v r , (1)
AT P = P, p = ( AT - ATq) p + Q, (2)
где
M = diag ( M 1 ,..., M n ) , M i =
[ m i E. I miri
c
- mi r i
J i J
F = col ( Fi,..., Fn ), Fi= col (fO, mo ), v = col (vi,..., Vn ), Q = col (Qi,..., Qn ) = AT TTF, nt - масса i-го тела; J - тензор инерции i-го тела; rc - радиус-вектор центра масс i-го тела в связанной с ним системе координат (СК); f o, mio - главный вектор и главный момент активных сил, действующих на i-е тело, заданные в i -й СК; Q - матрица-столбец обобщенных сил. Здесь S = ( Sij) - матрица кинематической структуры:
E 6 , j = i, _
S ij =-- C i , j = k i , i , j = 1, N ,
0 6 x 6 , j * 1 V k i ,
C = ^ G - G Pl^ - матрицы, определяющие переносные движения, матрицы A = diag ( A{ ,..., AN ) и v r = col ( v r ,...,v r ) задают относительные движения тел системы. В этих матрицах: P = Pi ( Qi, t ) - матрица-столбец координат начала СК, связанной с i -м телом, в k. -й СК; G = G ( q. , t ) - матрица, столбцами которой являются координаты единичных базисных векторов k -й СК в i -й СК (матрица преобразования координат из k -й в i -ю СК);
I U I
Vi = i , Vi =
1 iJ
и
a i1
a * i
и dPj r _ с dpi a- = G- —r, и = G.---, a.-.-
1j l dq i dt lJ1
ain a" j dGT
,
d q ’
m i = Gi
d G T d t
J = i, ni ;
Введем матрицу s =
число строк
u i , m — матрицы-столбцы проекций абсолютных линейной и угловой скоростей тел механической системы на оси i -й СК;
Q i =f m i 0 1 , Q = diag ( Q i ,..., Q n ) .
UJ:
Волнистой линией над символом обозначена кососимметрическая матрица векторного nT произведения. Наконец, q{ = (q!,...,qp I - векторы (матрицы-столбцы) обобщенных координат, параметризующих уравнения связей i-го шарнира, n - число обобщенных координат, q = col (q},..., qN) - вектор всех обоб
которой соответствует числу дополнительных замкнутых циклов, а число столбцов совпадает с числом вершин (тел) во вторичном графе системы. Пусть s. = 1, если j - номер вершины в первичном графе системы, принадлежащей i -му замкнутому циклу, s = -1, если j - номер ij вершины во вторичном графе системы, являющейся образом соответствующей вершины первичного графа и принадлежащей i-му замкнутому циклу, s = 0 во всех других случа-ij ях. Для системы тел, изображенной на рис. 2,
щенных координат системы.
Особенность уравнений (1), (2) состоит в том, что они выписаны относительно расширенного множества гамильтоновых переменных: { q , p } - обобщенных координат и импульсов и { г , ^ } - декартовых скоростей и импульсов (множителей Лагранжа).
Как было отмечено в [1], введение в уравнения движения дополнительных переменных оправдано при компьютерном моделировании динамики СТТ.
Входящие в уравнения (1) кинематические соотношения - Sv + Aq = - vr можно записать в виде явных выражений
v = T (Aq + vr) = Bq + р,
матрица s имеет вид f 000 1 00 -1 0
s =
^ 0000 1 00 - 1
Будем считать, что СК, связанные с образами и прообразами раздвоенных вершин, расположены в телах одинаково. Тогда абсо-
лютные координаты и скорости всех точек прообразов и образов раздвоенных вершин в абсолютной СК должны совпадать. Это озна-
чает, что условия замкнутости кинематических цепей накладывают на движения вершин вторичного графа следующие кинематические и геометрические связи (ограничения):
sGTv = sGTa (Bq + р) = 0, (3) sn = s j G^vd т = 0, (4)
где G a = diag ( G a ,..., G N ) - матрица преобра-
где B = TA - матрица касательного локального базиса пространства возможных перемещений всех тел системы; (р = Tvr - вектор явно зависящих от времени компонент вектора скоростей v ; обратная к S матрица T = S -1 является блочной 6 N хб N -матрицей, подматрицы которой могут быть вычислены без обращения матрицы S по рекуррентным формулам [1]:
зования шестимерных абсолютных координат (линейных и угловых) всех тел системы в связанные с ними СК;
G =
G 0 0
0 G 0 ,
, G 0 = GG k .
Ограничения (3), (4), очевидно, являют-
Т- = ij
Е б , CT k i , J ’ 0 б x б ’
j =1 ’ ____ j е P ’ 1 ’ j =1’ N. J £ Pi ’
ся зависимыми, поэтому при выводе уравнений движения будем учитывать только кинематические связи (3). Соотношения (3) говорят о том, что часть вариаций обобщенных координат S q являются линейно зависимыми
Перейдем теперь к описанию того, каким образом в уравнениях (1), (2) можно учесть дополнительные голономные кинематические связи, появляющиеся в результате замыкания вторичного графа СТТ.
и удовлетворяют системе уравнений s G ^ B S q = 0. (5)
Модифицируем уравнения движения
(1), (2), используя принцип Гамильтона-
Остроградского. В [1] показано, что для СТТ со структурой дерева вариацию действия по Гамильтону 5 H можно привести к виду
t
S H = J 8 vT ( Mv - S T / + 8// ( Aq + v r - t
- S v ) + 8 qT ( Q - p + A T - A T q ) dt = 0, если кинематические связи учесть с помощью множителей Лагранжа и и ввести переменные p = AT / .
При выводе уравнений движения СТТ с замкнутыми цепями мы не будем выражать зависимые вариации 8 q через независимые из соотношений (5), а учтем последние с помощью множителей Лагранжа П • Тогда после несложных преобразований получаем следующее равенство:
8 H = J 8 vT ( Mv - S T / ) + 8/ ( Aq + v r - Sv ) + t 1
+8 qT ( Q - p + ( A T - AT Q ) / + BT Ga£ T p ) dt = 0. Коэффициенты перед вариациями множителей Лагранжа 8/ равны нулю, так как являются кинематическими уравнениями, коэффициенты перед вариациями декартовых скоростей S v обнуляются выбором множителей Лагранжа (декартовых импульсов) / , так как их число совпадает с числом соответствующих коэффициентов. Таким образом, получаем группу кинематических уравнений (1). Часть коэффициентов перед вариациями обобщенных координат 8 q можно обнулить выбором множителей П , число которых совпадает с количеством уравнений связей (5). Оставшиеся вариации 8 q являются линейно независимыми, поэтому вариация 8 H будет равна нулю тогда, когда каждый коэффициент перед 8 q будет равен нулю. Следовательно, для СТТ с замкнутыми цепями группа динамических уравнений (2) преобразуется к виду p = d ( A T / ) = ( A T - A T Q ) / + Q + B T G a e T n* .
Введем новые векторные переменные q и p * так, чтобы выполнялись равенства:
d(BTGa£Tn) = BG^rf ,
p* = AT/ - BTGa£Tq = p - BTGa £Tq.(7)
Тогда окончательно получаем следующую систему уравнений движения СТТ со структурой дерева:
Mv - ST / = 0, - Sv + Aq = - vr,™
1 AT / = p * + BTGa£Tp, sGTv = 0,
p* =( AT - ATQ) / + Q,(9)
где переменные г/ связаны с множителями Лагранжа П соотношениями (6).
Особенность уравнений (8), (9) состоит в следующем.
Во-первых, уравнения (9) разрешены относительно производных обобщенных импульсов p* и не содержат замкнутых контуров.
Во-вторых, дополнительные связи (3), накладываемые на механическую систему замыканием кинематических цепей вторичного графа, учитываются в уравнениях движения на уровне кинематических соотношений (8).
Приведенный ниже пример показывает, что в этом случае численное решение оказывается более устойчивым к ошибкам вычислений, чем решения, основанные на классических методах учета дополнительных связей на уровне ускорений.
3. Методы разрешения уравнений (8) относительно обобщенных скоростей
При численном моделировании СТТ с использованием уравнений (8), (9) необходимо уравнения (8) на каждом шаге интегрирования разрешать относительно обобщенных скоростей q . Для этого из системы в первую очередь необходимо исключить дополнительные множители Лагранжа г/ .
Заметим, что, если известен вектор п , при котором удовлетворяются уравнения связей (3), то система (8) является линейной системой уравнений с симметричной, блочной квазитрехдиагональной разреженной матрицей коэффициентов относительно скоростей v , q и переменных / .
При численном моделировании ее можно легко привести к двухдиагональному виду, используя методы "прогонки", изложенные в работе [2], основанные на несимметричном (метод Верещагина) или симметричном (метод Холецкого) Гауссовом исключении.
Для примера приведем алгоритм соответствующего преобразования уравнений (8) с использованием несимметричного Гауссова исключения.
Алгоритм диагонализации уравнений (8) for i = N :1
Mi = Mi -1 H MC d,=( ATM* As'. Hi=E - Mi Ada
Pi= Pi + Airf ф ^iuCT[MADA+Hj(M j} end for i = 1: N
Кроме того, при построении системы уравнений (13) необходимо выполнить множество матричных операций, что приводит к значительным вычислительным затратам.
Выберем другой путь. Декартовый импульс Mv выразим из первого уравнения (12) и подставим в уравнение связи (10). В результате получим, что вектор n удовлетворяет следующей системе уравнений:
s G T ( Gas T n + ST S ) = ss T n + s G T S T S =
= 2 En + sGTSTS = 0.
Следовательно, вектор n определяется равен qi = Di Pi- AT (ф + Mi (Civk,+ vi))
ством n = -~sGTSTS. Подставим в послед vi = Civk,+ Aiqi +v
*= M * vi +Ф end
Пусть в первичном графе системы все раздваиваемые вершины различны, а масс-инерционные характеристики раздвоенных вершин равны. Тогда уравнения кинематических связей (3) можно представить в виде sGTMv = sGTM (Bq + ^) = 0, (10)
Введем новую векторную переменную
S = ^ - ТTGa £ T n
и преобразуем систему уравнений (8) к виду:
'Mv - S T S = G a S T n , - Sv + Aq = - vr , A T S = P *, s G T Mv = 0.
Выведем теперь итерационный алгоритм вычисления вектора n. Во-первых, за метим, что вектор п удовлетворяет системе линейных уравнений sGTMv =
= s G T MB ( B T MB )- 1 ( BTGa s T n + P *) = 0, (13) которая получается последовательной сверткой уравнений (12).
Система (13) в общем случае содержит избыточное число уравнений и неизвестных координат вектора n . Поэтому часть координат либо равны нулю, либо являются зависимыми. Решение системы уравнений (13) необходимо искать с помощью алгоритмов построения псевдообратной матрицы к матрице системы Ф = s G T MB ( BTMB ) 1 BT Gas T . например, методом сингулярного разложения этой матрицы [3].
нюю формулу выражение (11) множителя S через вектор множителей Лагранжа s . В ре- зультате получим следующее соотношение:
n = n - 1 s GTST S .
Последнюю формулу можно рассматривать как итерационную – вычисления "нового" уточненного значения вектора щ при известных "старых" значениях Щ-\ и S- 1:
n k = n k - 1 - 1 s GTST S - 1 , (14) где k – номер итерации.
Из системы уравнений (8) выразим вектор S-i и подставим в формулу (14). В результате после несложных преобразований получим, что вектор n вычисляется по итерационной формуле nk =( E - Ф )nk-1 -1 sGT MB (BT MB )-1 p *.
Отсюда следует, что формула (14) задает алгоритм простых итераций [3] приближенного решения системы линейных уравнений (13).
Нас не интересует вопрос сходимости итераций, определяемых формулой (14), хотя численные эксперименты показывают, что последовательность {щ } сходится к точному значению n для многих механических систем. Формулу (14) будем использовать для итерационного восстановления системы уравнений (13).
Введем обозначения:
Vf (n) = sGTMv = Фп + sGT MB ( BT MB )-1 p *.
Тогда Vf(nk)- Vf(0) = sGTM (vk - v0) = ФПк .
Пусть щ вычисляются по формуле (14), а векторы vk , ^ определяются с помощью представленного выше алгоритма диагонализации уравнений (8). Заметим, что в этом алгоритме операции формирования матриц M *, D и H , которые требуют наибольших вычислительных затрат, можно выполнить только один раз на первой итерации.
Совершим такое количество итераций, чтобы число столбцов в матрице A F = { f f ( П к ) -V f ( 0 ) } оказалось больше ранга матрицы Ф . Тогда псевдообратную матрицу Ф + системы линейных уравнений (13) можно найти по формуле
Ф + = X A F + , (15) где A F + - псевдообратная матрица к матрице A F , вычисляемая с помощью сингулярного разложения [3], X = { щ } — матрица, столбцами которой являются векторы щ .
После нахождения матрицы Ф + , вектор щ можно найти по формуле
П = - Ф + V f ( 0 ) = 1 Ф + S G T S T р, = - Ф + щ . (16)
Завершается итерационный алгоритм вычислением вектора обобщенных скоростей q с помощью еще одного цикла вычислений по формулам алгоритма диагонализации системы уравнений (8).
4. Пример моделирования СТТс замкнутой цепью
Для иллюстрации техники составления уравнений (8), (9), определения всех входящих в них параметров, выведем уравнения движения для механической системы – кривошипношатунного механизма (КШМ), состоящего из трех тел; кривошипа ( Т 1 ), поршня ( Т 2 ) и шатуна ( Т ш ). Расчетная схема представлена на рис. 3.
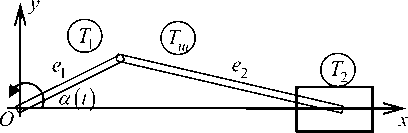
Рис. 3. Кривошипно-шатунный механизм
Система содержит одну замкнутую цепь. Размыкание проведем раздвоением шатуна Тш на два тела: Т3 и Т4. Получаемая в результате такого раздвоения механическая система со структурой дерева представлена на рис. 4. Масс-инерционные характеристики шатуна распределим пополам между телами Т3 и Т4. Структура вторичного графа КШМ задается массивом к = {0,0,2,1}. Матрица е, определяющая соответствие между образами и прообразами раздвоенных вершин, в нашем случае имеет вид е = (0 0 1 -1).
Систему координат, связанную с кривошипом, поместим в точку О , СК поршня находится в центре поршня, СК тел Т 3 и Т 4 поместим в середину стержней, моделирующих шатун.
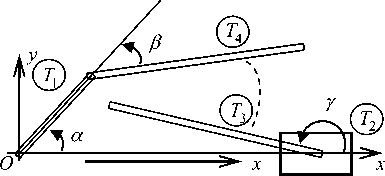
Рис. 4. Вторичный граф КШМ, к = { 0,0,2,1 } , е = ( 0 0 1 - 1 )
Пусть gj = 0.5 м - длина кривошипа, ег = 1 м - длина шатуна, тх = 1 кг , m2 = 4 кг, тш = 2 кг, m3 = m4 = 0.5тш , rc =(0.5e1,0,0)Т, J\zz = 0.25 кг • м2 , J2zz = 2 кг • м2 - массы, ненулевые координаты центров масс и моменты инерции тел системы.
Определим обобщенные координаты КШМ. Кривошип Т1 вращается вокруг точки О, угол поворота - а . Поршень Т2 совершает возвратно-поступательные движения вдоль оси Ох, соответствующую обобщенную координату обозначим через х. Положение шатуна Т3 от- носительно поршня зададим углом /, а угловые перемещения образа шатуна Т4 относительно кривошипа определим углом Д
Таким образом, система со структурой дерева имеет четыре степени свободы. Векторы обобщенных координат:
^ 1 = ( а ) , 9 2 = ( x ) , 9 э = ( г ) , q 4 = ( e ) .
Радиус-векторы р = Ok Ot зависят от обобщенных координат следующим образом:
Р 1 = ( 0,0,0 ) т , Р 2 = ( х ,0,0 ) T ,
Р з =
1 1 • oY
—e 2 cos y ,- e 2 sin / ,0 I
( 1 „1 ^T
Р 4 = I g + “ e 2 cos в , ~ e 2 sin в ,0 I
Матрицы направляющих косинусов:
|
' cos a sin а 0 |
||||
|
G 1 = |
- sin a cos a 0 |
, G 2 = E , |
||
|
{ 0 |
0 1 J |
|||
|
^ cos у |
sin у 0 |
2 cos в sin в 0Л |
||
|
G 3 = |
- sin у |
cos у 0 |
, G 4 = |
- sin в cos в 0 |
|
[ 0 |
0 1 J |
I ° 0 1 J |
||
Последними необходимо задать матрицы A , определяющие кинематику относительного движения тел системы, и их производные:
|
( 0 ^ |
( 0 ^ |
|||
|
( 0 3 ( 1 ^ 0 0 0 0 A 1 - 0 , A 2 - 0 |
, A 3 - |
1 e 22 0 |
, A 4 - |
1 e 2 2 0 |
|
0 0 1 1 J 1 0 J |
0 0 I 1 J |
0 0 I 1 J |
||
A 1 = A 2 = A 3 = A 4 = ( 0 V
Для завершения индивидуализации механической системы необходимо еще задать активные силы и моменты, действующие на тела. Система рассматривается в однородном поле силы тяжести, вектор ускорения свободного падения в абсолютной СК Оxy g = (0,-9.8м/с2,0) . Вращение кривошипа с угловой скоростью а = 1 рад / с поддержива ется вращающим моментом та - 20 (1 - а( t)) н • м.
Дальнейшие шаги по формированию матричных блоков, входящих в уравнения (8), (9) являются универсальными для любой СТТ и выполняются по рекуррентным алгоритмам, изложенным в предыдущих разделах работы.
Приведенный пример иллюстрирует тот факт, что объем информации, которую необ- ходимо подготовить для построения математической модели СТТ в форме уравнений (8), (9), минимален.
Уравнения движения КШМ интегрировались встроенной процедурой NDSolve САВ Mathematica . Результаты численного моделирования представлены на рис. 5.
График на рис. 6 показывает, что представленный алгоритм решения задачи, основанный на использовании кинематических связей (3), обеспечивает хороший уровень точности в удовлетворении дополнительных геометрических связей (4), накладываемых условиями совпадения абсолютных координат третьего и четвертого тел системы, на длительном промежутке интегрирования даже без дополнительных процедур по их стабилизации.
Для сравнения был использован классический подход к формированию уравнений движения механических систем с дополнительными связями. Уравнения динамики КШМ строились в форме уравнений Лагранжа первого рода в обобщенных координатах [4].
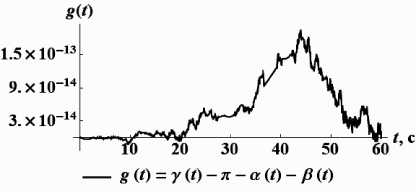
Рис. 6. Точность удовлетворения дополнительной связи
Для определения множителей Лагранжа ц* динамические уравнения замыкались один раз продифференцированными уравнениями кинематических связей (3). Получаемая в результате система дифференциально-алгебраических уравнений (ДАЕ) относительно обобщенных ускорений и множителей Лагранжа также интегрировалась процедурой NDSolve.
Как показал вычислительный эксперимент, интегрирование такой замкнутой системы уравнений движения приводит в процессе построения численного решения к значительному уходу с геометрических связей (4).
Результаты моделирования представлены на рис. 7.
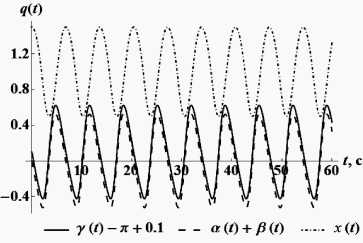
Рис. 5. Результаты моделирования
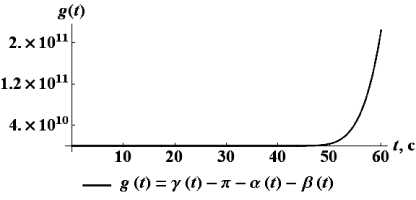
Рис. 7. Уход со связи при использовании уравнений Лагранжа первого рода
Эти результаты показывают, что при замыкании уравнений движения на уровне ускорений требуется дополнительная стабилизация связей, например методом Баумгарта [5]. При этом система ДАЕ становится более жесткой, что приводит к дроблению шага численного решения и замедлению счета. В отличие от классического подхода, интегрирование уравнений (8), (9) избавляет от указанных проблем.
Заключение
В работе получена новая матричная форма уравнений движения систем связанных твердых тел с замкнутыми кинематическими цепями. Уравнения содержат импульсы Пуассона, обобщенные координаты, квазискорости и множители Лагранжа. Выписаны рекуррентные формулы, предназначенные для компьютерного формирования уравнений из простейших основных блоков, описывающих структуру, масс-инерционные, геометрические и кинематические характеристики отдельных звеньев механической системы.
Группа кинематических уравнений, входящих в расширенную систему уравнений (8), (9), имеет квазитрехдиагональную блочную структуру относительно переменных { q , v , ^ } , что позволяет для их разрешения относительно обобщенных скоростей использовать методы "прогонки", а для определения множителей Лагранжа п , появляющихся в уравнениях в результате учета дополнительных связей (3), – итерационные методы.
Эти алгоритмы являются более быстрым для механических систем, содержащих длинные кинематические цепи, в отличие от алгоритмов моделирования СТТ, основанных на использовании уравнений в форме Лагранжа второго или первого рода.
Приведены все этапы формирования исходной информации и результаты компьютерного моделирования одной демонстрационной механической системы описанным в работе методом. Результаты показывают, что предлагаемый метод позволяет получать удовлетворительные результаты численных расчетов стандартными методами интегрирования дифференциальных уравнений, встроенными в существующие пакеты прикладных программ, без дополнительной стабилизации уравнений связей.
Список литературы Матричные уравнения движения систем твердых тел в гамильтоновых переменных. Системы c замкнутыми цепями
- Иванов В.Н. Матричные уравнения движения систем твердых тел в гамильтоновых переменных. Системы со структурой дерева // Вестник Пермского университета. Математика. Механика. Информатика. 2019. Вып. 3(46). С. 38-46.
- Иванов В.Н. Алгоритмы решения уравнений движения в импульсах Пуассона систем твердых тел со структурой дерева // Вестник Пермского университета. Математика. Механика. Информатика. 2017. Вып. 4 (39). С. 25-31.
- Голуб Дж., Ван Лоун Ч. Матричные вычисления. М.: Мир, 1999. 548 c.
- Суслов Г.К. Теоретическая механика. М.: Гостехиздат, 1946. 656 с.
- Wittenburg J. Dynamics of multibody systems. Berlin: Springer-Verlag, 2008. 223 p.


