Механизмы передачи теплоты в градирнях (теория и методы расчёта)

Градирни – смесительные теплообменники – являются высокоинтенсивными аппаратами, так как в них теплообмен происходит при непосредственном контакте (соприкосновении) теплоносителей, то есть в смесительных теплообменниках отсутствует термическое сопротивление стенки.

При охлаждении оборотной воды воздухом часть теплоты передается за счет поверхностного испарения воды – превращения воды в пар с последующим переносом пара путем диффузии в поток воздуха. Другая часть – за счет разницы в температурах между водой и воздухом, то есть теплопередачей соприкосновением (теплопроводность и конвекция) [1, 2].

Теплопередача при непосредственном контакте воздуха и вводы всегда сопровождается процессом переноса массы из одной фазы в другую. Это процесс сопряженного тепломас-сопереноса [5, 8, 9].

В нашем случае под испарением подразумевается процесс перехода воды из жидкого состояния в парообразное при температуре меньшей, чем температура кипения воды при заданном давлении.

В соответствии с кинетической теорией газов, механизм процесса испарения воды с поверхности соприкосновения ее с воздухом можно трактовать следующим образом [4, 11]. Молекулы воды находятся в хаотическом (вращательном, колебательном и поступательном) тепловом движении, а их скорости отклоняются в широких пределах от среднего значения. Молекулы, обладающие большой кинетической энергией, вылетают в пространство, расположенное над поверхностью воды, преодолевая силы молекулярного сцепления. Эти молекулы при столкновении с молекулами воздуха изменяют величину и направление своего движения. Часть молекул воды возвращается обратно в воду. Другая часть молекул удаляется от поверхности воды, проникает в воздух в результате диффузии и конвекции и уже безвозвратно теряется водой, образуя водяной пар в воздухе.

В непосредственной близости к поверхности воды воздушная фаза насыщена паром и при этом парциальное давление p п равно давлению насыщенного пара P п при температуре жидкости. Поскольку в рассматриваемом случае р п <  Р п , то возникает поток вещества из жидкости в воздушную фазу. Переносимая потоком энергия запишется как q п r , где r – энтальпия испарения.

Поскольку в процессе испарения вода охлаждается, то источником энергии q п r является сама вода. В нашем случае испарение происходит за счет переноса теплоты от воздуха к воде и ее охлаждения (процесс адиабатного испарения).

При адиабатном испарении вода охлаждения до температуры мокрого термометра t м.т. – наинизшей температуры воды, испаряющейся в движущуюся над ней парогазовую смесь.

Значение t м.т определяется равенством потоков теплоты, передаваемой воздухом воде за счет конвекции [α( t в – t м.т )] и переносимой из жидкой фазы в воздушную вследствие испарения ( q п r ):

α( t в – t м.т ) = q п r , (1) где t в – температура воздуха, α – коэффициент теплоотдачи.

Основываясь на кинетических закономерностях массопереноса, определяется величина q п r . Из уравнения (1) следует:

α = q п r / ( t в – t м.т ),              (2)

t м.т = t в – q п r /α

Уравнение (1) решается, следовательно, путем анализа тепломассопереноса.

Принято считать, что основное сопротив- ление процессу теплопередачи в системах газ – жидкость сосредоточено в газовой фазе. При этом для расчета кинетики процесса целесообразно воспользоваться выражением (1).

Таким образом, в градирне всегда имеет место испарение. Но поскольку испарение связано с затратой теплоты на изменение агрегатного состояния, то оно вызывает поток теплоты Q u только от воды к воздуху (отвод теплоты), то есть охлаждение воды. Поток теплоты за счёт соприкосновения Q с также направлен от воды к воздуху. Результирующее количество теплоты Q составит:

Установлено, что отвод теплоты испарением преобладает над теплоотдачей соприкосновением.

Тепловой баланс системы производственное оборудование – градирня имеет вид:

(5) где Q об – количество теплоты, выделяемое оборудованием; Q гр – количество теплоты, отводимое холодным воздухом в градирне.

На основании этого запишем уравнение теплового баланса, позволяющее определить расход воздуха G в на охлаждение воды:

G • c ( t H — откуда

t k ) = G . • С в ( 1 2 - ^

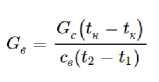
где G – расход охлаждаемой воды; с – средняя удельная теплоёмкость этой воды; с в – удельная теплоёмкость воздуха; t н , t к – начальная и конечная температура охлаждаемой воды; t 1 , t 2 – начальная и конечная температура охлаждающего воздуха.

Уравнение теплового баланса можно записать иначе:

^(т^- ~ ^(т;К; ⁼ ^К ~ ⁽'ЛК,. ~ Q” (8)

Откуда

_ \G(\-h_K)-Q„]

^л К_;-^ (9)

где G - расход охлаждаемой воды; h н и h к -начальная и конечная энтальпия охлаждаемой воды ( h = ct , где с - теплоемкость, t - температура теплоносителя); h н . в и h к.в - начальная и конечная энтальпия охлаждающего воздуха; Q п - потери теплоты в окружающую среду.

При теплотехнических расчетах задаются: средней максимальной температурой воздуха наиболее теплого месяца; средней месячной относительной влажностью воздуха в 15 ч наиболее тёплого месяца; атмосферным давлением; температурой воздуха по психрометру.

Теория мокрого термометра [10] основана на использовании процесса сопряжённого тепломассопереноса в движущейся среде в близи поверхности раздела фаз с целью расчёта стабилизированного значения температуры мокрого термометра t м.т.

В стационарном состоянии поток теплоты, направленный внутрь воды, равен изменению энтальпии на её поверхности:

1'^ -^ ^ — "'"“^'"(гт) (10) 1 — е ~ 9х / где а - коэффициент теплоотдачи, независящий от движущей силы процесса; tм.т - температура мокрого термометра; Cо - коэффицент Эккермана, зависящий от мольного потока компонентов и коэффициента теплоотдачи; r - теплота испарения на межфазной поверхности; в - коэффициент массоотдачи, не зависящий от движущей силы процесса; p - полное давление в двухфазной системе: g - мольная доля; gк - концентрация на межфазной поверхности.

Используя аналогию между коэффициентами теплопередачи и массопередачи, получим уравнение:

^-^'т^^^-¹¹ Н,—) (11)

где в - поправочный коэффициент (обычно принимается в = 1); С р - мольная теплоёмкость компонента; Le = Pr / Sc - число Льюиса для жидкости; Pr , Sc - числа Прандтля и Шмидта для жидкости или DC р р / Л , где D - коэффициент диффузии в жидкости; р , Л - соответственно плотность и коэффициент теплопроводности жидкой фазы.

Уравнение (11) позволяет найти t _м .т для фиксированных значений g и t . После введения ряда приближений для фактора Эккермана и с учётом незначительной разности температур и парциальных давлений при использовании показаний t м.т , уравнение (11) принимает вид:

" - '    = —■ ■  (^ - !l)     (12)

При измерении влажности для системы воздух-вода погрешность в результате допущенных приближений не превышает 2-3%. Если использовать значения влажности воздуха W = Мад/Мв(1 - g) и массовой теплоёмкости паровоздушной смеси Cs = св+ Wcа то уравнение (12) можно записать в виде:

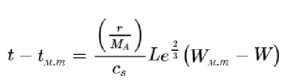
где M i , M в - молекулярные массы жидкой фазы и воздуха; с в - теплоёмкость паровоздушной смеси.

При практическом применении уравнения (12) в случае системы вода-воздух, для которой Le²³ = 1, число Льюиса в уравнении опускают, тогда уравнение (13) приобретает вид:

^-{тп)^ = f''■ :--(ж )и ■■ ■(14)

Вследствие небольших изменений тепло- емкости с изменением температуры, этими изменениями пренебрегают. Тогда на поверхности шарика мокрого термометра энтальпия насыщенного воздуха на единицу массы будет равна энтальпии смеси воздух-вода в объёме.

Иными словами разность между температурой сухого термометра t с и температурой мокрого термометра t м.т. пропорциональна влажности воздуха: чем суше воздух, тем больше разность t с - 1 м.т. ; если же воздух насыщен паром, то t с = t м.т ., так как парциальное давления водяного пара в воздухе равно давлению насыщения водяного пара при той же температуре t с . Поскольку психометрическое отношение приблизительно равно единице, то температура мокрого термометра практически та же, что и температура адиабатического насыщения в системе воздух-вода. На практике значение t м.т -■ const , однако значения t и W изменяются.

Зачастую возникает задача определения средней разности энтальпии воздуха в градирне, локальные значения которой могут существенно изменятся [3]. Обычно для расчета используется уравнение Меркеля, выражающее общее количество теплоты передаваемое в результате совокупности конвективного теплообмена и изменения агрегатного состояния вещества- испарения воды. Движущей силой является разность энтальпий (теплосодержаний) влажного воздуха.

Уравнение Меркеля имеет вид:

dQ = в х ( h ''- h ) dF          (15)

где Q - количество передаваемой теплоты; в х -коэффициент массоотдачи, отнесенный к разности влагосодержаний воздуха; h" - энтальпия насыщенного влажного воздуха при температуре поверхности воды; h - энтальпия влажного воздуха в основном потоке; F - поверхность.

Поскольку уравнение (15) относится к элементам поверхности контакта воды и влажного воздуха, возникают трудности при правильном осреднении разности энтальпий воздуха.

Количество передаваемой теплоты находим из уравнения:

^Q = вЛ, = -G^F (16) к где Gв и Gж - расходы воздуха и воды; k - поправочный множитель; сж - теплоёмкость воды; t - температура воды.

Из (15) и (16) запишем:

Gplh = -G^Gt = -ipG' -h^SF (17)

Уравнение (16) в интегральной форме:

Q = G_;G: -bp=iG_:p^^ Г AF^F ⁽¹⁸⁾

где индексы 1 и 2 обозначают начальные и конечные значения параметров. Величина A h ср -средняя по поверхности разность энтальпий воздуха h "- h , дельта h ср = h" - h .

Используя объёмный коэффициент массоот-дачи ev = в х F/ V , отнесенный к единице активного объёма аппарата V = H F а (где Н - его высота, а F а - площадь сечения активного объёма), из уравнений (17) и (18) находим формулы для расчёта поверхности F , активного объёма V а и высоты Н а на градирни, тогда имеем:

л, h^ - hi ^—нГ

h - Ъ Н₂

Л.Д. Берманом получена другая формула для средней логарифмической разности энтальпий:

h2 - hi Ahi - Ahi

Л ~        ~               (20)

^Ш ДЬ, Sh"

Формула (20) обеспечивает большую для практических расчётов точность получаемых результатов по сравнению с (19).

Аэродинамический расчёт вентиляторных градирен заключается в установлении соответствия полного аэродинамического сопротивления градирни напору, развиваемому вентилятором [4, 6].

Полное аэродинамическое сопротивление P представляет собой сумму сопротивлений её элементов: входа воздуха в градирню P 1 ; воздухораспределителя P 2 ; поворота потока воздуха в ороситель P 3 ; внезапного сужения при входе воздуха в ороситель P 4 ; оросителя P 5 ; внезапного расширения при выходе воздуха из оросителя P 6 ; водоуловителя P 7 ; водораспределителя P 8 ; входа воздуха в вентилятор P 9 и выходного патрубка из вентилятора P 10 :

р ₌ р₁_р_:_р._р₁_р._р.__р._р_:._р.₁_ р^ (21)

Величины сопротивлений входящую в правую часть выражения (21), рассчитываются по формуле:

. ..К = Sl.2 .JU Д ( )

где: £ i,2.,io - коэффициент сопротивления элементов градирни; ю 1,2...,10 - скорость движения воздуха в элементах градирни; р - плотность воздуха.

Коэффициент £ 1 для определения сопротивления Р 1 , отнесённый к скорости воздуха во входных окнах градирни, рекомендуется принимать:

£ 1 = 0,55                (23)

Коэффициент сопротивления воздухораспределителя ^ 2 рассчитывается по формуле:

Л=(о.1-и.1йЧ;)<.        (24)

где q ж - плотность орошения градирни; d э - эквивалентный диаметр воздухораспределителя.

Коэффициент сопротивления поворота потока в ороситель, отнесенный к скорости воздуха в оросителя, рекомендуется принимать равным:

£3 = 0,5(25)

Величина коэффициента сопротивления ^ 4 определяется по формуле

S. = 0,511 -f | где fj - площадь живого сечения оросителя; f - площадь всего сечения оросителя.

Коэффициент сопротивления всего оросителя:

£ 5 = £ 5 h               (27)

где h - высота оросителя, c - коэффициент сопротивления сухого и мокрого оросителя [2]. Коэффициент сопротивления выхода потока из оросителя:

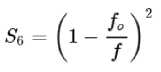
Здесь величина коэффициента отнесена к скорости в живом сечении оросителя.

По Идельчику [6] величина коэффициента сопротивления водоуловителя ξ 7 определяется по формуле:

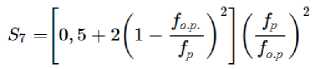
где f о.р . и f р – соответственно площади живого сечения и общая водоуловителя.

Коэффициент сопротивления водораспределителя можно рассчитать по формуле [6]:

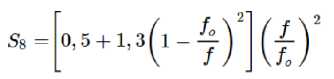
где f о – площадь живого сечения водораспределителя; f – общая площадь устройства.

Предложена зависимость для определения коэффициента сопротивления входа воздуха через конфузор в вентилятор [4]:

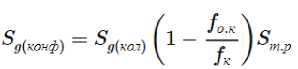
Здесь f k и f о.k. – площадь сечения до и после сужения; Sg(кол) – коэффициент сопротивления конического коллектор; ξ g(кол) – коэффициент сопротивления трения.

Если выходной патрубок имеет форму диффузора, то его коэффициент сопротивления

510 =(1 + ^S^        (32)

где σ – поправочный коэффициент; ξ – коэффициент сопротивления расчётный.

Значения обоих коэффициентов приведены в специальной литературе.

Потери воды при работе градирен неизвестны.

Допуская, что вся теплота передаётся от воды только за счёт испарения, запишем:

C„r яй G_x Д tc^           (33)

где Gu – количество испарившейся воды; r – теплота парообразования; G ж – гидравлическая нагрузка градирни; ∆ t – перепад температур воды; с ж – удельная теплоёмкость воды.

Из (23) получаем выражение для определения количества испарившейся воды в процентах от общего расхода циркуляционной воды:

G Ate n= ^-100 =---100 = aAt (34)

где a – поверхность охлаждения, a = —100          (35)

Потери воды в виде капель из-за уноса существенно зависят от конструкций водораспределителя и каплеуловителя градирни, а также от их исправности. Принимаются потери за счёт уноса 0,3–0,5% от циркуляционного расхода воды [11].

Потери воды на фильтрацию малы и их при расчёте не учитывают.

Величина потери на продувку (сброса части воды из циркуляционной системы с целью ограничения солесодержания воды) определяется в зависимости от качества добавочной (свежей) воды. Потери могут составлять 0,5–5%

Изложенные в работе теоретические и практические материалы послужат полезной информацией для совершенствования действующих и разработки новых конструкций градирен.