Механизмы управления маневрированием шагающей машины с ортогональными движителями

В работе рассматриваются шагающие машины с ортогональными движителями, у которых движения продольного перемещения корпуса относительно опертых ног, находящихся в рабочей фазе шага, а также переноса ног вдоль корпуса в фазе переноса и движения подъема–опускания ног кинематически разделены. Продольное перемещение корпуса относительно опорной поверхности обеспечивается плоскими механизмами горизонтального перемещения (МГП) движителей, все звенья которых движутся в плоскостях, параллельных горизонтальной плоскости корпуса. Поэтому как прямолинейное перемещение, так и поворот таких шагающих машин могут рассматриваться как задачи плоскопараллельного движения [1].

Если принять за опорную точку ноги центр ее стопы, то в плоскопараллельном движении траектории и вектора скоростей опорных точек каждой из ног относительно корпуса будут представлены их проекциями на его горизонтальную плоскость. При повороте векторы проекций скоростей опорных точек ног в рабочей фазе должны отклоняться от продольной оси машины и быть ориентированы относительно центра поворота аналогично тому, как плоскости вращения управляемых колес автомобиля. Кроме того, значения горизонтальных составляющих скоростей должны иметь значения, пропорциональные расстоянию каждой опорной точки от центра поворота [2].

Постановка задачи

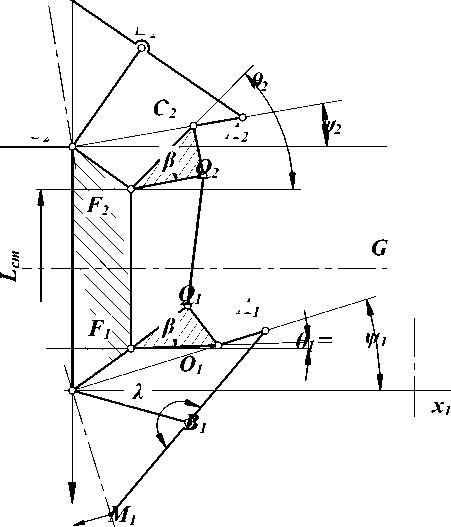
У ортогональных движителей, МГП которых построены на основе лямбдообразных механизмов Чебышева (ЛМЧ) с углом излома шатуна X = 180 ° , отклонение вектора скорости от продольной оси корпуса определяется углом у наклона основания ОС механизма, а величина скорости V_М регулируемым параметром d – длиной основания ОС (рис. 1) [3]. Точку С , совпадающую с осью вращательной пары С, которой МГП присоединено к корпусу и координатами которой определяется положение МГП относительно корпуса, назовем расчетной точкой МГП. Синхронное изменение величин у и d относительно расчетной точки производится поворотом управляющего звена FO , размеры которого и положение оси вращения определяются при проектировании МГП. При этом параметр d и угол у отклонения основания МГП в зависимости от угла поворота 9 этого звена как параметра будут иметь значения (см. рис. 1):

d = X Fp + y p + l y + 2 • l y • (x p • cos 9 + y p • sin 9 ),

Л, • sin 6 + yF

V = arctg; ----——,                         (1)

l у • cos6 + xp где ly – длина управляющего звена;

x F , y F – координаты оси вращения управляющего звена в системе кооpдинат, связанной с расчетной точкой С МГП;

• 6 - угол поворота управляющего звена.

При объединении всех МГП машины в кинематическую систему горизонтального перемещения для движения машины с заданной кривизной поворота каждая из опорных точек перемещается со скоростью, имеющей строго определенное значение, которое должно быть согласовано со значениями скоростей остальных опорных точек. Поэтому управляющие звенья МГП должны соответственно занимать определенные, согласующиеся между собой положения. Эти положения можно задавать каждому из управляющих звеньев отдельно при помощи специального привода. Кроме того, положения управляющих звеньев можно согласовать, связав кинематически их перемещения между собой при помощи, например, передаточных механизмов. Тогда перемещение одного из управляющих звеньев приведет к согласованному изменению положений остальных звеньев.

Рулевые механизмы пояса

Для унификации движителей все МГП (их расчетные точки) размещаются симметрично относительно продольной и поперечной осей корпуса, а расчетный центр поворота размещается на поперечной оси с радиусом поворота центра корпуса R (или кривизной K = 1/ R ). Линию С 1 С 2 размещения расчетных точек (см. рис.1), параллельную поперечной оси корпуса, назовем поясом. Положение пояса относительно центра корпуса G определяется расстоянием D . Расстояние от расчетных точек вдоль пояса от продольной оси корпуса равно В – половине ширины корпуса.

У соседних МГП с различными значениями координат расчетных точек углы поворота, определяющие положения их управляющих звеньев, связаны между собой нелинейными зависимостями. Углы поворота 6 1 и 6 2 управляющих звеньев МГП, расположенных на одном поясе и определяемые зависимостями вида (1), будут связаны значением радиуса поворота R через углы ^ 1 и ^ 2 (см. рис. 1):

, Г D ) ^ 1 = ^arctg ПГ“^1 , V R — в )

. Г D ) ^v 2 = ^arctg V в )

Приравняв соответствующие выражения (1) и (2), исключив R , получим

где

2 • B cos61 • ly + xF Ц =+--,

D   sin 6 1 • l y + y p

l y = F 1 O 1 = F 2 O 2 .

Зависимость (3) можно воспроизвести при помощи двухкоромыслового шарнирного передаточного механизма, у которого коромысла жестко соединены с управляющими звеньями. Для МГП одного пояса, которые одинаковы, это будет симметричный механизм, аналогичный рулевой трапеции автомобиля, и который назовем рулевым механизмом пояса (см. рис. 1). Исходными данными для синтеза рулевого механизма пояса будут длина стойки:

L cm = 2 • ( B + y p )

и функция (3), которую механизм должен воспроизводить на участке между предельными углами поворота 6н и 6в коромысел FiOi и F2O2 :

6Н в н,в

a • b + D • K_max •-./ c • 1 2 — b ² max        y

= arcsin-----------------y----------- сly

Для определения О н подставляется j= +1, 0 в - j= -1. Синтез механизма может быть выполнен любым из методов синтеза передаточных механизмов [4]. В результате синтеза определяются длина рулевого рычага Z FQ = Z fq^ , длина шатуна Z qq и угол развала в между управляющим звеном и коромыслом - рулевым рычагом механизма. Для возможности выбора варианта параметров механизма, оптимального с конструктивной точки зрения, необходимо использование вычислительной техники.

V M2 М²

D

B 2

= θH x2

C 2

y 2

»9

»9

A 1

O 2

A 2

y 1

V M1

C 1

Рис. 1. Механизмы горизонтального перемещения и рулевой механизм пояса

V G

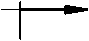
У шагающей машины с N МГП ( N - четное число при принятом симметричном расположении МГП), число поясов равно N /2. Рулевые механизмы пояса проектируются для тех поясов машины, у которых различные значения параметра D . У поясов с равными значениями D рулевые механизмы будут одинаковы.

Продольные рулевые механизмы

После того как положения управляющих звеньев МГП каждого из поясов машины увязаны между собой при помощи рулевых механизмов, возникает задача согласования положений управляющих звеньев (коромысел рулевых механизмов) МГП различных поясов машины. Выясним, какие положения относительно друг друга должны занимать управляющие звенья МГП, которые расположены на одном борту.

У поясов с одинаковыми значениями D управляющие звенья МГП должны перемещаться синхронно, на одну и ту же величину.

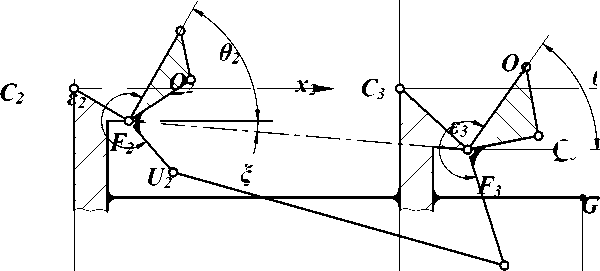
У поясов с различными значениями D углы поворота управляющих звеньев 0 ₂ и 0 ₃ связаны зависимостью (рис. 2):

x F ₂ ^- y F ₂ ^{+ c} 'д ¹ 2 ' ( ^{1 + c 2} ) ^- (c ' ^x F ₂ ^{- y} F ₂ ) ²

02 = arcsin-----------------------------х--------------------,                   (4)

Z y ₂ ' ( 1 + c ² )

где

= D ₂ l y ₃ ' ^{sin 0} 3 ⁺ y F ₃

.

D₃ Z y 3 • cos 0 ₃ + x_F 3

Воспроизведение этой зависимости производится продольным четырехзвенным передаточным рулевым механизмом. Исходными данными для проектирования механизма являются длина стойки:

LF2 F3 = V t 2 + 5 2, где t = D2 - Dз - xF2 + xF3 ,     S = yF2 - ур3 , y3

y 2

O 2

Q 3

θ 3

B

U 3

D 3

x 3

D 2

Рис. 2. Продольный рулевой механизм для МГП поясов с различными значениями D

Функция перемещения (4) и предельные углы поворота управляющих звеньев, которые определяются в процессе синтеза рулевых механизмов соответствующих поясов. Угол наклона ^ стойки продольного рулевого механизма к продольной оси корпуса найдем по формуле:

^ = arctg

s t

Для синтеза механизма используются известные методы синтеза передаточных механизмов

• [4] . В результате синтеза определяются длины коромысел I f^ и I fu , длина шатуна l uu и

• углы £2 и £3 между управляющими звеньями и коромыслами механизма.

Y 3

U 2

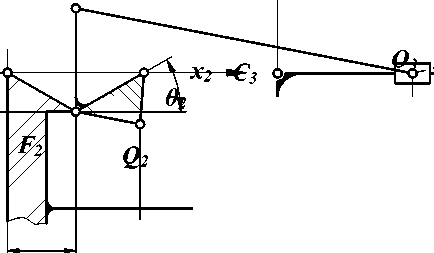
dnH xF

D H

D H

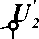
x F

Рис. 3. Продольный рулевой механизм шестиногой шагающей машины

При симметричном расположении поясов у шестиногой шагающей машины появляется особенность, связанная с тем, что для рулевого механизма центрального пояса D = 0 и угол наклона основания МГП равен нулю. В этом случае управляющее звено представляет собой ползун (рис. 3). Перемещение ползуна удобнее согласовать с поворотом управляющего звена соседнего пояса при помощи продольного рулевого механизма в виде кривошипно-ползунного механизма. Перемещения ползуна по функции вида d = f (r, X, B, D, R) [3] должны согласовываться с углами поворота кривошипа 9 по (1) и (2) при принятом в качестве параметра радиусе поворота центра корпуса R. Эксцентриситет кривошипно-ползунного механизма е равен e = |yF |, а расстояние от оси вращения кривошипа до начального положения ползуна (которое соответствует случаю движения машины по прямой) в зависимости от положения механизмов соседнего пояса (см. рис. 3):

X F 2 O ₃ = ^Dh ± ⁽ x F ^- d пн )

Знак плюс - для кривошипно-ползунного механизма F₂U₂O₃ и знак минус - для механизма F'₂U'₂O₃. Величина d_пн определяется по известной формуле [3]:

d пн = (r + 2)/3, где r - длина кривошипа ОА ЛМЧ (см. рис. 1).

При необходимости величины е и lp о могут быть изменены, однако при этом усложня ется конструкция машины.

Структурная схема механической системы управления маневрированием

Полная структурная схема рулевого управления восьминогой шагающей машины показана на рисунке 4. Точками С обозначены расчетные точки МГП, а точки О совпадают с осями вращения кривошипов МГП, которые на рисунке не показаны. Эта схема состоит из двух одинаковых частей-модулей, расположенных по обе стороны центра корпуса G и соединенных антипараллело-граммным механизмом F₇U'₇U'₆F₆. Схема каждого из модулей включает в себя два попарно одинаковых рулевых механизма пояса F i Q i Q₈F₈, F₄Q₄Q₅F₅ и F₂Q₂Q₇F₇, F₃Q₃Q₆F₆, одинаковые продольные рулевые механизмы F₈U₈U₇F₇ и F₅U₅U₆F₆. Поворот одного из коромысел F₆U₆ или F₇U₇ приводит к согласованному перемещению всех управляющих звеньев МГП машины.

Из рисунках 3, 4 видно, что такое управление может быть достигнуто применением четырех -звенных передаточных механизмов только при цельном, жестком корпусе. В то же время корпус должен иметь переменную структуру и число подвижностей, равное числу опертых ног [1,3]. Цельным или однозвенным корпус будет только при числе опертых ног, равном трем. Когда на опорную поверхность опустится четвертая нога, число подвижностей корпуса должно стать рав -ным четырем, что достигается при корпусе, состоящем из двух звеньев-модулей, соединенных, например, вращательной парой. При большем числе опертых ног число сочленений и модулей корпуса увеличивается. Наличие же сочленений, например между соседними поясами, делает необходимым применение для согласования положений управляющих звеньев МГП не четырехзвенный передаточный механизм, а устройство значительно большей сложности.

C 8

C 5

'

O 5

O 7

O 6

O 8

C 7

Q 5

C 1

F 5

U 5

Q 3

Q 4

O 1

O 4

O 3

C 4

O 2

Рис. 4. Полная структурная схема рулевого управления восьминогой шагающей машины

Q 6

F 6

U 6

Одним из путей сохранения преимуществ рассмотренного выше рулевого управления шагающей машиной с одновременным удовлетворением требованию необходимой структуры корпуса является ограничение выбора походок таким образом, чтобы число составных модулей корпуса было не более двух. Перемещения звеньев рулевых механизмов сочлененных модулей-полукорпусов могут быть согласованы между собой посредством специальной трансмиссии с постоянным передаточным числом, связывающей перемещения управляющих звеньев МГП, которые расположены на поясах с одинаковыми значениями параметра D .

Заключение

Введение рулевых механизмов позволяет управлять маневрированием шагающей машины от одного привода, аналогично тому, как это производится у автомобиля. По изложенной методике написана программа «Руль», которая позволяет производить проектирование в диалоговом режиме с возможностью корректировки как получаемых, так и исходных параметров. Исходными данными служат параметры пояса D и В , ширина следовой дорожки А , минимальный радиус поворота R min и радиус кривошипа r . В результате проектирования получаем длину l y и координаты x F , y F оси вращения управляющих звеньев, длины звеньев рулевого механизма пояса и угол развала β между управляющим звеном и рулевым рычагом.

Методика проектирования и программа «Руль» апробированы при расчете рулевых механизмов экспериментальных макетов шестиногой и восьминогой шагающих машин.