Механизмы в структуре виброзащитных систем: математические модели, оценка динамических свойств (часть II)

В первой части статьи (Вестник ВСГУТУ. ‒2014. ‒ № 6 (51). ‒ С. 37‒44) рассматривались вопросы, связанные с обобщением постановки задач вибрационной защиты, что нашло отражение в представлениях о возможностях расширения состава типовых элементарных звеньев механических колебательных систем. Последнее достигается расширением понятия о вибро-защитном устройстве (ВЗУ), которое может включать в свой состав различные механизмы. В структуре виброзащитной системы такие механизмы не изменяют числа степеней свободы системы в целом, а параметры вводимых дополнительных связей используются для настройки ВЗУ [1 ÷ 3]. Введение в структуру виброзащитной системы механических цепей и механизмов рассматривается как введение дополнительных связей, имеющих природу обобщенных пружин, характеризующихся приведенной жесткостью, зависящей, в общем случае, от частоты внешнего воздействия, т.е. обладающих динамической жесткостью.

Построение математических моделей механических колебательных систем с дополнительными связями, в частности, виброзащитных систем, целесообразно проводить с использованием структурных методов. В рамках таких подходов на основе преобразований Лапласа исходных математических моделей в виде дифференциальных уравнений могут быть введены в рассмотрение структурные модели-аналоги в виде структурных схем эквивалентных в динамическом отношении систем автоматического управления. В этом отношении интерес представляют передаточные функции систем и соответствующие методы динамического синтеза [4, 7 ÷ 9].

Учет особенностей механизма в структуре механической колебательной системы

Рассматриваются вопросы построения математических моделей механических колебательных систем, в том числе, виброзащитных систем, в составе которых используются различные механизмы, взаимодействующие с типовыми элементами. В качестве примера на рисунке 1 приведена расчетная схема виброзащитной системы поступательного типа с рычажным механизмом второго рода [1].

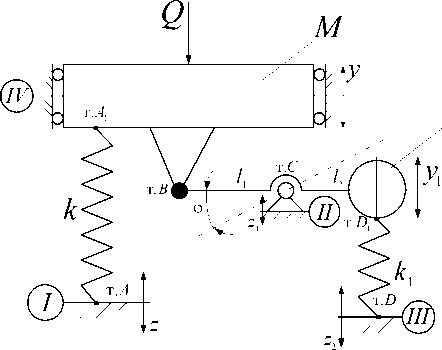
Рис. 1. Расчетная схема виброзащитной системы с рычажным механизмом второго рода

m

Для движения по координате у уравнение движения принимает вид:

у • ( м + mi ² ) p ² + у • ( k + k_xi ² ) = z 1 • ( mip ² + k_xi ) + z • ( mp ² i ² + k + k_xi ² ) — k_xi • z 2 ,        (1)

где i = l 2 / l 1 – передаточное отношение рычага второго рода.

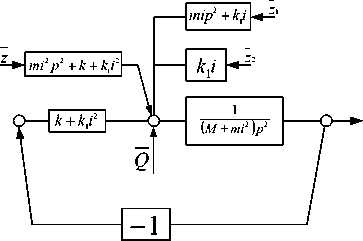
Структурная схема системы в соответствии с (1) имеет вид, как показано на рисунке 2.

y

Рис. 2. Структурная схема виброзащитной системы с рычажным механизмом второго рода

При введении рычажного механизма и учете возможных внешних возмущений в предположении, что действует только кинематическое возмущение, получим передаточную функ- цию в виде:

mi ² p ² + k + k, i ²

( M + mi ² ) p ² + k + k_vi ²

W 2 ( p ) = y

Q=0     Z z1 =0

Z 2 = 0

Структурная схема, приведенная на рисунке 2, может быть преобразована к виду, как показано на рисунке 3 а, б, что необходимо для определения динамических реакций, которые определяются параметрами обратной связи относительно объекта защиты

( 1 A I Mp-

(на ри-

сунке 3 принято, что z = z 1 ; z 2 = 0).

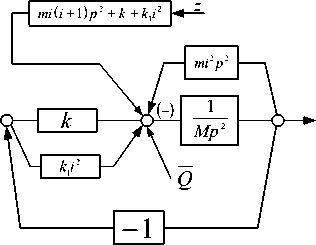
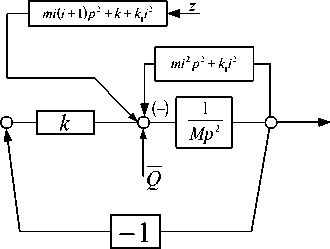
Рис. 3. Структурная схема виброзащитной системы: а ‒ с рычагом второго рода при введении дополнительной отрицательной обратной связи на основе элемента mi²p² ; б ‒ введение дополнительной обратной связи на основе упругого элемента k 1

Использование рычага первого рода обеспечивает формирование другой системы динамических взаимодействий, что находит отражение в структуре выражений для передаточных функций [10, 11]. Особенности устройств для преобразования движения, т.е. механизмов, заключаются в том, что они дополнительно формируют силу, зависящую от относительного ускорения, что качественно изменяет свойства системы. В этом плане для приложений представляет интерес расчетная схема виброзащитной системы на рисунке 4.

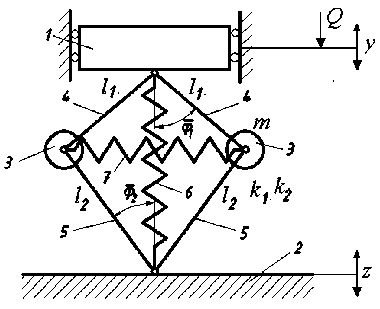
Рис. 4. Принципиальная схема дополнительной связи: 1 – объект массой m; 2 – основание; 3 – сосредоточенные массы m 1 ; 4 – тяги длиной L 1 ; 5 – тяги длиной l 2 ; 6 – упругий элемент жесткостью k 1 , 7 – упругий элемент жесткостью k 2

Если пренебречь влиянием члена уравнения, содержащего ф ² , а также допустить, что величины Ф ² , <3 , <4 являются малыми, то математическая модель рассматриваемой системы приобретает упрощенный вид линейного уравнения:

a ii У + k ii У = « 12 z + k ii ^z ,              (³)

где

„ -м + ч™    cos ^ )    , _n       cos ⁽^ i ) cos ^ 2 ) cos ⁽^ i + ^ ) .

a 11 M + ² m   2/           a 12 = ² m

Sin ( ^ + < ^₂ )                      sin ( ^ + 9₂ )

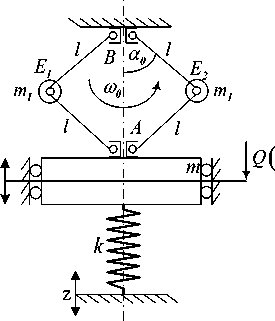
Исследованы зависимости приведенных масс и жесткостей системы от геометрических параметров механизма. Аналогичным образом могут быть получены математические модели системы при учете вращения двухзвенников вокруг вертикальной оси (рис. 5). Вращение с угловой скоростью шо придает системе ряд особых динамических свойств, формируемых действием центробежных сил инерции, создающих эффект действия пружины с отрицательной жесткостью [4].

y

t )

а

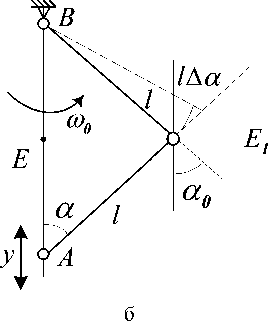
Рис. 5. Расчетные схемы: а ‒ системы со связью по абсолютному отклонению; б ‒ схема для определения параметров движения

При силовом возмущении Q ( t ) (при z = 0) передаточная функция имеет вид:

W (p )=y =

m +

m ₁

2 sin ² a

I p ² + k

—

m_x • ш₀ cos a₀

2 sin ² a

откуда следует, что при определенных условиях становится возможной практическая реализация упругих элементов с отрицательной жесткостью. Более сложные формы механических систем предполагают учет возможностей упругих взаимодействий между звеньями рычажных механизмов, что позволяет формировать в виброзащитных системах дополнительные динамические режимы, в том числе с возможностями проявлений гашения колебаний и др.

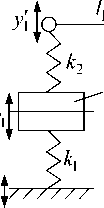
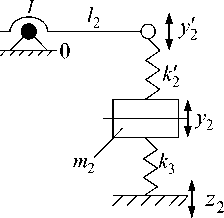
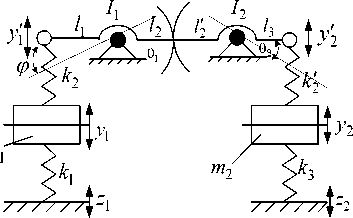
Методика построения математических моделей может быть изложена на примерах механических систем, приведенных на рисунке 6.

m ₁

ϕ

б

Рис. 6. Расчетные схемы механических колебательных систем с рычажными связями: а – рычаг 1-го рода; б – рычажная связь с зубчатым зацеплением

В предлагаемой методике могут учитываться инерционные свойства рычажных механизмов. Показано, что механические системы, имеющие звенья вращательного типа, могут приводиться к эквивалентным в динамическом отношении системам поступательного движе- ния с соответствующими приведенными характеристиками, в частности, упругими, что пока- зано на рисунке 7.

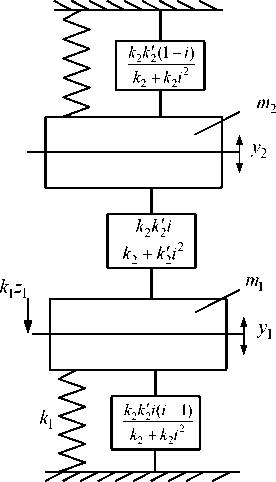
Рис. 7. Расчетная схема системы, приведенной к цепному виду и содержащей рычажные связи

Особенностью системы на (рис. 7) является то, что рычажные связи вводятся в структуру компакта упругих элементов (или квазипружины), что ранее в научной литературе в таком представлении не рассматривалось. В теории цепей для учета рычажных связей применяются специальные приемы, которые не в полной мере отражают особенности динамических связей. В механических системах связь между парциальными системами, в физическом смысле, реализуется через рычажный механизм, который вращательное усилие превращает в силовые факторы взаимодействия между массами m и m в соответствии с теоретическими положениями механики. Таким образом, система с рычажными связями может быть представлена цепной системой с упругими элементами, образующими некоторые компакты (квазипружины); связи между парциальными системами имеют упругий характер; при этом массоинерционные свойства рычага для статических расчетов полагаются малыми. Тип рычажного устройства имеет значение для построения передаточных функций системы.

Некоторые приложения метода структурных преобразований

Рассматриваются особенности формирования динамических связей в системах с объек-

том защиты в виде твердого тела в плоском движении, что характерно для задач динамики транспортных машин. Для таких систем характерны инерционные связи между парциальными системами. Возможности изменения динамических свойств системы в целом при введении дополнительных связей, реализуемых рычажными механизмами, показаны на рисунке 8.

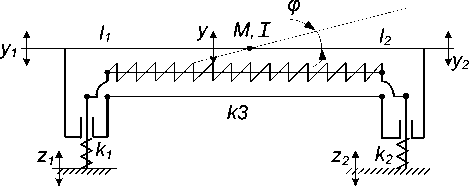
Рис. 8. Расчетная схема ВЗС с дополнительной межкоординатной связью k 3

Структурная схема системы на рисунке 9 дает представление о математической модели системы.

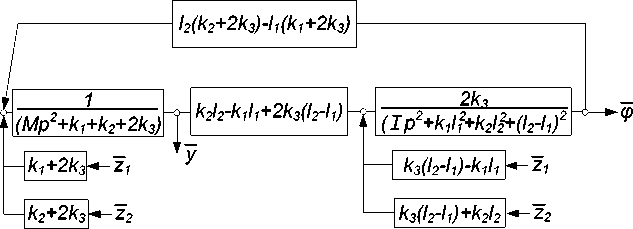
Рис. 9. Структурная схема ВЗС в системе координат y и φ

Новые связи могут изменять частоты собственных колебаний, а также частотные характеристики с формированием дополнительных динамических режимов.

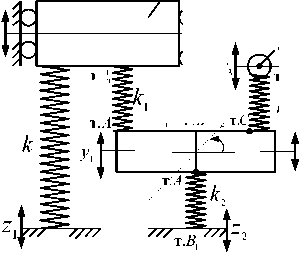
На рисунке 10 приведены исходные расчетные схемы виброзащитной системы, в которой может быть выделен динамический гаситель рычажного типа.

k

M

z

т . A 1    k

y1 т.A   k y2

т . C 1

k ₄ т . B

y ₄

y ₃

т. А k3

т . B      z ²

т . C

M y3

m ₁ т . C 1 k ₃

y

т.A y2

б

т . A

l 1    т . B l 2

а

Рис. 10. Расчетные схемы рычажного гасителя с учетом упругих свойств сочленений и рычага: а ‒ учитываются упругости во всех шарнирах и упругость рычага;

б - учитываются упругости шарниров, рычаг имеет упругость k , k₃

Упрощенная принципиальная схема рычажного динамического гасителя приведена на рисунке 11. Разработана методика расчета основных параметров рычажного динамического гасителя колебаний, исследованы динамические свойства системы при различных внешних воздействиях. Экспериментально изучались свойства гасителя на основе его лабораторного макета. На рисунке 11 показана принципиальная схема установки [12, 13].

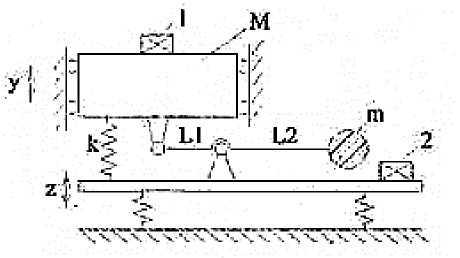
Рис. 11. Принципиальная схема установки:

1 – датчик выхода; 2 – датчик входа; y – выход; z – вход; k – коэффициент упругости пружины; M – защищаемый объект; m ‒ пригруз

Заключение

На основе изучения закономерностей формирования динамических свойств виброза-щитных систем с учетом особенностей объектов защиты, совершающих движения определенного типа, разработан метод построения математических моделей, в рамках которого возможна оценка способов и средств изменения динамического состояния динамических систем. Суть метода заключается в том, что механическая колебательная система, имеющая в своем составе механизм, интерпретируется структурной схемой-аналогом, в которой механизм представляется дополнительной обратной связью в виде дифференцирующего звена второго порядка.

Разработаны методологические основы и соответствующая технологическая основа оценки и учета особенностей расположения типовых элементарных звеньев в структуре механических колебательных систем.

Изучены и определены возможности рычажных связей, возникающих при вращательно-качательных движениях объектов защиты в составе виброзащитных систем с одной, двумя и более степенями свободы. На основе результатов исследований предложена методика построения оригинальных конструктивно-технических решений в задачах вибрационной защиты.

Введение и учет возможностей механизмов в структуре механических колебательных систем основаны на представлениях о том, что звенья механизмов совершают только малые упругие колебания относительно положения установившегося статического равновесия. В этом случае введение механизмов в рамках структурной теории виброзащитных систем интерпретируется как введение дополнительных обратных связей по ускорению движения объекта защиты.

Разработана методика определения динамических реакций, возникающих в точках контакта составных элементов колебательных систем между собой, а также в точках взаимодействия с опорными поверхностями. Показано, что такая задача решается как определение параметров обратной связи системы, приведенной к определенному виду. В частности, это связано с представлением объекта защиты от вибрации в виде звена интегрирования второго порядка.

Разработаны методы динамического синтеза виброзащитных систем, содержащих в своем составе различные механизмы. Предложена обобщенная теория рычажных динамических гасителей колебаний оригинальных конструктивных форм.

По результатам теоретических разработок проведены лабораторные испытания на лабораторном макете рычажного динамического гасителя колебаний, которые подтвердили возможности реализации исходных положений теоретического базиса.

Исследования выполнены по гранту в рамках Федеральной целевой программы «Научные и педагогические кадры инновационной России» на 2012 – 2013 гг. по теме «Мехатроника виброзащитных систем» (1.3.2 – Естественные науки) № 14.132.21.1362.