Method for calculating the parameters of superplasticity of titanium alloys based on the results of test forming into a rectangular matrix at constant pressure
Автор: Murzina G.R., Zharmukhametova A.R., Ganieva V.R., Enikeev F.U.
Рубрика: Программирование
Статья в выпуске: 1 т.16, 2023 года.
Бесплатный доступ
We propose a procedure to determine the strain rate sensitivity index of a superplastic material from the results of bulge forming of a long thin rectangular membrane under constant pressure of inertia gas. In contrast to other known procedures, the method suggested takes into consideration the presence of entry radius in the matrix set used. The mathematical model of the technological process is developed based on the main assumptions of the thin shell theory. To validate the procedure suggested the finite element analysis is fulfilled using the software package ANSYS 10 ED. Experimental approbation of the method suggested is carried out on the titanium alloys Ti-6Al-4V, a good agreement is achieved. It is shown that taking into account the influence of the entry radius allows to improve considerably the accuracy for finite element modelling. We draw the conclusion that the procedure developed may be recommended for practical usage to determine the superplastic parameters of thin sheet superplastic materials.
Superplastic forming, rheological parameters, rectangular matrix, entry radius, ansys
Короткий адрес: https://sciup.org/147240861
IDR: 147240861 | УДК: 004.94 | DOI: 10.14529/mmp230108
Текст научной статьи Method for calculating the parameters of superplasticity of titanium alloys based on the results of test forming into a rectangular matrix at constant pressure
Superplastic forming (SPF) is one of the most promising processes for processing sheet materials. Due to the effective use of the advantages of superplastic materials, this method can be used to obtain complex-shaped products of various shapes. The traditional scheme of the SPF process is the shaping of a sheet blank into a matrix cavity under action of gas pressure. Superplastic forming makes it possible to obtain hollow products from a flat or pre-profiled sheet or tubular workpiece due to the action of a small gas-static pressure [1]. Superplastic forming processes have the following advantages over traditional metal forming processes: the ability to obtain parts of complex shape in one pass; relatively low cost of tooling; low capital costs of production equipment [2].
To describe the superplasticity (SP) of materials that deform under optimal SP conditions, the standard power constitutive relation
σ=Kξ m (1)
is used [3], where σ is the flow stress; ξ is the strain rate; K and m are the material constants.
The adequacy of the mathematical models of technological processes of the superplasticity depends on the determination of the superplastic parameters of the material K and m. Traditionally, the method for calculating includes a series of uniaxial tensile tests for standard specimens at different strain rates [4]. In [5], a method is proposed for determining the material constants of the SP based on the results of full-scale experiments consisting of three test formings of hemispheres into a cylindrical matrix. The authors of [6] assessed the accuracy of the models of the SPF process created using the constants of the material determined by different methods. It is shown that when determining the superplastic parameters of the material K and m from full-scale experiments, agreement between the simulation results and experiment acceptable for engineering calculations is achieved. Also, the issues of determining the superplastic parameters of the material K and m are considered in [7–9].
The aim of this work is to determine the superplastic parameters of titanium alloys based on the results of forming thin-sheet materials into a rectangular matrix taking into account the input radius of the matrix at constant pressure.
1. Problem Statement
Deformation of an extended rectangular membrane is often used as a calculation scheme in the analysis of the processes of superplastic forming of sheet materials into a rectangular matrix [10–12]. Consider the deformation process of a sheet blank with the initial thickness s 0 into a rectangular matrix with the depth D , the width 2W and the length L (Fig. 1).
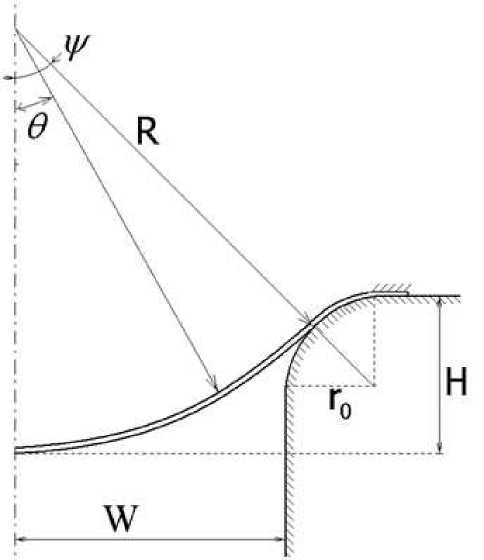
Fig. 1 . Scheme of deformation of sheet into a rectangular matrix
The following geometric relations are satisfied:
W + ro = (R + ro) sin2,
H = (W + ro) • tg 2,
R = -W [1 + ^0 •(1 - sin 2)1- sinψ W
The work [13] presents experimental data on the results of forming extended rectangular membranes from the titanium alloy Ti-6Al-4V. However, the authors of [13]
do not take into account the entry radius of the matrix while determining the rheological parameters.
Assume that the initial sheet is thin ( so ^ W ), the membrane is long enough ( W ^ L ), and the material is incompressible. Assume that there is a sufficiently good lubricant at the contact of the deformable sheet with the matrix in the zone of the entry radius r o in order to accept the condition of free slipping of the sheet along the matrix. In the average (along the length L of the matrix) section, a plane strain condition is realized, in which only two components of the strain rate tensor are nonzero: the circumferential ξ t and the normal C n , and the condition of incompressibility in velocities involves C t + C n = 0 , whence C t = C n = - (1/s) • ds/dt , where t is time.
Repeating the reasoning given in the book [12], we draw the conclusion that the middle surface of the membrane during its deformation is a part of the surface of a circular cylinder with a certain opening angle 2ψ . In this case, if the edge effect is neglected, we can conclude that if the thickness of the membrane before deformation is constant, then it remains the same at all points of the dome and throughout the entire forming process. Considering this circumstance, the incompressibility condition can be written as so • (W + ro) = s(R + ro)^, whence, taking into account
W + ro = (R + ro) sin |, we arrive at
/ sin |A s=4
Thus, at any moment of time, the shell thickness is constant along its profile and is determined by the value of ψ . By virtue of the accepted assumption about the free sliding of the sheet along the matrix, a similar statement is also true for that part of the shell that is in contact with the matrix in the zone of the entry radius.
Differentiating with respect to time, we obtain that the expression for the shell thickness is
Cn = (s) • (T) = - (I -ctg I)(#) ■
Taking into account that each fiber of the length W + r o in the initial state is stretched by ( R + r o ) ( R + ^ 0 ) w times, the circumferential strain rate C t is equal to
Ci=(d1) • (I -ctg *)■
From incompressibility, ξ t + ξ n = 0. Therefore,
Cn = -Ct = - (d1) • (I- ctg *) ■
The remaining components of the strain rate tensor are equal to zero. The strain rate intensity ξ e is equal to
C = 12£jj ] 2 = 5 = (;2|)(d1 )•( I —)■ where ξij are the components of the strain rate tensor, among which only two components are nonzero: ξt and ξn . There are the basic equations of the thin shell theory. In this case,
|
they take the form: |
σ z + σ t = p, (12) ρ z ρ t s pρ t σ z = 2s . (13) |
Then, taking into account that in this case ρ z = ∞ and
|
P t = R = (• /У [1+ ( ) " (1 sin ^)1, sin ψ W |
(14) |
|
pR pW r0 σ t = s = s sinψ · 1+ W · (1 - sinψ) , |
(15) |
|
pR pW r0 σ z = 2 s =2 s sinψ · 1+ W · (1 - sinψ) |
(16) |
|
or, given |
|
|
sin ψ s = s0 ψ , |
(17) |
|
T1 = pR = _W_ = pW » Г + / ) • (1 - sin ^1 , s s sin ψ s0 sin 2 ψ W |
(18) |
|
pR pW pW ψ r0 σ z = 2 s =2 s sinψ=2 s 0 sin2 ψ 1+ W (1 - sinψ) . |
(19) |
|
2. Mathematical Model |
Consider the following relations for the strain rate intensity and stress intensity:
2 dψ 1
ξ e = √ 3 · dt · Ψ - ctgψ ,
3 · pW · ψ · 1+r 0 · (1 - sinψ) .
2 s0 sin 2 ψ W
Substitute relations (20) and (21) into the basic ratio of Backofen model (1):
m r0 mtm 2 d^ ( 1
1+ W · (1 - sinψ) =Kξ = √ 3 · dt · Ψ - ctgψ . (22)
Rewrite the resulting expression (22) in the following form:
(Z)"(£)-=(-)4i - I- 1 , ' ,- (У-(23)
1 + W r 0 (1 - sinψ)
where n = 1 . m
Consider the deformation mode at a constant gas pressure forming p = p 0 = const. Represent the main differential equation of the geometric model in the form
( 1 + (W) (1 - ndψ. (24) sin ^) Integrating both parts of the equation, we obtain the expression ( ^'(KW )'-F^ where Fm(^) is a special function of two variables defined by the expression -^n^Xi 1 + (W) (1 - ndx. sin ^) The prime at F is used to separate function (26) from function (27) corresponding to a matrix with the entry radius r0= 0: - x) dx. From equation (25), the forming time at constant gas pressure can be calculated by the formula * = (^W* «• (28) To determine the value of the index of sensitivity to the strain rate m, we use the formula proposed in the paper [5]: K = ^ i 2 piW s0 ( i3t Г 2Fm (^)) 1 where i = 1, 2. The final equation for calculating the parameter K is as follows: K = K1 + ^2 .
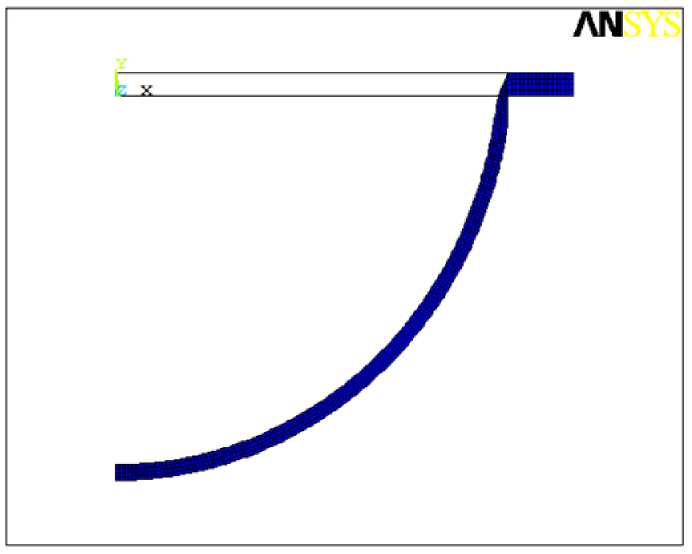
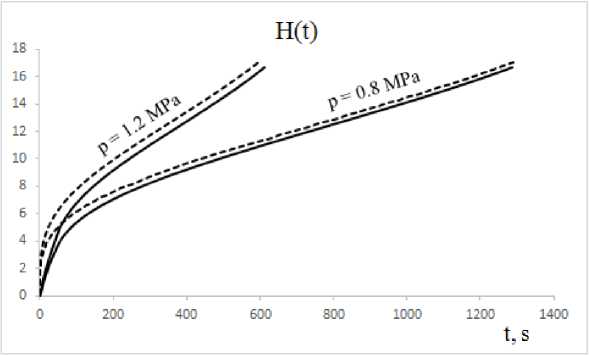
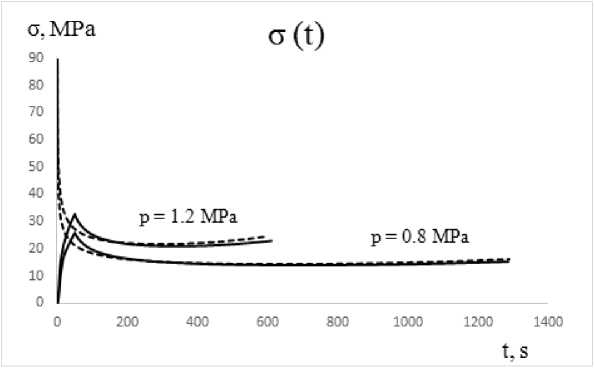
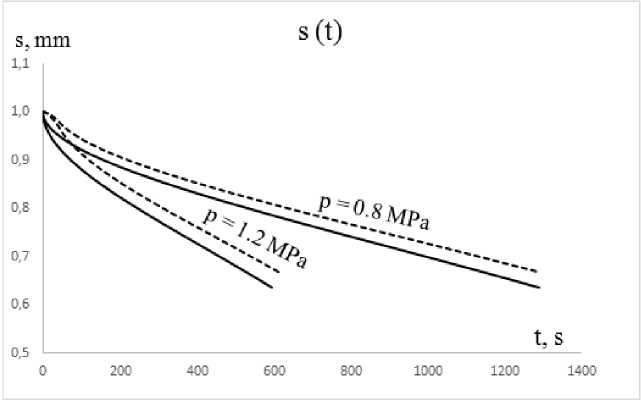
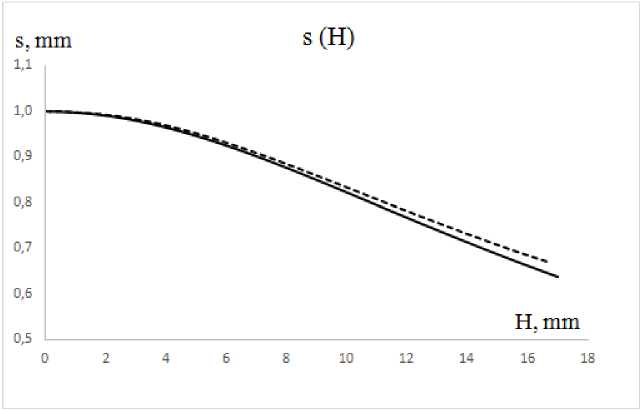
3. Analysis Consider superplastic forming of an extended rectangular membrane made of Ti-6Al-4V titanium alloy of the thickness s0= 1 mm, the width 2W = 30 mm and the entry radius r0= 0 mm and r0= 2 mm into a rectangular matrix at a constant gas pressure under the temperature T = 900°C [14], using the rheological parameters K and m calculated analytically. Deformation of an extended rectangular membrane is modeled using the ANSYS 10 ED software package, in which the boundary value problem of creep theory is solved. For r0= 2 mm, the values of the material constants m = 0,522831 and K = 964,034 MPa·smare calculated for the minimum set of initial data at 0,8 and 1,2 MPa. Therefore, in the ANSYS 10 ED calculations, we assume: C2= n = 1/m = 1,9127, C1 = 1/Kn = 6, 5532 • 10-18s-1Pa~n, the values of the elastic constants are chosen as E = 1, 0 · 1010P a, ν = 0,35. Fig. 2 shows the finite element mesh at the initial and final stages of modelling, taking into account the entry radius of the matrix r0 = 2 mm. Fig. 2. Finite element mesh taking into account the entry radius of the matrix Analytically, using the minimum set of initial data at gas pressures of 0.8 and 1.2 MPa, for r0 = 0 mm, the following values of the material constants are calculated: m = 0,522831 and K = 948,6 MPa·sm. Therefore, in the calculations we assume that C2 = n = 1/m = 1, 9127, C1 = 1/Kn= 6, 7586 • 10-18s-1Pa-n. To prove the influence of the entry radius on the accuracy of calculations, we also perform a calculation in ANSYS with a zero entry radius. Fig. 3 shows the finite element mesh at the initial and final stages of modelling, without taking into account the entry radius of the matrix r0 = 0 mm. The results of finite element modelling of superplastic forming into a rectangular matrix with the entry radius r0 = 0 mm and r0 = 2 mm are compared with the corresponding experimental data for the Ti-6Al-4V alloy. The results obtained are shown in Table 1 and Table 2, respectively. For r0= 0 mm, the modelling accuracy does not exceed 43%, as shown in Table 1, however, for r0 = 2 mm, the modelling accuracy does not exceed 15%, as shown in Table 2. Thus, taking into account the entry radius into the rectangular matrix, we improve the calculation results. Fig. 3. Finite element mesh without taking into account the entry radius of the matrix Table 1 Duration of forming into a rectangular matrix with the entry radius of 0 mm at constant pressure Pressure (MPa) Forming time (s) Accuracy of modelling (%) Exp.[31] FEM 0.8 1290 737 42,9 1.2 594 359 39,6 Table 2 Duration of forming into a rectangular matrix with the entry radius of 2 mm at constant pressure Pressure (MPa) Forming time (s) Accuracy of modelling (%) Exp.[31] FEM 0.8 1290 1106 14,3 1.2 594 527 11,3 For graphical representation, it is also necessary to compare the data using graphs (Figs. 4–7), where solid lines are FEM solutions, dashed lines are analytical solutions. Time dependencies of the dome height H (Fig. 4) for SPF at constant gas pressure p (indicated by numbers near the curves) and time dependencies of the stress intensity σ (MPa) (Fig. 5) are calculated analytically and using the finite element method. Fig. 4. Dependence of the height of the dome on time, H (mm) Fig. 5. Time dependencies of the stress intensity σ (MPa) Fig. 6. Time dependencies of the thickness, s (mm) Fig. 7. Dependencies of the thickness on the height, s (mm) As follows from a comparison of the dependencies of the height of the dome H and the thickness of the dome s on time, a satisfactory agreement is achieved between the dependencies calculated in ANSYS (solid lines) and the dependencies calculated analytically (dashed lines) SPF at a constant gas pressure p. It was found that the dependence of the dome thickness s on the dome height H does not depend on the gas pressure. Conclusions The implemented method to determine the superplastic parameters allows to achieve an acceptable accuracy of finite element modelling in the ANSYS program and may be recommended for practical use when forming thin-sheet titanium materials into a rectangular matrix, taking into account the entry radius at a constant gas pressure. We show the influence of the entry radius into a rectangular matrix, which increases the accuracy of calculations in the ANSYS software from 42,9% to 14,3% at the pressure of 0.8 MPa and from 39,6% to 11,3% at the pressure of 1.2 MPa (Table 1 and Table 2). Acknowledgments. The reported study was funded by RFBR according to the research project № 20-38-90179.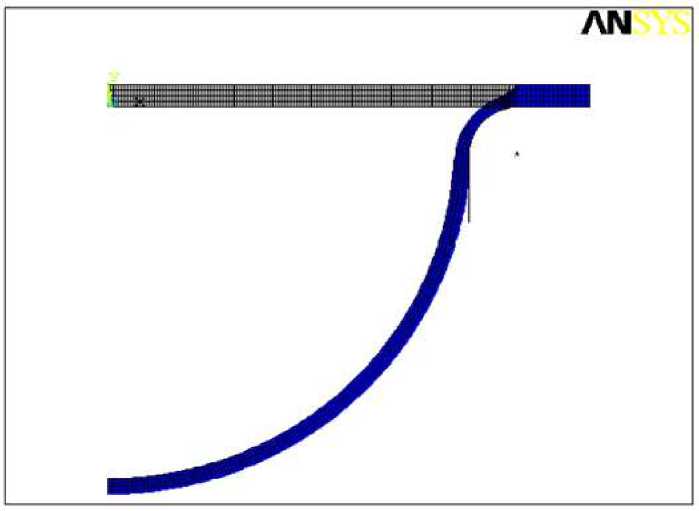
Список литературы Method for calculating the parameters of superplasticity of titanium alloys based on the results of test forming into a rectangular matrix at constant pressure
- Perez-Prado M.T., Kassner M.E. Fundamentals of Creep in Metals and Alloys. Amsterdam, Elsevier Science, 2015.
- Smirnov O.M. Obrabotka metallov v sostoyanii sverkhplastichnosti [Superplastic Metal Working Techniques]. Moscow, Mashinostroenie, 1979. (in Russian)
- Safiullin R.V., Vasin R.A., Enikeev F.U. Determination of the Parameters of Superplastic Forming for Long Rectangular thin Sheet Titanium Alloy Ti-6Al-4V. Acta Metallurgica Sinica, 2000, vol. 13, pp. 567-573.
- Kaibyshev O.A. Sverkhplastichnost' promyshlennykh splavov. [Superplasticity of Industrial Alloys]. Moscow, Metallurgy, 1984. (in Russian)
- Enikeev F.U., Kruglov A.A. An Analysis of the Superplastic Forming of a Thin Circular Diaphragm. International Journal of Mechanical Sciences, 1995, vol. 37, no. 5, pp. 473-483.
- Vasin R.A., Enikeev F.U., Kruglov A.A., Safiullin R.V. [Identification of Defining Relations According to the Results of Technological Experiments]. Mechanics of Solids, 2003, no. 2, pp. 111-123. (in Russian)
- Aksenov S.A., Chumachenko E.N., Kolesnikov A.V., Osipov S.A. Determination of Optimal Gas Forming Conditions from Free Bulging Tests at Constant Pressure. Journal of Materials Processing Technology, 2015, pp. 158-164.
- Jarrar F.S., Abu-Farha F.K., Hector L G., Khraisheh M.K. Simulation of High-Temperature AA5083 Bulge Forming with a Hardening/Softening Material Model. Journal of Materials Engineering and Performance, 2009, vol. 18, no. 7, pp. 863-870. DOI: 10.1007/ s11665-008-9322-5
- Carrino L., Giuliano G., Palmieri C. On the Optimization of Superplastic Forming Processes by the Finite-Element Method. Journal of Materials Processing Technology, 2003, vol. 143144, pp. 373-377. DOI: 10.1016/S0924-0136(03)00423-0
- Malinin N.N., Romanov K.I. [An Investigation of the Process of Gasostatic Forming of a Long Membrane]. Soviet Machine Science, 1982, no. 4, pp. 98-101. (in Russian)
- Ghosh A.K., Hamilton C.H. Influence of Material Parameters and Microstructure on Superplastic Forming. Metallurgical Transactions, 1982, vol. 13, no. 5, pp. 733-743.
- Malinin N.N. Polzuchest v obrabotke metallov [Creep in Metal Working]. Moscow, Mashinostroenie, 1986. (in Russian)
- Ganieva V.R., Kutlueva A.I., Enikeev F.U. Method to Determine the Optimal Conditions for Superplastic Flow. Problems of Mechanical Engineering and Automation, 2012, no. 1, pp. 132-138. (in Russian)
- Safiullin R.V., Enikeev F.U. Calculation of Regimes for Superplastic Forming of an Elongated Rectangular Membrane. Forging and Stamping Production. Material Working by Pressure, 2001, no. 3, pp. 35-40. (in Russian)


